半透明物体のレンダリングモデルをまとめてみた
こんにちはtatsyです。
今回の記事はレイトレ合宿4!?のアドベントカレンダー第8週目の記事です。そのほかの記事につきましても、レイトレ合宿4!?のページからご覧いただけますので、ご興味のある方はぜひぜひ読んでみてください。
さて、今回の記事の内容についてですが、レンダリングにおける半透明物体の扱い方について、dipoleモデルとその発展系を中心として、いくつかの手法をご紹介したいと思います。
レンダリングにおける半透明物体
CGにおいて、おそらくもっとも重要と思われる半透明物体は人間の肌だと思います。このほかにも世の中に存在する多くの物体 (例えば、人間以外の動物の肌や、植物の繊維など) も厳密には表面下に光を透過する性質を持っています。
このような物体の表面下に光が浸透して、物体内で光が散乱、吸収される光学的現象のことを表面下散乱と呼びます。この現象により、物体に透明感が生まれ、リアルな印象を与えるようになります。
試しに、石膏像のような物体を透明感の有り、無しでレンダリングしたものが以下の画像になります。
 |  |
この画像の場合には、特にどちらが正しいというものは特にないのですが、右側の画像の方が透明感があるのが確認できると思います。
半透明の物体をリアルにレンダリングするためには、光が物体の中で吸収されたり、散乱されたりするのを真面目にあつかうボリュームレンダリングが厳密で良いのですが、その真面目さ故に計算時間が膨大というのがボリュームレンダリングの難点です。
そこで、実際に半透明物体をレンダリングする時には、レンダリング対象の物体がどういう光学的性質を持つのかについて、適切な近似を使うのが一般的です。
特に、人間の肌などの内部で拡散が多く起こるような物質に対しての近似法はとてもたくさん研究されています。今回は、その近似法の親玉でもあるdipoleモデルを中心に、その発展系をいくつかご紹介したいと思います。
拡散近似法 (Diffusion Approximation)
まず、実際の近似法に行く前に、これから紹介する方法の元になっている拡散近似法という理論を、ものすごく大雑把に説明したいと思います(間違ってたらきっと誰かが教えてくれる)。
拡散近似法は半透明物体、より一般的には物体内部で拡散を引きおこす媒質を対象としています。このような物体の内部にある1点$\vec{\omega}$から入射してくる光の強さを以下のように表します。
$$ \displaystyle L(x, \vec{\omega}) = \frac{1}{4 \pi} \phi(x) + \frac{3}{4 \pi} \vec{\omega} \cdot \vec{E}(x) $$
この式で、$x$に入射してくる光エネルギーの方向的な偏りを表現した項になります。
この式は拡散近似法という名前の通り、近似的な計算モデルです。実際には、厳密な計算モデルの式を球面調和関数で1次の項まで展開したものと解釈できます。
この方程式において、左辺の$\phi(x)$に関する微分方程式になっています。
この微分方程式に対して、境界面が平らであり、その平らな境界面から見た片側に無限に半透明の媒質が広がっているという境界条件を課すと、この微分方程式を解くことができます。詳細の説明は省略しますが、この解は以下のような式になります。
$$
\displaystyle \phi(x) = \frac{1}{4 \pi D} \frac{e^{-\sigma_tr} r(x)}{r(x)}
$$
この微分方程式の解$x$に到達する光エネルギーの強さを表すことになります。この形は、以下で紹介するdipoleモデルの基礎となっている式ですので、式の形だけでも覚えておいてください。
Dipoleモデル
レンダリングにおいて良く用いられる多重散乱光の近似式にdipoleモデル 1と呼ばれるものがあります。このモデルは、拡散近似法の場合と同様に平面的な境界面を持つ無限に広がった半透明媒質を対象としています。
Dipoleモデルでは、物体の中を取って再び外に出てくる光の寄与を2つの仮想的な光源からの影響の和で近似します。片方の仮想光源は半透明媒質の中に、もう一方の仮想光源は半透明媒質の外に置きます。通常、物体に侵入すると光は物体の内側を通るので、物体内部に置いた仮想光源にはrealを表す添え字rが、物体外部に置いた仮想光源にはvirtualを表す添え字vが使われることが多いです。
多重散乱が支配的である場合には、物体中での光の減衰を光の入射位置から出射位置までの距離の関数としてあらわせることが知られていて、その関数を拡散反射関数といい$R_d(r)$で表します。入射点と出射点でFresnel反射/透過による光エネルギー量の変化を考慮すると、半透明物体中を進む光エネルギーの変化が以下の式により表せます。
$$ \displaystyle S_d(x_i, \vec{\omega}_i ; x_o, \vec{\omega}) = \frac{1}{\pi} F_t(\eta, \vec{\omega}_i) R_d(| x_i - x_o |) F_t(\eta, \vec{\omega}_o) $$
Dipoleモデルでは、この式中の拡散反射関数$R_d(r)$を次のように表します。
$$ \displaystyle R_d(r) = \frac{\alpha’}{4 \pi} \left[ z_r (d_r + 1) \frac{e^{-\sigma_{tr} d_r}}{d_r^3} - z_v (d_v + 1) \frac{e^{-\sigma_{tr} d_v}}{d_v^3} \right] $$
と、この式を見ると、最初はかなり面食らうわけですが、これは拡散近似法のところで述べた微分方程式の解を仮想的な2つの光源について足し合わせたものと考えることができます。なお、後ろ側の項が和であるにも関わらずマイナスの係数となっているのは距離をマイナス方向に取っているためです。
実際にdipoleモデルを計算するプログラムをPythonで組んでみたものが以下のようになります。
class Dipole(object):
def __init__(self, sigmap_s, sigma_a, eta):
A = (1.0 + self.Fdr(eta)) / (1.0 - self.Fdr(eta))
self.sigmap_t = sigma_a + sigmap_s
self.sigma_tr = Color.sqrt(3.0 * sigma_a * self.sigmap_t)
self.alphap = sigmap_s / self.sigmap_t
self.zpos = Color(1.0, 1.0, 1.0) / self.sigmap_t
self.zneg = -self.zpos * (1.0 + (4.0 / 3.0) * A)
def Rd(self, r):
r2 = r * r
dpos = Color.sqrt(Color(r2, r2, r2) + self.zpos * self.zpos)
dneg = Color.sqrt(Color(r2, r2, r2) + self.zneg * self.zneg)
ret = (self.alphap / (4.0 * math.pi)) * \
((self.zpos * (dpos * self.sigma_tr + Color(1.0, 1.0, 1.0)) * \
Color.exp(-self.sigma_tr * dpos)) / (dpos * dpos * dpos) - \
(self.zneg * (dneg * self.sigma_tr + Color(1.0, 1.0, 1.0)) * \
Color.exp(-self.sigma_tr * dneg)) / (dneg * dneg * dneg))
return ret
def Fdr(self, eta):
if eta >= 1.0:
return -1.4399 / (eta * eta) + 0.7099 / eta + 0.6681 + \
0.0636 * eta
else:
return -0.4399 + 0.7099 / eta - 0.3319 / (eta * eta) + \
0.0636 / (eta * eta * eta)
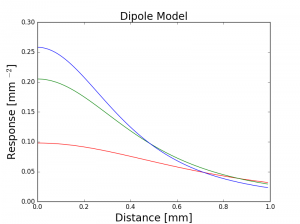
実際に、このプログラムを使ってJensen et al. 2001のSkin2モデルをプロットしてみると、次のような結果を得ることができました。
Multipoleモデル
Multipoleモデル [2]はdipoleモデルを拡張したもので、dipoleの時に2つしかとっていなかった仮想の光源を複数に増やしたものです。
Mulitpoleモデルが扱おうとしているものは特定の厚みを持った半透明媒質の層です。dipoleモデルで扱っていた半無限の物体とは違い、層状になっているものの場合には境界面が上下に2つあるので、その2つの境界面における境界条件を扱うために仮想的な光源を複数にしています。厳密にはこの仮想光源は無限に取らないといけないのですが、実用上はそれほどたくさん取らなくても大丈夫です。
式自体はdipoleモデルとそれほど変わりませんので、元の論文であるDonner and Jensen 2005、あるいは下に示すソースコードを確認してください。
class Multipole(object):
def __init__(self, sigmap_s, sigma_a, eta, d=0.1, n=2):
A = (1.0 + self.Fdr(eta)) / (1.0 - self.Fdr(eta))
self.sigmap_t = sigma_a + sigmap_s
self.sigma_tr = Color.sqrt(3.0 * sigma_a * self.sigmap_t)
self.alphap = sigmap_s / self.sigmap_t
self.l = Color(1.0, 1.0, 1.0) / self.sigmap_t
self.zb = self.l * (2.0 / 3.0) * A
self.d = d
self.n = n
def Rd(self, r):
ret = Color(0.0, 0.0, 0.0)
for i in range(-self.n, self.n+1):
zr = 2.0 * i * (Color(self.d, self.d, self.d) + 2.0 * self.zb) + self.l
zv = 2.0 * i * (Color(self.d, self.d, self.d) + 2.0 * self.zb) - self.l - 2.0 * self.zb
r2 = r * r
dr = Color.sqrt(Color(r2, r2, r2) + zr * zr)
dv = Color.sqrt(Color(r2, r2, r2) + zv * zv)
ret += (self.alphap / (4.0 * math.pi)) * \
((zr * (dr * self.sigma_tr + Color(1.0, 1.0, 1.0)) * \
Color.exp(-self.sigma_tr * dr)) / (dr * dr * dr) - \
(zv * (dv * self.sigma_tr + Color(1.0, 1.0, 1.0)) * \
Color.exp(-self.sigma_tr * dv)) / (dv * dv * dv))
return ret
dipoleモデルとの比較もかねて、multipoleモデルの値をプロットすると以下の画像のようになります。multipoleモデルは実線で、dipoleモデルは点線でプロットしてあります。multipoleモデルで扱ったのはJensen et al. 2001のskin2のデータで、厚みは左から1mm, 5mm, 10mmになっています。
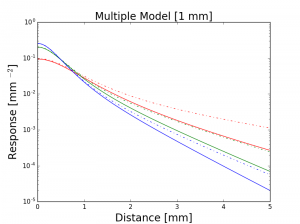 | 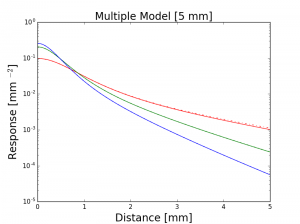 | 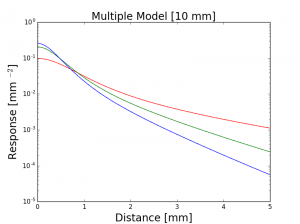 |
y軸が対数になっていますが、見ての通り、厚みが小さいときには、multipoleの方が小さめの値を取ることが分かります。これは、層が薄い時には、反対側に透過していく光の成分が出てくるためだと思います。一方で、層が厚くなって、半無限に媒質が広がるという仮定に近づくとdipoleもmultipoleもとても近い値をとることが分かります。理論的にはmultipoleモデルで$d=\infty$のときにはdipoleモデルと等価になります。
最後にひとつ補足というか、私のした勘違いですが、Multipoleの論文を読むと仮想光源の数を$n$と層の数が関係しているのかなと思ってしまいました。
ですが、最初に述べた通り仮想光源を複数おくのは上下の境界面における境界条件を正しく扱うためですので、仮想光源の数と層の数とは基本的に関係ありません。
Quantized diffusionモデル
ここまでの2つのモデルでは拡散近似法における平均入射照度$\phi(x)$に次の式を使っていました。
$$ \displaystyle \phi(x) = \frac{\Phi}{4 \pi D} \frac{e^{-\sigma_{tr} r(x)}}{r(x)} $$
この式をよく見ると$r$がゼロに近い場合には大きめの値を取らなければおかしいということになります。
そこでquantized diffusion [4]モデルでは、拡散近似法で用いていた式とは異なるGrosjeanの近似と呼ばれる方法を使っています。この近似法を使うと$\phi(x)$が、
$$ \displaystyle \phi(x) = \frac{e^{-\sigma_t r(x)}}{4 \pi r(x)^2} + \frac{1}{4 \pi} \frac{3 \sigma’_s \sigma’_t}{2 \sigma_a + \sigma’_s} \frac{e^{-\sqrt{\frac{\sigma_a}{D}} r(x)}}{r(x)} $$
この式を使うと$r$が小さい場所でも\phi(x)がそれなりの大きさの値を取るようになり、近似を使わない厳密な解にかなり近い値を取るようになります。
Quantilzed diffusionでは、上記の式の第1項をさらに展開します。この第1項は光源から光が出射された時刻による積分の形で表されることが知られているので、この積分を離散化して和の形に書き直します。ここでの離散化がquantized diffusionと呼ばれる所以です。
ここでも詳細な説明は省きますが、この離散化された$R_d$もガウス関数の和のような形になることが示されています。
このようにガウスの和の形で書き表せるということは様々な面で有用で、モンテカルロ・パストレーシングをする場合には関数のサンプリングが簡単になりますし、リアルタイムレンダリングにおいては、Screen-space subsurface scatteringのようにガウスの畳み込み計算をシェーダで高速化することで素早く半透明物体を描画できたりします。
研究の発展の流れからすると、先に肌のレンダリングモデルとして、ガウス関数の足しあわせを使う手法がd’Eon et al. 2007 [3]で発表されていて、d’Eon and Irving 2011で述べられた、このquantized diffusionは2007年の論文を理論的に裏付けたという位置付けとも考えられると思います。
Quantized diffusionと通常のdipoleモデルとの比較に関しては、以下のbetter dipoleモデルを紹介した後で、まとめて比較をしてみたいと思います。
Better dipoleモデル
上記のQuantized diffusionモデルは物理的にかなり正しいのですが、見てもらって分かる通り、和の計算が多く少し計算に時間がかかります。そこでd’Eonさんが2012年に発表したのがbetter dipole [5]というモデルです。
式自体はdipoleとあまり変わらず、計算も軽いのですが、光が入射した位置に近い場所でより物理的に正しい値をとるようになります。
式の内容はともかく、実装はとても簡単です。例のごとくPythonで実装してみたものが以下のコードになります。
class BetterDipole(object):
def __init__(self, sigmap_s, sigma_a, eta):
self.sigmap_t = sigmap_s + sigma_a
self.alphap = sigmap_s / self.sigmap_t
self.eta = eta
self.A = (1.0 + 3.0 * self.C2(eta)) / (1.0 - 2.0 * self.C1(eta))
self.D = (2.0 * sigma_a + sigmap_s) / (3.0 * self.sigmap_t * self.sigmap_t)
self.sigma_tr = Color.sqrt(sigma_a / self.D)
self.zr = Color.ones() / self.sigmap_t
self.zb = 2.0 * self.A * self.D
self.zv = -self.zr - 2.0 * self.zb
self.Cphi = Color.ones() * (0.25 * (1.0 - 2.0 * self.C1(eta)))
self.CE = Color.ones() * (0.50 * (1.0 - 3.0 * self.C2(eta)))
def Rd(self, r):
r2 = r * r
dr = Color.sqrt(Color.ones() * r2 + self.zr * self.zr)
dv = Color.sqrt(Color.ones() * r2 + self.zv * self.zv)
ar = self.zr * (self.sigma_tr * dr + Color.ones()) / (dr * dr)
av = self.zv * (self.sigma_tr * dv + Color.ones()) / (dv * dv)
br = Color.exp(-self.sigma_tr * dr) / dr
bv = Color.exp(-self.sigma_tr * dv) / dv
return (self.alphap * self.alphap / (4.0 * math.pi)) * \
((self.CE * ar + self.Cphi / self.D) * br - \
(self.CE * av + self.Cphi / self.D) * bv) / \
(1.0 - self.C2(1.0 / self.eta))
def C1(self, eta):
eta2 = eta * eta
eta3 = eta2 * eta
eta4 = eta3 * eta
eta5 = eta4 * eta
if eta < 1.0:
return (0.919317 - 3.4793 * eta + 6.75335 * eta2 \
-7.80989 * eta3 + 4.98554 * eta4 - 1.36881 * eta5) / 2.0
else:
return (-9.23372 + 22.2272 * eta - 20.9292 * eta2 + 10.2291 * eta3 \
- 2.54396 * eta4 + 0.254913 * eta5) / 2.0
def C2(self, eta):
eta2 = eta * eta
eta3 = eta2 * eta
eta4 = eta3 * eta
eta5 = eta4 * eta
if eta < 1.0:
return (0.828421 - 2.62051 * eta + 3.36231 * eta2 - 1.95284 * eta3 \
+ 0.236494 * eta4 + 0.145787 * eta5) / 3.0
else:
return (-1641.1 + 135.926 / eta3 - 656.175 / eta2 + 1376.53 / eta \
+ 1213.67 * eta - 568.556 * eta2 + 164.798 * eta3 \
- 27.0181 * eta4 + 1.91826 * eta5) / 3.0
Better dipoleとquantized diffusionをdipoleモデルと比較してみます。今回の比較では$2 \pi r$をつけて比較をします。これは、半径が大きい場所での誤差を相対的に目立たせるためです。
今回の比較ではquantized diffusionとbetter dipoleに加えて、モンテカルロ法で作ったデータも比較に加えました。ただ、いろいろ試した結果、quantized diffusionとモンテカルロ法の結果については、ややズレがあるようで、どこかに間違いがありそうです。どうか、参考程度にご覧下さい。
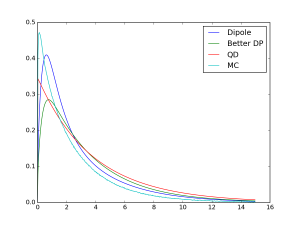 | 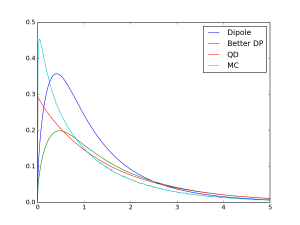 |
| $\sigma_a=0.1, \eta=1.5$ | $\sigma_a=0.5, \eta=1.5$ |
こちらの図を見ていただくと、quantized diffusionは、モンテカルロ法のものに比較的近く、better dipoleに関しても、$\sigma_a$が大きいときには他の二つとは離れた値を取っていることがわかります。実際、dipoleモデルは吸収がよく起こるような媒質の場合にはそれほど良い近似を与えないようです。
今回の比較に使ったコードはGitHubにまとめてありますので、こちらも参考程度にご覧いただければ幸いです。
https://github.com/tatsy/DiffusionApprox
その他のモデル
この他にも半透明物体を扱うためのモデルはいくつかあって、Empirical BSSRDF [6]のように、半透明物体モデルをモンテカルロ法で前計算するものや、入射光の向きによる影響を考慮できるようにdipoleモデルを改良したdirectional dipole [7]というモデルなどもあります。今回は私の勉強不足でご紹介できませんでしたが、ご興味のある方は、ぜひご覧下さい。
実際にレイトレするには?
ここまでに紹介した方法を使って、実際にレイトレをするためには、Jensen and Burder 2002 [8]の階層的積分法 (Hierarchical Integraion) という方法がよく使われます。
この方法はあらかじめ半透明物体の表面にサンプル点をばらまいておいて、そのサンプル点における入射光の放射照度を使って物体表面上の任意の点における透過光を計算するという方法を八分木構造を使って高速化したものです。
MitsubaレンダラーのSubsurfaceマテリアルでは、この階層的積分法が使われています。PBRTにも、バージョン2には実装があったのですが、バージョン3では何らかの理由で無くなってしまったようです。
まとめ
今回はdipoleモデルを中心に半透明物体のレンダリングモデルについて紹介しました。今回は主にレイトレ的な視点に立った解説でしたが、ガウス関数の和で$R_d(r)$を近似するというあたりの話は、リアルタイムレンダリングにおける、Screen-space subsurface scattering [9]やその発展系であるSeparable subsurface scattering [10]等にもつながる大事な考え方だと思います。
本当は、実際にレイトレした画像の比較や、リアルタイム系の話も盛り込みたかったのですが、今回はこの辺りでお許しをいただければと思います。
今回の記事の記述に関しては、自分もまだしっかり理解できていない部分があるかもしれませんので、もし何か間違い等を見つけられた方がいらっしゃいましたら、ご教授をいただければ幸いです。
それでは、最後までお読みいただきありがとうございました。
参考文献
1 H.W. Jensen et al., “A Practical Model for Subsurface Light Transport”, Proc. of SIGGRAPH 2001.
[2] C. Donner and H.W. Jensen, “Light Diffusion in Translucent Multi-layered Materials”, ACM Trans. Graph., 2005.
[3] E. d’Eon et al., “Efficient Rendering of Human Skin”, Eurographics Symposium on Rendering, 2007.
[4] E. d’Eon and G. Irving, “A Quantized-Diffusion Model for Rendering Translucent Materials”, ACM Trans. Graph., 2011.
[5] E. d’Eon, “A Better Dipole”, Technical Report, 2012.
[6] C. Donner et al., “Empirical BSSRDF”, ACM Trans. Graph., 2009.
[7] J.R. Frisvad et al., “Directional Dipole for Subsurface Scattering in Translucent Materials”, ACM Trans. Graph., 2013.
[8] H.W. Jensen and J. Buhler, “A Rapid Hierarchical Rendering Technique for Translucent Materials”, ACM Trans. Graph., 2002.
[9] J. Jimenez and D. Guitierrez, “Screen-Space Subsurface Scattering”, in GPU Pro3, 2010.
[10] J. Jimenez et al., “Separable Subsurface Scattering”, Computer Graphics Forum, 2015.