Normalizing Flow入門 第2回 Planar Flow

こんにちはtatsyです。今回も前回に引き続きNormalizing Flowの技術について紹介します。

前回はNormalizing Flowの応用例の一つである変分推論を取り上げて、Normalizing Flowがどのように応用しうるのかについて紹介しました。

今回はこのような応用で用いるためにNormalizing Flowが満たすべき条件について議論し、最も基礎的なNormalizing Flowの一つであるPlanar Flowについて紹介します。

Normalizing Flowの基礎

今回からは、変数を明示的にベクトル表示して$\mathbf{y}$, $\mathbf{z}$という表記を用います。

前回の記事では、Normalizing Flowが簡単に評価可能な確率密度関数$p_Z(\mathbf{z})$と複雑だが有用な確率密度関数$p_Y(\mathbf{y})$の間の変数変換を行うものであることを述べました。

またNormalizing Flowは複雑な確率密度に従う確率変数$\mathbf{y}$を、より単純でサンプルしやすい確率密度に従う確率変数$\mathbf{z}$へと変数変換する、言い換えればnormalizeする関数なのでした。

そこで$\mathbf{y}$から$\mathbf{z}$への変数変換を$\mathbf{z} = \mathbf{f}(\mathbf{y})$と表すと、$p_Y(\mathbf{y})$は次のように表せます。

$$ p_Y(\mathbf{y}) = p_Z(\mathbf{z}) \left| \frac{\partial \mathbf{f}}{\partial \mathbf{y}} \right| $$

なお、式中の偏微分$\partial \mathbf{f} / \partial \mathbf{y}$は変数変換に関するヤコビアンを表します。

Normalizing Flowが満たすべき条件

Normalizing Flowにおいては、上記の変数変換に使う関数$\mathbf{f}$をニューラルネットで表します。そこで、ニューラルネットのパラメータを$\theta$とし、関数を$\mathbf{f}(\mathbf{y}; \theta)$と書き直します。

前回の記事では、Normalizing Flowの変分推論への応用について述べましたが、この応用では、

$$ \begin{equation} \mathbb{E}_{\mathbf{z} \sim p_Z(\mathbf{z})} [ \log p(\mathbf{x}, \mathbf{g}(\mathbf{z}; \theta)) - \log p_Z(\mathbf{z}) ] \label{eq:energy-function} \end{equation} $$

をエネルギー関数として、これを最大化するような問題を解くのでした。この場合、関数$\mathbf{f}$は以下のような性質を満たす必要があります。

1. 関数$\mathbf{f}$が逆行列を持つ (可逆である)
2. 関数$\mathbf{f}$が適度に複雑であり、元の分布$p_Z(z)$を十分に変形できる (表現力が高い)
3. ヤコビアンの計算を含め、関数$\mathbf{f}$の計算が効率的に行える (計算効率が高い)

1つ目の性質は、式\eqref{eq:energy-function}において、逆関数$\mathbf{g}$を評価するために必要な性質になります。

2つ目の性質は$\mathbf{y}$が、そもそも複雑な確率密度分布に従うという前提があるので、より目的に添った変数変換を実現するために必要な性質になります。

3つ目の性質は、変分推論によって変数$\mathbf{x}$を得るために関数$\mathbf{g}$が効率的に評価できる必要があります。また、ニューラルネットの訓練においては、式\eqref{eq:energy-function}を$\theta$で微分すると、その中に$\mathbf{g}$の微分、すなわちヤコビアンの行列式が現れるので、これを効率的に評価できる必要があります。

Normalizing Flowでは、上記の性質を満たす関数$\mathbf{f}_i$を用いて、目的の変数変換を、それらの合成で定義します。

$$ \mathbf{f} = \mathbf{f}_1 \circ \mathbf{f}_2 \circ \cdots \circ \mathbf{f}_N $$

各$\mathbf{f}_i$は逆写像を持つので、$\mathbf{g} = \mathbf{f}^{-1}$についても同様に

$$ \mathbf{g} = \mathbf{f}^{-1} = \mathbf{f}_{N}^{-1} \circ \cdots \circ \mathbf{f}_1^{-1} $$

が成り立ちます。

以後、各$\mathbf{f}_i$ないし$\mathbf{g}_i$をどのように表すかが、Normalizing Flowの性質を決める上で重要となります。

Planar Flow

上記の条件を満たすFlowの一種として、最初にPlanar Flowを紹介します。Planar FlowはNormalizing Flowの最初期の論文であるRezendeらの研究[1]で紹介されたFlowで、関数$f$が以下のように定義されます。

同時期に発表された最初期のNormalizing FlowであるDinhらのNICE[2]と比べると、理論的には少し複雑ですが、その分、考え方はとても面白いです。

Planar Flowでは、変数変換の関数$\mathbf{g}$を以下の式で定義します。

$$ \begin{equation} \mathbf{z} = \mathbf{g}(\mathbf{y}) = \mathbf{y} + \mathbf{u} h(\mathbf{w}^{T} \mathbf{y} + b) \label{eq:planar-flow} \end{equation} $$

ただし、$h$は非線形の関数で、例えばシグモイド関数や双曲線正接(tanh)などが使われるものとします。

この時、変換のパラメータ$\theta$は$\theta = (\mathbf{u}, \mathbf{w}, b)$となります。この式では添字を省略していますが、この定義を各$\mathbf{g}_i$に用いて、より複雑な$\mathbf{g}$を表現することもできます。

評価の計算量は$\mathbf{w}$, $\mathbf{u}$の次元が$D$であるとすると、$\mathbf{g}$の評価に必要な計算は、内積と要素ごとの計算のみなので、その計算量は$\mathcal{O}(D)$となります。

また、$\mathbf{g}$のヤコビ行列の行列式(ヤコビアン)は、以下のように計算されます。

$$ \left| \frac{\partial \mathbf{g}}{\partial \mathbf{y}} \right| = \det \left( \mathbb{1}_{D} + \mathbf{u} h’(\mathbf{w}^{T} \mathbf{y} + b) \mathbf{w}^{T} \right) = 1 + h’(\mathbf{w}^{T} \mathbf{y} + b) \mathbf{u}^{T} \mathbf{w} $$

この式も、元の$\mathbf{g}$と同様、ベクトルの内積と要素ごとの計算が必要な計算になりますので、その計算量は$\mathcal{O}(D)$になります。

Planar Flowは途中に非線形計算を挟んでいるため、複数の$\mathbf{g}_i$を積み重ねることで、十分に複雑な表現が可能であり、また上記の議論から、計算量も$\mathcal{O}(D)$と比較的小さく抑えられていることが分かります。

Planar Flowの可逆性

一方で、Planar Flowは$h$を適切に選ばないと、そのままでは逆関数を持たないので、$h$の選び方には注意が必要です。

Rezendeらの元論文では$h(\mathbf{z}) = \tanh(\mathbf{z})$の場合が紹介されていますので、ここでは、この場合の可逆性について紹介します。

ここでの目標は$\mathbf{z} = \mathbf{g}(\mathbf{y})$として、$\mathbf{z}$から$\mathbf{y}$を求めることなのですが、式\eqref{eq:planar-flow}の逆関数は解析的には求まらないので、ここでは数値的に$\mathbf{z}$から$\mathbf{y}$を求めます。

まずは$\mathbf{y}$を$\mathbf{w} \cdot \mathbf{y}_{\perp} = 0$を満たす$\mathbf{w}$に垂直な成分$\mathbf{y}_{\perp}$と、それ以外の成分$\mathbf{y}_{\parallel} = \mathbf{y} - \mathbf{y}_{\perp}$に分解します。今、$\mathbf{w}_{\parallel}$は$\mathbf{w}$と並行な成分なので、$\mathbf{w}$と適当なスカラー$\alpha \in \mathbb{R}$を用いて、

$$ \mathbf{y}_{\parallel} = \alpha \frac{\mathbf{w}}{\| \mathbf{w} \|^2} $$

と表せるはずです。従って、与えられた$\mathbf{z}$から$\mathbf{y}_{\perp}$ならびに$\alpha$を決定できれば、数値的には$\mathbf{y}$を求めることができます。しかも、$\alpha$が決まれば式\eqref{eq:planar-flow}を変形することで、

$$ \mathbf{y}_{\perp} = \mathbf{z} - \alpha \frac{\mathbf{w}}{\| \mathbf{w} \|^2} - \mathbf{u} h(\alpha + b) $$

から$\mathbf{y}_{\perp}$が求まりますので、実際には$\alpha$だけが求まれば十分です。

ここで、元のPlanar Flowの式\eqref{eq:planar-flow}の両辺に$\mathbf{w}^{T}$を乗ずると、以下の式が得られます。

$$ \begin{aligned} \mathbf{w}^{T} \mathbf{z} &= \mathbf{w}^{T}\mathbf{y} + \mathbf{w}^{T} \mathbf{u} h(\mathbf{w}^T \mathbf{y} + b) \\ &= \alpha + \mathbf{w}^{T} \mathbf{u} h(\alpha + b) \end{aligned} $$

この式の右辺は$\alpha$だけの関数になっていますので、仮に右辺が単調増加する関数ならば、二分法を用いて、数値的に$\mathbf{w}^{T} \mathbf{z}$から$\alpha$を求めることが可能です。

右辺が単調増加する、ということは、その微分が常に0以上になることを意味しますので、その必要条件は、

$$ \begin{aligned} & 1 + \mathbf{w}^{T} \mathbf{u}\frac{dh}{d\alpha}(\alpha + b) \geq 0 \\ \iff & \mathbf{w}^{T} \mathbf{u} \geq - \frac{1}{\frac{dh}{d\alpha}(\alpha + b)} \end{aligned} $$

となります。双曲線正接(tanh)の微分は$(\tanh x)’ = (\cosh x)^{-2}$で、この値の範囲は0から1ですので、$\mathbf{w}^{T} \mathbf{u} \geq -1$ならば十分であることが分かります。

この条件を満たすために、ニューラルネットの訓練中の$\mathbf{w}$, $\mathbf{u}$の更新の仕方を工夫します。通常通り、誤差逆伝搬で$\mathbf{w}$と$\mathbf{u}$を更新した後で、$\mathbf{u}$を次のように更新し直します。

$$ \hat{\mathbf{u}} = \mathbf{u} + [ m(\mathbf{w}^{T} \mathbf{u}) - \mathbf{w}^{T} \mathbf{u}] \frac{\mathbf{w}}{\| \mathbf{w} \|^2} $$

この$\hat{\mathbf{u}}$に$\mathbf{w}^{T}$を乗ずると、その値は$m(\mathbf{w}^{T} \mathbf{u})$となるので、関数$m(\cdot)$が$-1$より大きい値を取る関数、例えば$m(x) = -1 + \log(1 + e^x)$、のようにすることで、$\mathbf{w}^{T} \mathbf{u} \geq -1$が満たされます。

このように非線形関数$h$とパラメータ更新の仕方を工夫することで、関数の可逆性が保証されます。

実装例

PyTorchによる実装例を以下に示しておきます。全体の実装を確認したい方は、私のGitHub上にあるコードをご確認ください。

https://github.com/tatsy/normalizing-flows-pytorch

class PlanarTransform(nn.Module):
    def __init__(self, dim):
        super(PlanarTransform, self).__init__()

        self.dim = dim
        u = torch.randn(1, self.dim) * 0.01
        w = torch.randn(1, self.dim) * 0.01
        b = torch.randn(1) * 0.01

        self.register_parameter('u', nn.Parameter(u))
        self.register_parameter('w', nn.Parameter(w))
        self.register_parameter('b', nn.Parameter(b))
        self._make_invertible()

    def _make_invertible(self):
        u = self.u
        w = self.w
        w_dot_u = torch.mm(u, w.t())
        if w_dot_u.item() >= -1.0:
            return

        norm_w = w / torch.norm(w, p=2, dim=1)**2
        bias = -1.0 + F.softplus(w_dot_u)
        u = u + (bias - w_dot_u) * norm_w
        self.u.data = u.data

    def forward(self, z, log_df_dz):
        self._make_invertible()

        w_dot_u = torch.mm(self.u, self.w.t())
        affine = torch.mm(z, self.w.t()) + self.b

        z = z + self.u * torch.tanh(affine)
        det = 1.0 + w_dot_u * deriv_tanh(affine)
        log_df_dz = log_df_dz + torch.sum(torch.log(torch.abs(det) + 1.0e-5), dim=1)

        return z, log_df_dz

    def backward(self, z, log_df_dz):
        w_dot_z = torch.mm(z, self.w.t())
        w_dot_u = torch.mm(self.u, self.w.t())

        lo = torch.full_like(w_dot_z, -1.0e3)
        hi = torch.full_like(w_dot_z, 1.0e3)

        for _ in range(100):
            mid = (lo + hi) * 0.5
            val = mid + w_dot_u * torch.tanh(mid + self.b)
            lo = torch.where(val < w_dot_z, mid, lo)
            hi = torch.where(val > w_dot_z, mid, hi)

            if torch.all(torch.abs(hi - lo) < 1.0e-5):
                break

        affine = (lo + hi) * 0.5 + self.b
        z = z - self.u * torch.tanh(affine)
        det = 1.0 + w_dot_u * deriv_tanh(affine)
        log_df_dz = log_df_dz - torch.sum(torch.log(torch.abs(det) + 1.0e-5), dim=1)

        return z, log_df_dz

実験結果

この実験では、3つの正規分布を三角形状に並べた確率密度をNormalizing Flowにより正規分布に変換しています。以下の結果では正規分布から得たサンプルとNormalizing Flowの逆変換により目的分布を再現したものを比較しています。

なお、この学習では変分推論ではなく、

$$ \max \log p_Y(\mathbf{y}) = \max \left( \log p_Z(\mathbf{z}) + \log \left| \frac{\partial \mathbf{f}}{\partial \mathbf{y}} \right| \right) $$

という最尤推定により確率密度の変換を学習しています。

目的の分布	再現された分布

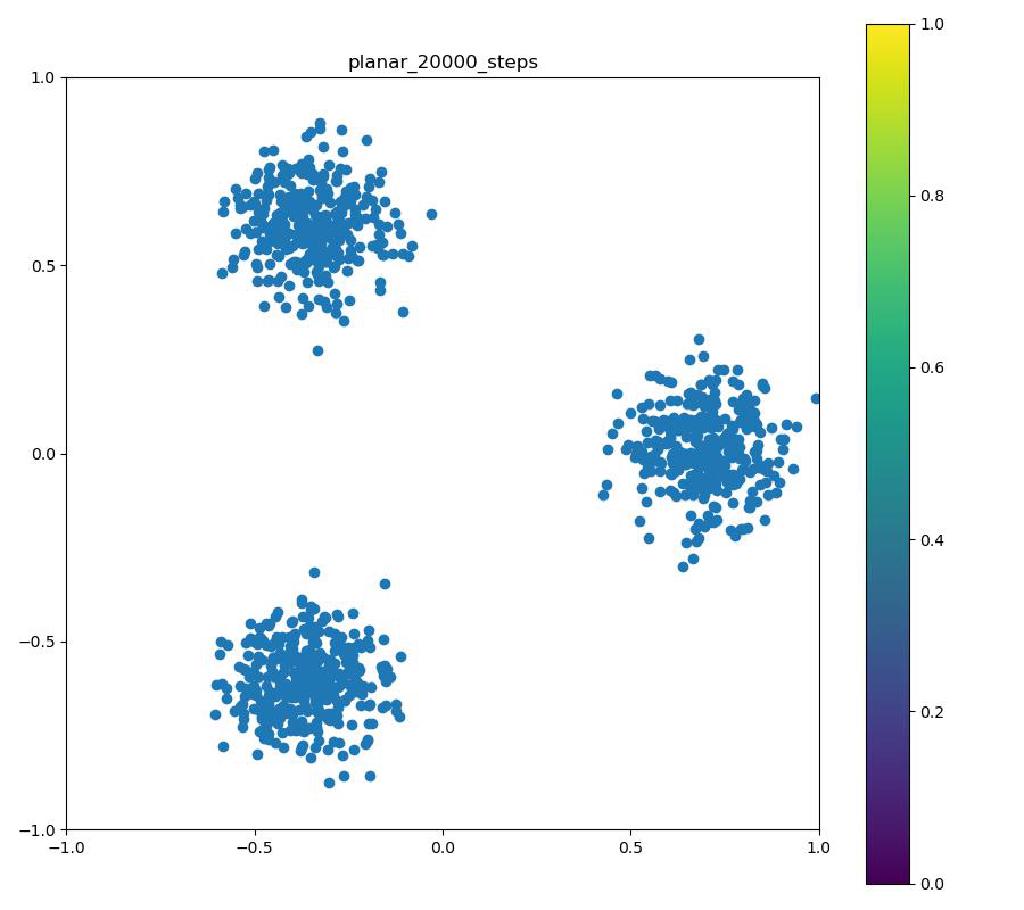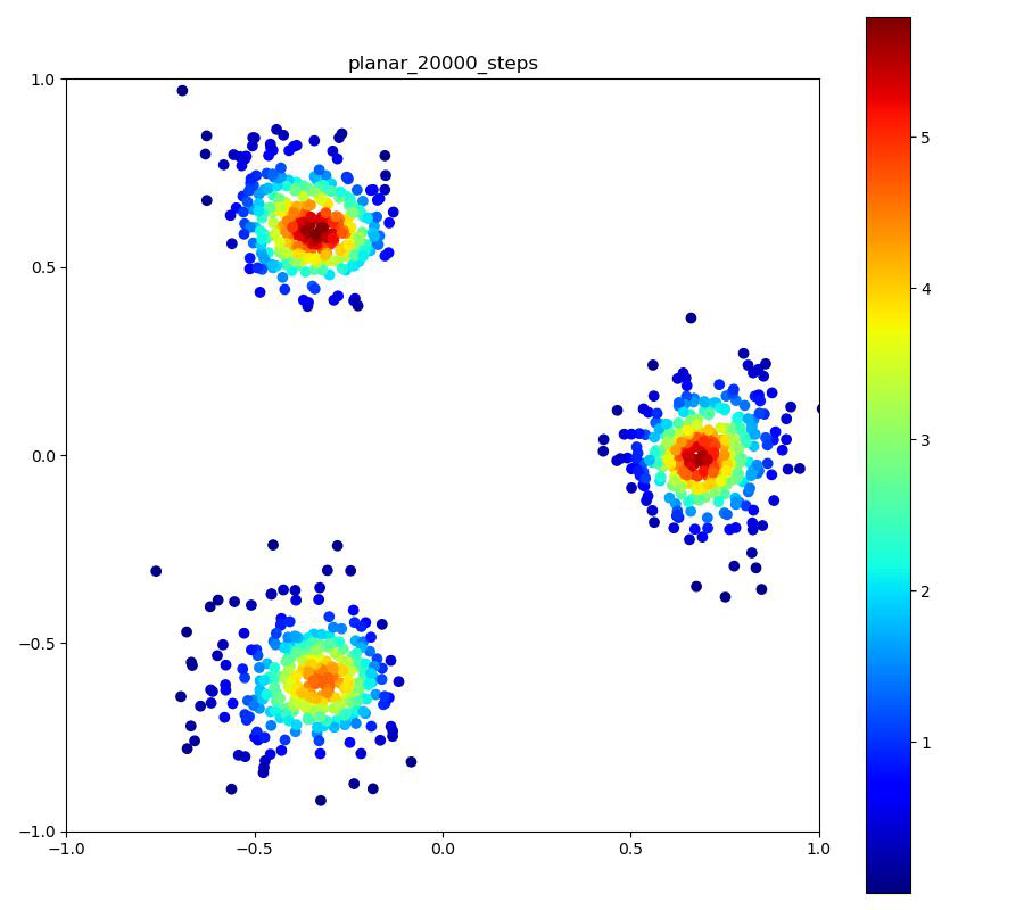※ 「目的の分布」についているカラーバーには意味はありません

まとめ

今回はNormalizing Flowが満たすべき条件と、最初期のNormalizing FlowであるPlanar Flowについて紹介しました。

Planar Flowでは、ヤコビアンの計算を簡単にするために、変数変換が内積と要素和、要素ごとの非線形関数の適用で構成されていました。しかしながら、Planar Flowはその定義式から$\mathbf{w}^{T} \mathbf{y} + b = 0$で定義される超平面に垂直な方向に分布を非線形に伸縮する効果と考えられるため、レイヤー数がかなり多くならないと、複雑な分布を表すことは難しいです。

また、Planar Flowは非線形の活性化関数がtanhですので、レイヤー数が多くなると、勾配消失が起こる可能性があり、実際にレイヤーの数を増やしてみても、それほど表現力は上がらず、上記の実験で正規分布を4つ以上に増やしてしまうと、学習がうまくいきませんでした。

また、逆関数の計算を可能とするために、非線形関数とパラメータの選び方を工夫しており、表現力がそれほど高くない割には、実装も複雑な印象が残ります。

次回以降では、より強力な変数変換を実現するための有力なアイディアの一つであるBijective Couplingについてご紹介いたします。

参考文献

[1] Redende et al., “Variational Inference with Normalizing Flows”, ICLR 2015. [arXiv]
[2] Dinh et al., “NICE: Non-linear independent components estimation”, arXiv 2014. [arXiv]