Normalizing Flow入門 第3回 Bijective Coupling

こんにちはtatsyです。Normalizing Flow入門の第3回です。

今回はNormalizing Flowの代表格であるReal NVP[1]などで使われており、その表現力を上げる上で重要なアイディアの一つであるBijective Couplingについてご紹介したいと思います。

ニューラルネットのヤコビアン

前回の記事では、Planar Flowを例にとって、最尤推定によって正規分布を目的の確率分布に変換する処理を学習させました。この処理では、確率$p_Y(\mathbf{y})$の尤度を最大化する問題を以下のように定義したのでした。

$$ \max \log p_Y(\mathbf{y}) = \max \left( \log p_Z(\mathbf{z}) + \log \left| \frac{\partial \mathbf{f}}{\partial \mathbf{y}} \right| \right) $$

この式を評価するためには、変数変換の関数$\mathbf{f}: \mathbb{R}^D \rightarrow \mathbb{R}^D$のヤコビアンに対して対数をとったものを評価する必要があるのですが、Planar Flowの場合にはこの計算が$\mathcal{O}(D)$の計算量で実現できました。

ですが、一般のニューラルネットに対してもヤコビアン自体は計算可能で、これを評価しても同じような処理が実現できそうです。例えば、PyTorchには、ニューラルネットにより定義された演算の勾配を計算する関数 torch.autograd.grad (リンク)が用意されており、これを用いることでヤコビアンを計算することが可能です。¹

この勾配計算の関数はスカラーを出力とする関数にしか使うことができないのですが、仮にベクトルを返すような関数でも、ベクトルの要素を1つずつ処理していくことでヤコビアンを計算できます。例えば、次のような感じです。

# 変数の定義
AA = torch.randn(5, 5)
bb = torch.randn(1, 5)
xx = torch.tensor(torch.randn(1, 5), requires_grad=True)

# 出力: yyは(1, 5)のサイズを持つ
yy = torch.mm(xx, AA.t()) + bb

## 各要素ごとの勾配
grads = []
for i in range(yy.size(1)):
    g = torch.autograd.grad(yy[:, i], xx, create_graph=True)[0]
    grads.append(g)

## ヤコビアン (AAと同じになる)
jacobian = torch.cat(grads, dim=0)

この処理自体には、問題はないのですが、このgrad関数はネットワークのグラフを遡りつつ自動微分することによって出力を得ているので、呼び出すごとにネットワークで定義される関数の評価と同等の計算量が必要です。

上記の計算では、出力ベクトルの各要素ごとにgradの計算をしているので、出力ベクトルの次元が大きくなると、急速に計算量が大きくなることは想像に難くないと思います。

従って、上記のようなナイーブなやり方ではダメで、ネットワークの作り方自体を工夫する必要があります。実際、その一例がPlanar Flowであったわけなのですが、残念ながらその表現力はそれほど高くありませんでした。²

Bijective Coupling

Bijective Couplingは変数変換のやり方を工夫することでヤコビアンの計算を簡単にする技術の一つです。

Bijective Couplingでは、入力のベクトルを2つのグループに次元方向で分割し、そのそれぞれの別々の処理を施します。ここでは、Dinhらが最初にBijective Couplingの考え方を紹介したNICE[2]に従って、その方法を紹介します。

今、入力のベクトル$\mathbf{y}$が$2D$次元のベクトルであるとして、前半$D$次元を$\mathbf{y}_1 \in \mathbb{R}^D$, 後半$D$次元を$\mathbf{y}_2 \in \mathbb{R}^D$とおきます。またCouplingレイヤーによって変換された後のベクトル$\mathbf{z}$についても同様に、前半を$\mathbf{z}_1$, 後半を$\mathbf{z}_2$とします。

ここで、$\mathbf{y}_2$を変数変換するためのパラメータを他方の$\mathbf{y}_1$のみから求める、というのがBijective Couplingの考え方です。NICEの場合には、Additive Couplingといって、$\mathbf{y}_1$から$\mathbf{y}_2$をどれだけ平行移動するのかを表す関数$\mathbf{t}(\mathbf{y}_1)$をニューラルネットで表します。

これを用いて、出力のベクトルを以下のように表します。

$$ \begin{aligned} \mathbf{z}_1 &= \mathbf{y}_1 \\ \mathbf{z}_2 &= \mathbf{y}_2 + \mathbf{t}(\mathbf{y}_1) \end{aligned} $$

すると、このような変換に対するヤコビ行列 $\partial \mathbf{z} / \partial \mathbf{y}$ は部分行列により次のように表せるはずです。

$$ \begin{equation} \begin{pmatrix} \frac{\partial \mathbf{z}_1}{\partial \mathbf{y}_1} & \frac{\partial \mathbf{z}_1}{\partial \mathbf{y}_2} \\ \frac{\partial \mathbf{z}_2}{\partial \mathbf{y}_1} & \frac{\partial \mathbf{z}_2}{\partial \mathbf{y}_2} \end{pmatrix} \label{eq:jacobian} \end{equation} $$

ここで、各部分行列に注目すると、$\partial \mathbf{z}_1 / \partial \mathbf{y}_1$ならびに$\partial \mathbf{z}_2 / \partial \mathbf{y}_2$は単位行列であり、$\partial \mathbf{z}_1 / \partial \mathbf{y}_2$ついてはゼロ行列であることが分かります。

この際、ニューラルネットワークによって定義されている$\mathbf{t}$を含む$\partial \mathbf{z}_2 / \partial \mathbf{y}_1$については、特殊な形にはならないのですが、式\eqref{eq:jacobian}と上記の議論によれば、ヤコビアンが対角要素を1とする下三角行列になっていることが分かります。

従って、上記の変換のヤコビアン、すなわちヤコビ行列の行列式は1であり、計算するまでもありません。この際、$\mathbf{y}_2$の変化量を決定する関数$\mathbf{t}$はどんなに複雑になっても良い、というのがBijective Couplingの強力な性質の一つです。

また、上記の変換では$\mathbf{z}_1 = \mathbf{y}_1$なので、逆変換についても、以下のような非常に単純な形で定義できます。

$$ \begin{aligned} \mathbf{y}_1 &= \mathbf{z}_1 \\ \mathbf{y}_2 &= \mathbf{z}_2 - \mathbf{t}(\mathbf{z}_1) \end{aligned} $$

以上から、NICEのBijective Couplingが前回の記事で紹介したNormalizing Flowの持つべき性質である、

• 変換が可逆であること
• 関数とその逆関数ならびにヤコビアンが簡単に評価できること

という性質を満たしていることが分かります。さらに、$\mathbf{t}$がどんなに複雑になっても良い、という性質から一定以上の表現力が期待できます。

ここまでの説明では、$\mathbf{y}_1$から求まる変形量を用いて$\mathbf{y}_2$を変形していましたが、この関係を入れ替えて、$\mathbf{y}_2$から求まる変形量により$\mathbf{y}_1$を変形するという操作を交互に行うことでベクトル$\mathbf{y}$全体が徐々に変換されていきます。

Couplingを用いたNormalizing Flow

それでは次にBijective Couplingを用いた手法の例として、Real NVP[1]とFlow++[3]について見ていきます。

Real NVP

Real NVPは、変数変換にあたり、NICEで平行移動成分のみしか計算していなかったものに、スケーリングの成分を追加して拡張したものです。Real NVPの変数変換は次の形で定義されます。

$$ \begin{aligned} \mathbf{z}_1 &= \mathbf{y}_1 \\ \mathbf{z}_2 &= \exp(\mathbf{s}(\mathbf{y}_1)) \odot \mathbf{y}_2 + \mathbf{t}(\mathbf{y}_1) \end{aligned} $$

この式で$\odot$はベクトルの要素ごとの積を表すものとします。すると、この変換のヤコビ行列は、次のような形を持つことが分かります。

$$ \begin{equation} \begin{pmatrix} \mathbf{I}_D & \mathbf{0} \\ \frac{\partial \mathbf{z}_2}{\partial \mathbf{y}_1} & \mathrm{diag}(\exp \left( \mathbf{s}(\mathbf{y}_1) \right)) \end{pmatrix} \label{eq:realnvp-jacobian} \end{equation} $$

ただし、$\mathbf{I}_D \in \mathbb{R}^{D \times D}$は単位行列、$\mathrm{diag}(\mathbf{s})$はベクトル$\mathbf{s}$を対角要素にもつ対角行列であるとします。

すると、Real NVPのヤコビ行列もNICEの時と同様に、下三角行列になっていることが分かります。今回の対角要素はベクトル$\exp(\mathbf{s})$の各要素になっているので、ヤコビアンはこれらの要素の積となり、こちらも少ない計算量($\mathcal{O}(D)$)で計算可能です。

また、Real NVPの論文では、変数変換を定義する関数$\mathbf{s}$, $\mathbf{t}$にresidual networkを適応していたり、ネットワークの中にバッチ正規化を入れていたりと、変換自体にも大きな進歩が見られます。

加えて、確率密度の推定だけではなく、画像生成のようなタスクにも有効なチェッカーボードパターンを用いたベクトル(テンソル)の分割や、多重解像度でNormalizing Flowを適用するmultiscale architectureについても紹介しているなど、内容が盛り沢山です。興味がある方はぜひ元論文を読んでいただきたいです (リンク)。

Flow++

Bijective Couplingを使う手法の中では比較的新しいFlow++は、Couplingの関数を線形のアフィン変換ではなく、非線形の演算へと拡張したものです。Flow++では、次のように変数変換を行います。

$$ \begin{aligned} \mathbf{z}_1 &= \mathbf{y}_1 \\ \mathbf{z}_2 &= \sigma^{-1} \left[ \sum_{k=1}^{K} \pi_k(\mathbf{y}_1) \sigma \left[ (\mathbf{y}_2 - \boldsymbol\mu_k(\mathbf{y}_1)) \exp(\mathbf{s}_k(\mathbf{y}_1)) \right] \right] \exp(\mathbf{a}(\mathbf{y}_1)) + \mathbf{b}(\mathbf{y}_1) \end{aligned} $$

この式で$\sigma[\cdot]$はシグモイド関数、$\sigma^{-1}$はロジット関数(シグモイド間数の逆関数)を表します。Flow++では、変数変換のパラメータとして$\pi_k$, $\boldsymbol\mu_k$, $\mathbf{s}_k$, $\mathbf{a}$, $\mathbf{b}$をニューラルネットを用いて推定します。

変換式だけを見ると、かなり複雑で、実際にヤコビアンを計算できるのかが、やや不安になりますが、$\partial \mathbf{z}_2 / \partial \mathbf{y}_2$はシグモイド関数とロジット関数の微分を用いて確かに計算可能で、この結果がヤコビ行列の対角成分に現れます。

いずれの計算もベクトルの要素ごとの計算ですので、$K$個のシグモイドの和を取る処理が入りますので、計算量は$\mathcal{O}(DK)$となります。$K$は変数変換するベクトルの次元に比べれば小さく抑えられると考えられますので、計算量もそれほど大きくはなりません。

次に逆関数の計算ですが、この変換は残念ながら解析的には逆関数を書き表すことができません。ですが、上記の表現でロジット関数の中に入っているシグモイド混合分布の部分は$\mathbf{y}_2$に対して単調増加する関数になっているので、両辺のシグモイドを取ることで、二分法により$\mathbf{z}_2$から$\mathbf{y}_2$を求めることが可能です。

Flow++の論文では、上記のシグモイド混合分布を用いたCouplingの他にも、パラメータ推定への自己注意(self attention)機構の導入や、離散的な分布に対してNormalizing Flowを適用するための非量子化 (dequantization)について議論しています。こちらも、興味のある方はぜひ元論文を読んでみてください (リンク)。

実装例 (Real NVP)

参考に、Real NVPで用いているAffine Couplingの実装例を示しておきます。Flow++の実装例についても、私のGitHubで公開していますので、ご興味のある方は、こちらを参照ください。

https://github.com/tatsy/normalizing-flows-pytorch

class AffineCoupling(AbstractCoupling):
    """
    affine coupling used in Real NVP
    """
    def __init__(self, dims, odd=False):
        super(AffineCoupling, self).__init__(dims, odd)
        if len(dims) == 1:
            in_chs = dims[0] // 2 if not odd else (dims[0] + 1) // 2
            out_chs = dims[0] - in_chs
            self.net_s = MLP(in_chs, out_chs)
            self.net_t = MLP(in_chs, out_chs)
        elif len(dims) == 3:
            self.net_s = ConvNet(dims[0] * 2, dims[0] * 2)
            self.net_t = ConvNet(dims[0] * 2, dims[0] * 2)

    def _transform(self, z0, z1, log_df_dz):
        t = self.net_t(z1)
        s = torch.tanh(self.net_s(z1))
        z0 = z0 * torch.exp(s) + t
        log_df_dz += torch.sum(s.view(z0.size(0), -1), dim=1)

        return z0, z1, log_df_dz

    def _inverse_transform(self, y0, y1, log_df_dz):
        t = self.net_t(y1)
        s = torch.tanh(self.net_s(y1))
        y0 = torch.exp(-s) * (y0 - t)
        log_df_dz -= torch.sum(s.view(y0.size(0), -1), dim=1)

        return y0, y1, log_df_dz

実験結果

Real NVP

目的の分布	再現された分布	GIF (画像をクリック)

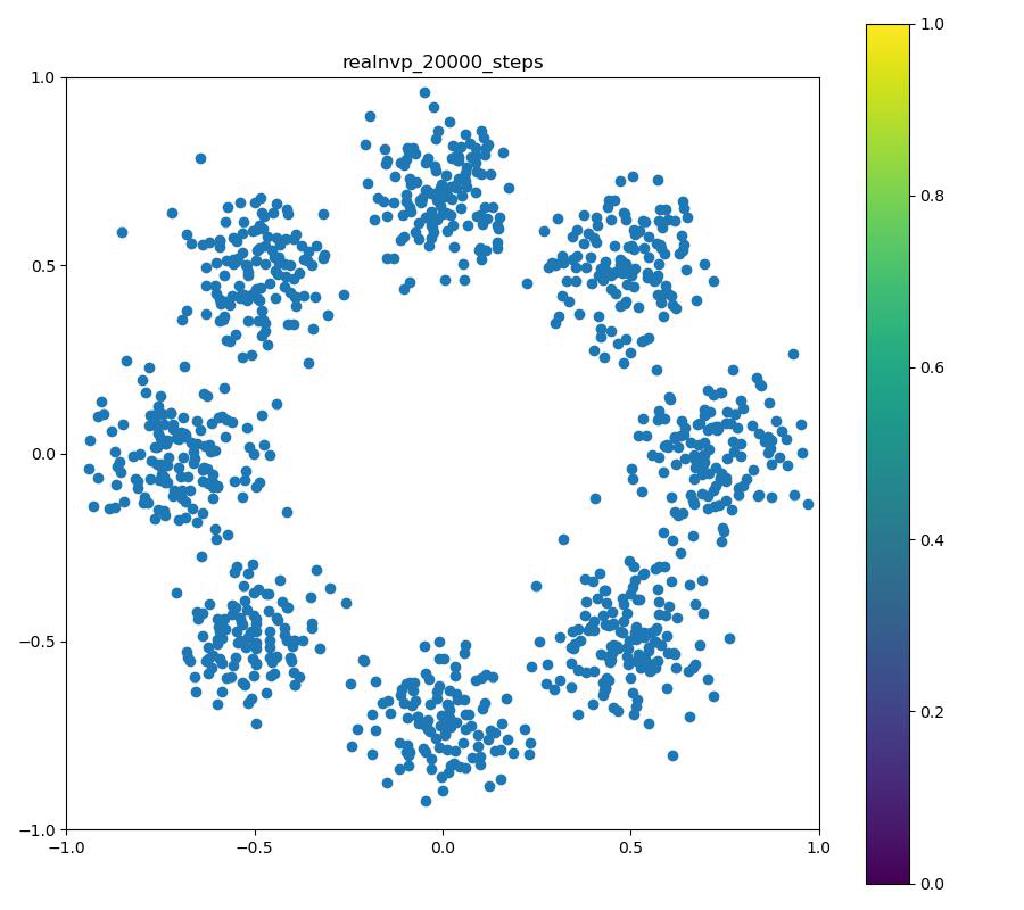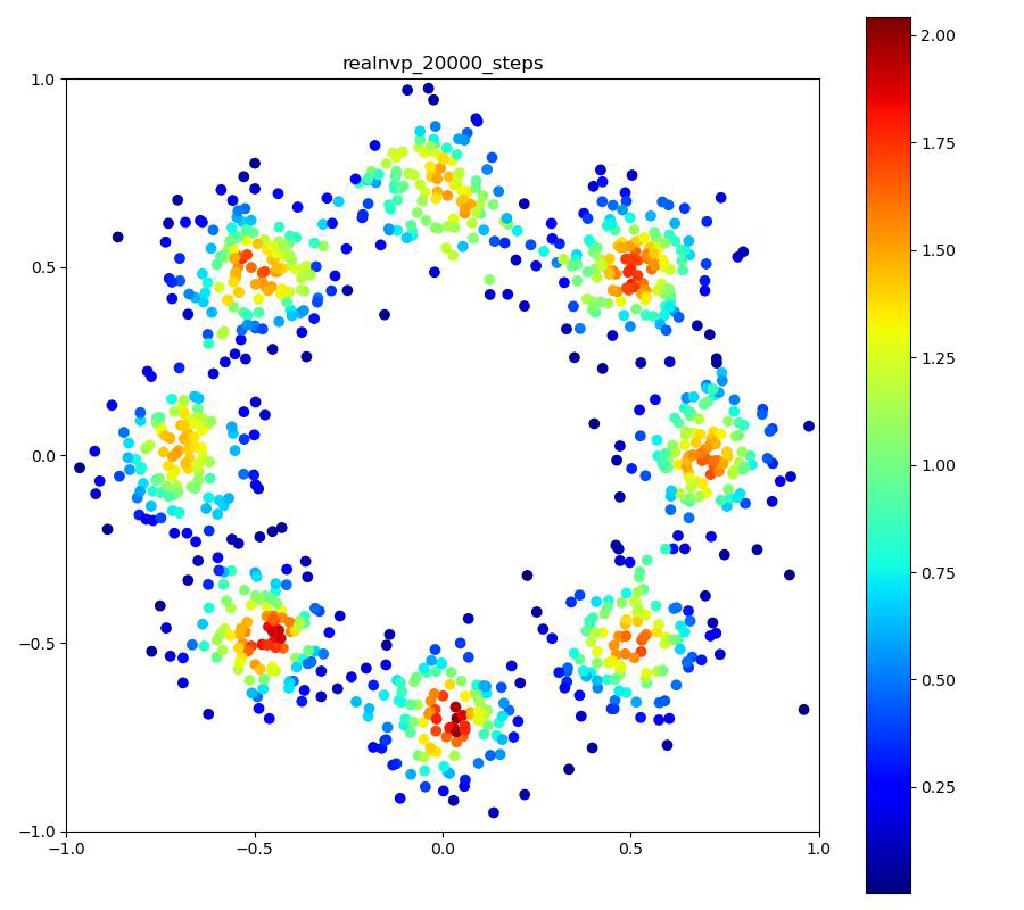Flow++

目的の分布	再現された分布	GIF (画像をクリック)

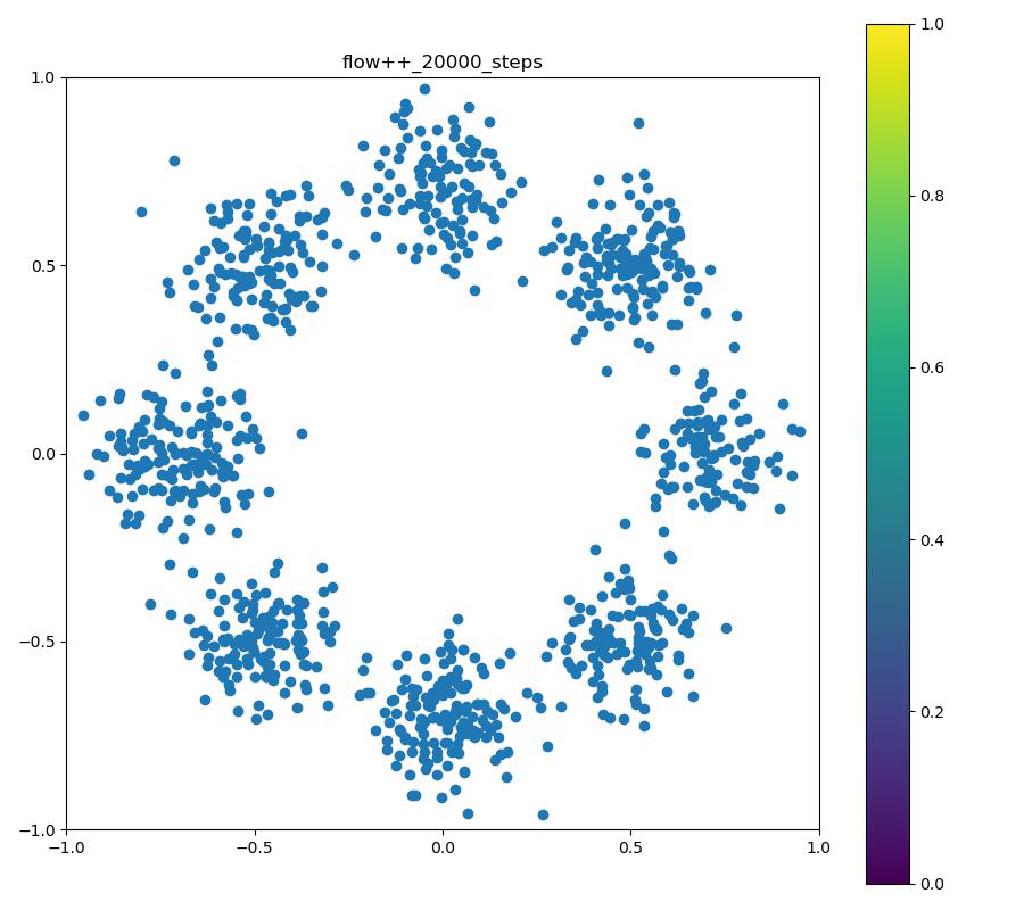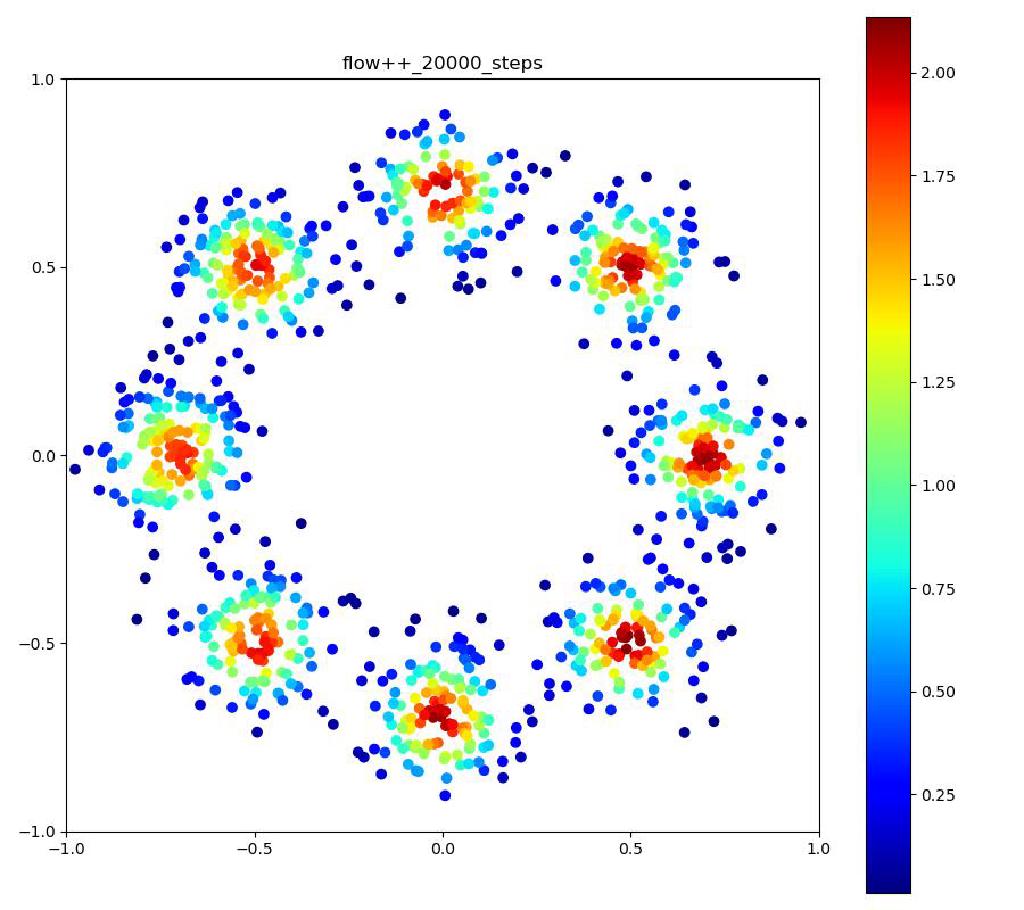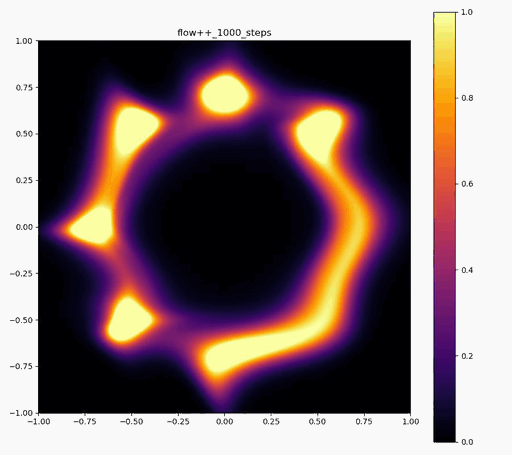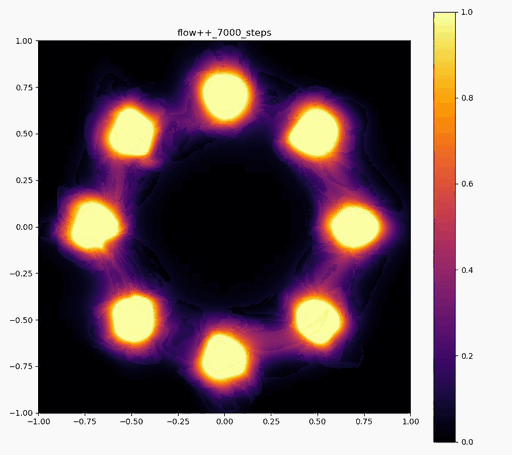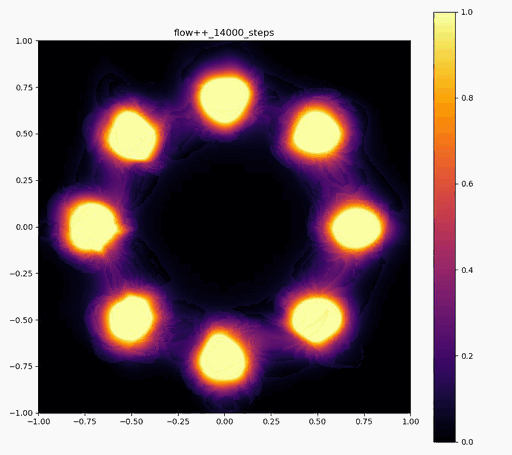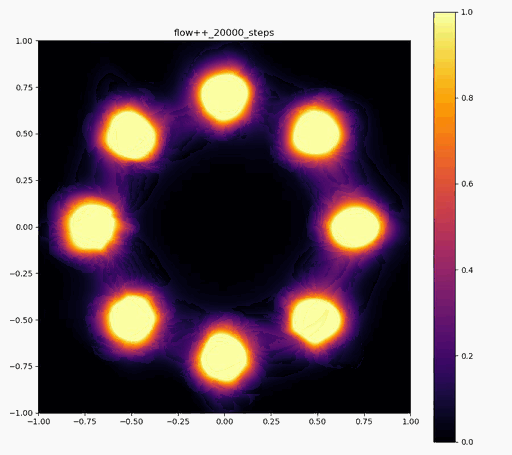余談

Flow++では、シグモイド混合分布の重み付き和の対数を取る必要があるのですが、シグモイド関数の対数を取る

$$ \log \left( \frac{1}{1 + e^{-x}} \right) = -\log (1 + e^{-x}) $$

という計算は$x$が負の大きな値の時は、およそ$x$になるはずですが、$\exp$の計算は$-x$に対して値が急速に大きくなるため、このまま計算してしまうと値がアンダーフローしてしまい、$x$が$-100$程度になると、マイナス無限大を出力するようになってしまいます。

これをそのまま計算する代わりにソフトプラス関数 ($\log(1 + e^x)$)に$-x$を入力する(logsigmoidという関数もある)と、より正しく計算できるようになるので、シグモイド混合分布の計算においても、そのまま式を評価していって、最後に対数を取るよりも、最初から対数で計算を進めて行った方が数値安定性が高くなります。

x = torch.tensor([-100.])
print(torch.log(torch.sigmoid(x)))  # tensor([-inf])
print(-F.softplus(-x)) # tensor([-100.])
print(F.logsigmoid(x)) # tensor([-100.])

また、幸運なことに、PyTorchやTensorFlowにはlogsumexpという関数が用意されていて、これはある数列${ a_1, \ldots, a_N }$が与えられた時に、

$$ \mathrm{logsumexp}({ a_i }) = \log \left( \sum_i \exp a_i \right) $$

という計算を行ってくれます。従って、上記の議論に従って、$\log \sigma(x_i)$と$\log \pi_i$を計算しておき、$a_i = \log \pi + \log \sigma(x_i)$としてlogsumexpを用いれば、上記のシグモイド混合分布の対数をより安定的に計算できるようになります。

実際に、これを使う場合と、使わない場合とでは、終盤の精度の向上に大きな差が現れるので、自分で実装される方は、このあたりをご留意いただくと良いのかなと思います。

まとめ

今回の記事ではNormalizing Flowを実現する強力な技術であるBijective Couplingと、それを用いた代表的な手法である、NICE, Real NVP, Flow++について紹介しました。

Bijective Couplingは、これ以外のNormalizing Flowの手法と比べて実装が簡単で、その割に表現力が非常に高いためCGの分野でも、レンダリングのための重要度サンプリングなどに利用されています[4]。

ですが、実際に実験してみると、確率変数のサンプルは確かにうまくいくのですが、それらのサンプルに対する確率密度の計算に結構ブレがあり、実際に目指したい分布と比べた時に、極端に密度が大きかったり小さかったりする場所が現れてしまいます (上記の実験結果で正規分布周辺に現れる尻尾のような部分)。

次回以降は、このBijective Couplingの問題を補助的に解決したり、全く別のアプローチからより良いNormalizing Flowを目指す技術について紹介していきます。

参考文献

[1] Dinh et al., “Real NVP for density estimation,” ICLR 2017. [arXiv]
[2] Dinh et al., “NICE: Non-linear independent components estimation,” arXiv 2014. [arXiv]
[3] Ho et al., “Flow++: Improving Flow-Based Generative Models with Variational Dequantization and Architecture Design,” ICML 2019. [arXiv]
[4] Zheng et al., “Learning to Importance Sample in Primary Sample Space,” Computer Graphics Forum, 2019.