Normalizing Flow入門第4回 Glow

Tatsuya Yatagawa

2021-01-07

こんにちはtatsyです。Normalizing Flow入門の第4回です。

今回は前回紹介したBijective Couplingに基づく手法でありながらも、いくつかの工夫により表現力を向上させたGlow[1]についてご紹介したいと思います。

Glow

今回紹介するGlowはReal NVPをベースにしており、スケーリングと平行移動を組み合わせた変数変換 (Affine Coupling)に加えてActnormとInvertible 1x1 Convolutionという処理を付け加えることで、表現力の向上を測っています。

Actnorm

Actnormはバッチ正規化のように入力されてきたデータの平均位置とスケールをアフィン変換により変更するレイヤーです。Real NVPでは正規化のためにバッチ正規化が使われていましたが、バッチ正規化はミニバッチのサイズが小さくなると性能が低下することが知られている(といっても経験上はそれなりにうまく動く)。

一方で、Glowで提案されるActnormでは、スケールと平行移動のパラメータは一番最初に入ってきたデータの平均と標準偏差を用いて初期化され、その後は訓練データに依存しない形で誤差逆伝搬により更新されていきます。これにより、仮に訓練に使うミニバッチのサイズが小さい場合でも、学習の中で良い正規化のパラメータを見つけて行こう、というのがActnormの考え方です。

ただ、今だと、正規化のやり方もバッチ正規化以外にグループ正規化などもあって、必ずしもバッチサイズが小さいとうまくいかないものばかりではないので、Normalizing Flowの分野ではよく使われてはいるものの、Actnormが常に良いというわけでもないとは思います。

Invertible 1x1 Convolution

画像に対して畳み込み計算をする時に、カーネルサイズが1×1である場合には、その計算は、画素ごとに特徴ベクトルをアフィン変換する操作(スケーリングして、バイアスベクトルを足す)であると考えることができます。特に、畳み込み層の入出力のチャネル数が同じである場合には、この操作は(バイアスベクトルを考えなければ)正方行列$\mathbf{A}$を掛け算する操作に対応します。しかも、畳み込み層の場合には掛け算される正方行列$\mathbf{A}$は全ての画素で共通です。

ということは、画像の持っている特徴ベクトルを全てフラットなベクトルと考えて、1x1の畳み込み操作を行列として表すと、各画素に掛け算される正方行列$\mathbf{A}$をブロック対角成分に持つような疎行列が、この操作の正体であることが分かります。

ブロック対角行列の行列式は、各ブロック行列の行列式の積に等しいので、実際には$\mathbf{A}$の行列式を求めて、それを画素数分だけ掛け算すればよく、最尤推定に用いる場合には、対数を取った後に画素数分だけたしあげれば十分です。

ただ、それでも、ヤコビ行列の計算の度に行列式を求めるのは効率的ではないので、Glowでは、最初に行列$\mathbf{A}$をLU分解して$\mathbf{A} = \mathbf{LU}$と表しておきます。

一般に、ガウスの消去法などでLU分解を行う時には、計算精度を高めるためにピボット選択をして、そのピボットの値で各列(あるいは行)の値を割り算するので、$\mathbf{L}$か$\mathbf{U}$のいずれかは対角要素が全て1の行列になっています。行列の積の行列式は、各行列の行列式の積に等しいので、ヤコビアンを求める際には$\mathbf{L}$か、$\mathbf{U}$のどちらかの対角要素の積だけを求めれば良いことになります。

従って、1x1の畳み込みカーネルによる畳み込み演算は用意にヤコビアンが計算可能で、LU分解を用いていることから、その逆演算も各画素が持つ特徴ベクトルの次元を$D$として$\mathcal{O}(D^2)$の範囲には収まっています。

このように、1x1の畳み込み演算はNormalizing Flowの満たすべき条件を満たすことが分かりましたが、果たして、この演算にはどのような意味があるのでしょうか？ 前回紹介したReal NVPでは、入力ベクトル$\mathbf{y}$の前半部分$\mathbf{y}_1$と後半部分$\mathbf{y}_2$を交互に入れ替えながら変形を行っていました。

Glowの1x1畳み込みは、この入れ替えの操作を一般化したものと考えることができて、Real NVPでそのままチャンネルの順序を入れ替えていたものを、アフィン変換により変形して基底の変化を行っていると考えることができます。この一般化により、Real NVP以上の性能が期待できるというわけです。

実装例

Actnorm

class ActNorm(nn.Module):
    def __init__(self, num_features, eps=1.0e-5):
        super(ActNorm, self).__init__()
        self.num_features = num_features
        self.eps = eps

        self.dimensions = [1] + [1 for _ in num_features]
        self.dimensions[1] = num_features[0]
        self.log_scale = nn.Parameter(torch.zeros(self.dimensions), requires_grad=True)
        self.bias = nn.Parameter(torch.zeros(self.dimensions), requires_grad=True)
        self.initialized = False

    def forward(self, z, log_df_dz):
        if not self.initialized:
            z_reshape = z.view(z.size(0), self.num_features[0], -1)
            log_std = torch.log(torch.std(z_reshape, dim=[0, 2]) + self.eps)
            mean = torch.mean(z_reshape, dim=[0, 2])
            self.log_scale.data.copy_(log_std.view(self.dimensions))
            self.bias.data.copy_(mean.view(self.dimensions))
            self.initialized = True

        z = (z - self.bias) / torch.exp(self.log_scale)

        num_pixels = np.prod(z.size()) // (z.size(0) * z.size(1))
        log_df_dz -= torch.sum(self.log_scale) * num_pixels
        return z, log_df_dz

    def backward(self, y, log_df_dz):
        y = y * torch.exp(self.log_scale) + self.bias
        num_pixels = np.prod(y.size()) // (y.size(0) * y.size(1))
        log_df_dz += torch.sum(self.log_scale) * num_pixels
        return y, log_df_dz

Invertible 1x1 Convolution

class InvertibleConv1x1(nn.Module):
    """
    invertible 1x1 convolution used in Glow
    """
    def __init__(self, in_out_channels):
        super(InvertibleConv1x1, self).__init__()

        W = torch.zeros((in_out_channels, in_out_channels), dtype=torch.float32)
        nn.init.orthogonal_(W)
        LU, pivots = torch.lu(W)

        P, L, U = torch.lu_unpack(LU, pivots)
        self.P = nn.Parameter(P, requires_grad=False)
        self.L = nn.Parameter(L, requires_grad=True)
        self.U = nn.Parameter(U, requires_grad=True)
        self.I = nn.Parameter(torch.eye(in_out_channels), requires_grad=False)
        self.pivots = nn.Parameter(pivots, requires_grad=False)

        L_mask = np.tril(np.ones((in_out_channels, in_out_channels), dtype='float32'), k=-1)
        U_mask = L_mask.T.copy()
        self.L_mask = nn.Parameter(torch.from_numpy(L_mask), requires_grad=False)
        self.U_mask = nn.Parameter(torch.from_numpy(U_mask), requires_grad=False)

        s = torch.diag(U)
        sign_s = torch.sign(s)
        log_s = torch.log(torch.abs(s))
        self.log_s = nn.Parameter(log_s, requires_grad=True)
        self.sign_s = nn.Parameter(sign_s, requires_grad=False)

    def forward(self, z, log_df_dz):
        L = self.L * self.L_mask + self.I
        U = self.U * self.U_mask + torch.diag(self.sign_s * torch.exp(self.log_s))
        W = self.P @ L @ U

        B = z.size(0)
        C = z.size(1)
        z = torch.matmul(W, z.view(B, C, -1)).view(z.size())

        num_pixels = np.prod(z.size()) // (z.size(0) * z.size(1))
        log_df_dz += torch.sum(self.log_s, dim=0) * num_pixels

        return z, log_df_dz

    def backward(self, y, log_df_dz):
        with torch.no_grad():
            LU = self.L * self.L_mask + self.U * self.U_mask + torch.diag(
                self.sign_s * torch.exp(self.log_s))

            y_reshape = y.view(y.size(0), y.size(1), -1)
            y_reshape = torch.lu_solve(y_reshape, LU.unsqueeze(0), self.pivots.unsqueeze(0))
            y = y_reshape.view(y.size())

        num_pixels = np.prod(y.size()) // (y.size(0) * y.size(1))
        log_df_dz -= torch.sum(self.log_s, dim=0) * num_pixels

        return y, log_df_dz

実験結果

以下の実験結果だけをみると、Real NVPに比べ、Glowの方が8つの正規分布周辺に現れる細い筋のような領域が若干減っているように見えます。

Glow

目的の分布	再現された分布	GIF (画像をクリック)

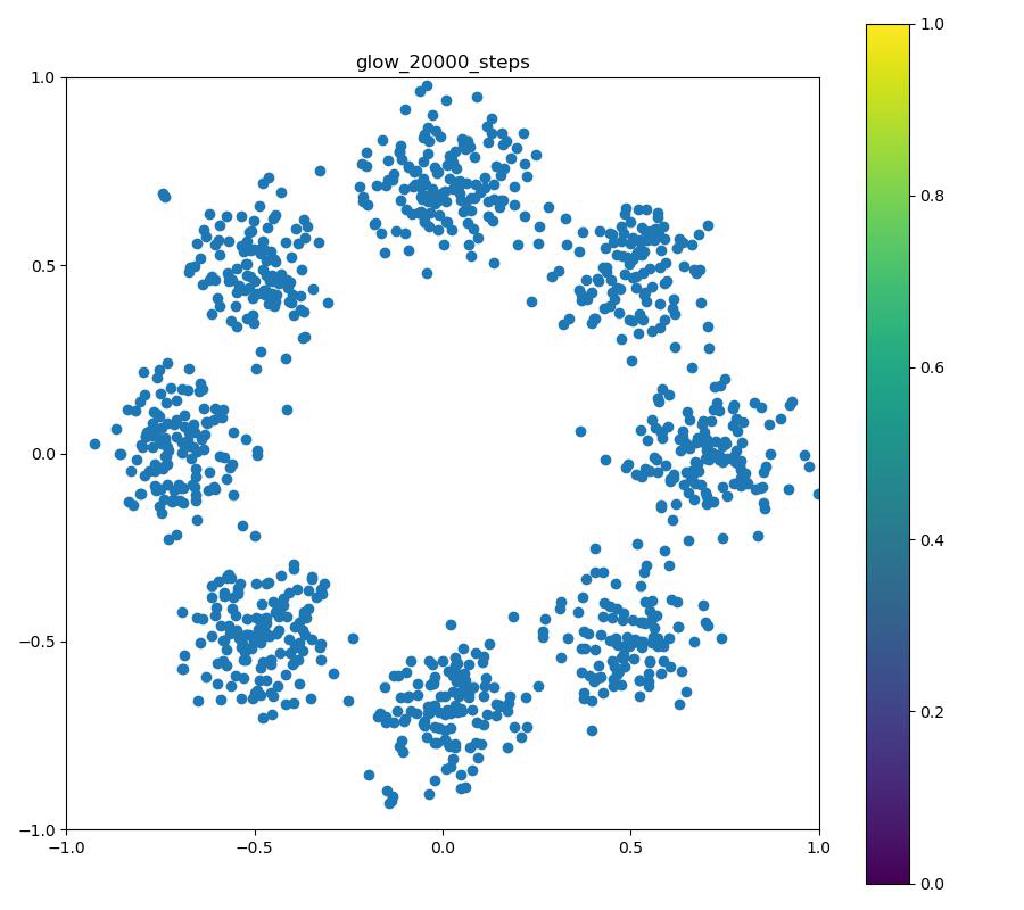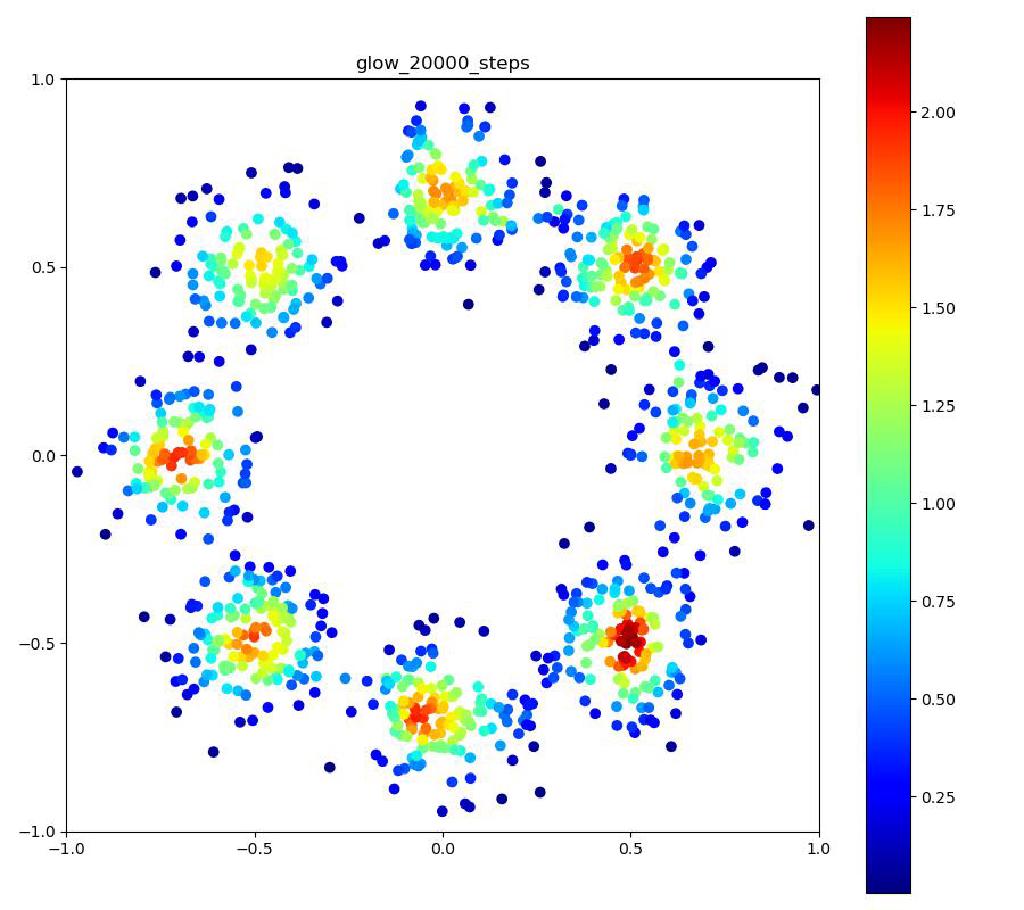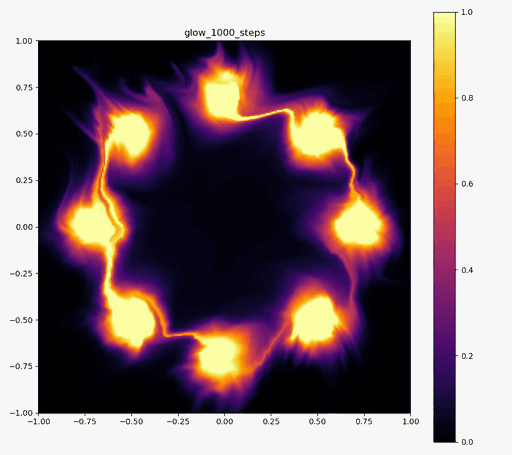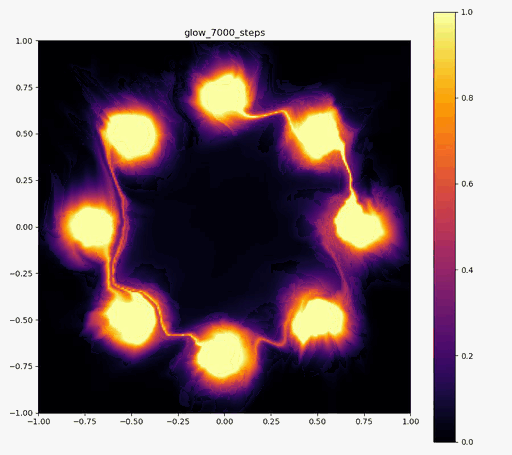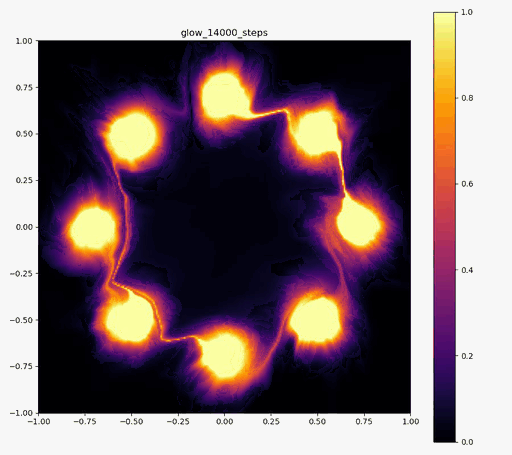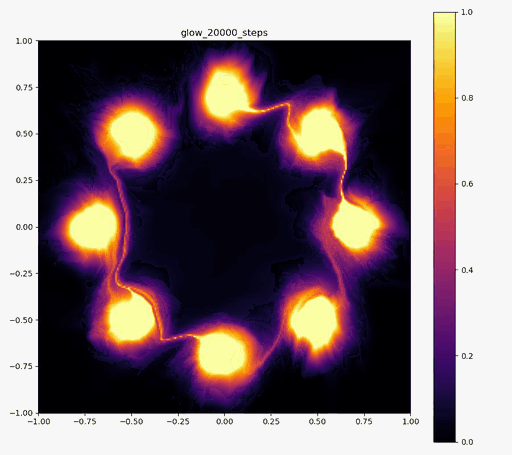Real NVP (比較用, 前回と同じ)

目的の分布	再現された分布	GIF (画像をクリック)

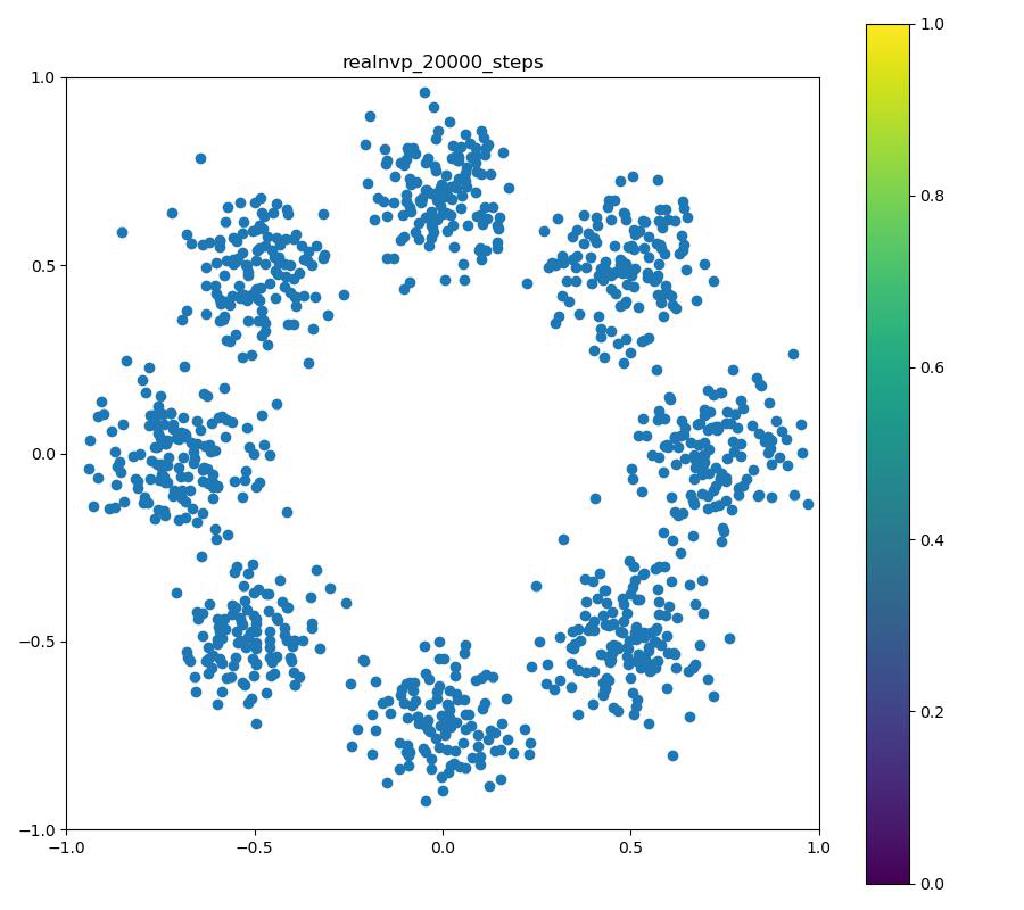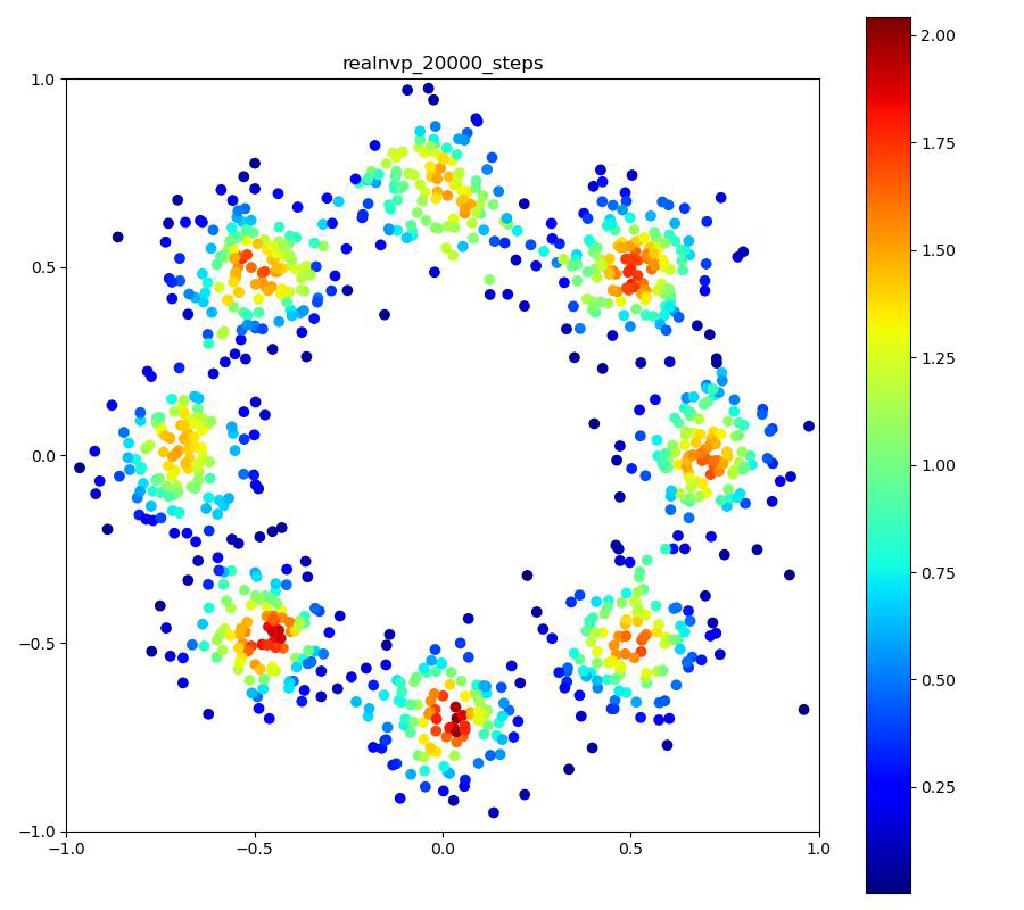まとめ

今回はBijective Couplingを用いた手法でありつつも、ActnormとInvetible 1x1 Convolutionという新しい工夫を取り入れたGlowについて紹介いたしました。

この論文で紹介された、これら二つの技術は、後続の論文でもそれなりに使われていて、比較対象にもなっているので、Normalizing Flowの分野では比較的著名な論文かと思います。

次回はBijective Couplingの考え方を少し変更したAutoregressive Flowについてご紹介したいと思います。

参考文献

[1] Kingma and Dhariwal, “Glow: Generative Flow with Invertible 1x1 Convolution,” arXiv 2018. [arXiv]