Normalizing Flow入門 第5回 Autoregressive Flow
こんにちはtatsyです。Normalizing Flow入門の第5回です。だんだん、入門なのかどうか分からなくなってきました。
今回は、Bijective Couplingの考え方を改良したAutoregressive Flowについてご紹介したいと思います。
今回の記事の中で紹介する2つの手法、Inverse Autoregressive Flow (IAF)[1]とMasked Autoregressive Flow (MAF)[2]は考え方はほとんど同じであるにも関わらず、その目的によってネットワークの構成の仕方が異なるという点がとても面白いところだと思います。
Autoregressive Flow
Autoregressiveという言葉は、日本語でいうと自己回帰という言葉に対応していて、とある時系列状のデータ
$$ x_1, x_2, \ldots, x_t, x_{t + 1}, \ldots $$
の中で、$x_t$がそれ以前の状態 $x_1, x_2, \ldots, x_{t-1}$のみに依存するようなモデルを指します。
Normalizing Flowでは、確率変数ベクトル$\mathbf{y}$を別の確率変数ベクトル$\mathbf{z}$に変換する際、$\mathbf{z}$の各次元$z_t$が、それ以前の$\mathbf{y}$の状態$y_t$にのみ依存することをAutoregressive Flowと呼んでいます。
つまり、新たな次元$y_t$を$z_t$に変換するとき、その変換パラメータ$\Theta$が$y_1, \ldots, y_{t-1}$だけに依存していて、その変換関数$h(y_t)$が、
$$ z_t = h(y_t; \Theta(\mathbf{y}_{1:t-1})) $$
のように表せると考えます。なお$\mathbf{y}_{1:t}$という表記は、Pythonのスライス表記に対応していて、ベクトル$\mathbf{y}$の1から$t$次元目までを取り出したベクトルを指すものとします。
すると、ある次元$z_t$の$\mathbf{y}$の各要素$y_1, \ldots, y_D$の微分というのは次のように書けます。
$$ \frac{\partial h(z_t)}{\partial y_d} = \frac{\partial h(z_t)}{\partial y_d} = \begin{cases} \displaystyle \frac{\partial h(y_t; \Theta(\mathbf{y}_{1:t-1}))}{\partial \Theta(\mathbf{y}_{1:t-1})} \cdot \frac{\partial \Theta(y_{1:t-1})}{\partial y_d} & (d < t) \\ h’(y_t; \Theta(\mathbf{y}_{1:t-1})) & (d = t)\\ 0 & (d > t) \end{cases} $$
従って$\mathbf{z}$全体と$\mathbf{y}$全体の関係で見ると、この変数変換のヤコビ行列はBijective Couplingの時と同様にした三角行列になることが分かります。
従って、Normalizing Flowで用いる際には、各次元を変換する関数$h$の微分を$D$次元分保持しておいて、その積を取ることでヤコビアンを計算することができるというわけです。
この構成方法を用いると、一見$\mathbf{z}$の各次元を順々に評価していく必要があるように見えるのですが、ニューラルネットの構成方法を工夫することで、一度に全次元を評価することができます。これはGermainらが提案したMADE[3]という手法で提案されていますので、最初にその構成方法を見てみます。
Masked Autoencoder for Density Estimation (MADE)
ニューラルネットの計算、特にベクトルを全結合層によって変換する計算というのは、パラメータ$\mathbf{W}$, $\mathbf{b}$並びに非線形の活性化関数$h$を用いて次のように表せます。
$$ \begin{equation} \hat{\mathbf{x}} = h(\mathbf{W} \mathbf{x} + \mathbf{b}) \label{eq:fully-connection} \end{equation} $$
この構成において、とある次元$d$だけに注目すると、上の式は次のように書き直せます。
$$ \hat{x}_d = h(\mathbf{w}_d^T \mathbf{x} + b_d) $$
この式にたいして、入力の$\mathbf{x}$の最初$t-1$次元だけを取り出すマスクを$\mathbf{m}_{1:t-1}$を適用すると、次のように書き直せます。
$$ \hat{x}_d = h(\mathbf{w}_d^T (\mathbf{m}_{1:d-1} \odot \mathbf{x}) + b_d) $$
すると、この式では$\hat{x}_d$は$d$よりも前の次元$\mathbf{x}_{1:d-1}$にしか依存していないことが分かります。これを各次元$d$に適用して、式\eqref{eq:fully-connection}を書き直すと、
$$ \begin{gather} \hat{\mathbf{x}} = h((\mathbf{W} \odot \mathbf{M}) \mathbf{x} + \mathbf{b}) \\ \mathbf{M} = \left(\mathbf{m}_{1:1} \cdots \mathbf{m}_{1:D} \right) \end{gather} $$
言い換えればマスク行列$\mathbf{M}$は対角成分を持たない狭義の下三角行列になっています。この書き方は一般的なニューラルネットに対して拡張可能なので、$h$の撮り方を例えばReLUなどに変更することも可能で、多層のニューラルネットも構成することができます。MADEの元論文では、単一の隠れ層を持つニューラルネットで出力の活性化関数がシグモイドであるようなものが以下のように書かれています。
$$ \begin{gather} \mathbf{h}(\mathbf{x}) = \mathbf{g}(\mathbf{b} + (\mathbf{W} \odot \mathbf{M}^{\mathbf{W}}) \mathbf{x}) \\ \hat{\mathbf{x}} = \mathrm{sigm}(\mathbf{c} + (\mathbf{V} \odot \mathbf{M}^{\mathbf{V}}) \mathbf{h}(\mathbf{x})) \end{gather} $$
表記については元のMADE論文中での表記に揃えてありますので、ご注意ください。このように隠れ層を入れる場合には、マスク$\mathbf{M}^{\mathbf{W}}$と$\mathbf{M}^{\mathbf{V}}$の作り方に少し自由度が出てきます。
この場合に満たすべき条件は$\mathbf{M}^{\mathbf{V}} \mathbf{M}^{\mathbf{W}}$というマスク行列の積が狭義下三角行列になっていれば良いということになります。このために$\mathbf{M}^{\mathbf{W}}$ならびに$\mathbf{M}^{\mathbf{V}}$の満たすべき条件は以下のようになります。
隠れ層が$K$次元である場合に$1, \ldots, K$をランダムに並べ替えたインデックスのベクトル$m(k)$を用意します。これを用いて$\mathbf{M}^{W}$ならびに$\mathbf{M}^{\mathbf{V}}$は以下のように書けます。
$$ M_{k,d}^{\mathbf{W}} = \begin{cases} 1 & \mathrm{if} \quad d \leq m(k) \\ 0 & \mathrm{otherwise} \end{cases} $$
$$ M_{d,k}^{\mathbf{V}} = \begin{cases} 1 & \mathrm{if} \quad m(k) < d \\ 0 & \mathrm{otherwise} \end{cases} $$
このマスク行列の積が本当に狭義下三角行列になるのか疑わしいと思った方は、以下のコードをお試しください。
import numpy as np
D = 3
K = 5
M_W = np.zeros((K, D))
M_V = np.zeros((D, K))
m = np.random.permutation(np.arange(K))
for k in range(K):
M_W[k, :m[k]+1] = 1.0
M_V[m[k]+1:, k] = 1.0
print(np.dot(M_V, M_W))
# Output:
# [[0. 0. 0.]
# [1. 0. 0.]
# [2. 1. 0.]]
上記は、1層しか隠れ層を持ちませんが、これを多層のニューラルネットワークに拡張する方法についても論文に触れられています。詳細の説明は割愛いたしますが、以下に示す実装例ではそちらを使用していますので、論文を読みつつ、そちらと合わせてご参照いただければと思います。
さて、以上から、自己回帰といっても、必ずしも各次元を順々に評価していく必要はなく、使い方如何では効率的に評価することがかのであることが分かりました。一方で、この自己回帰モデルの逆変換を行うためには、
$$ y_t = h^{-1}(z_t; \Theta(\mathbf{y}_{1:t-1})) $$
のような式を評価する必要があり、常に$y_1$から順に評価をしていく必要があることから、うまく並列化することができません。
それ故、深層学習を用いる場合においては、より時間のかかる訓練を効率化することに重点をおく必要があります。以下で紹介するInverse Autoregressive Flow (IAF) [1]とMasked Autoregressive Flow (MAF) [2]は、上記の自己回帰的な変換を$\mathbf{y}$から$\mathbf{z}$への変換$\mathbf{f}$あるいは、その逆変換$\mathbf{g} = \mathbf{f}^{-1}$に用いた手法で、いずれも上記のMADEを用いて自己回帰モデルを構成しています。
IAFは変分推論、MAFは密度推定のための手法ですが、それぞれの訓練法に着目して、その違いについてみていきたいと思います。
Inverse Autoregressive Flow (IAF)
IAFは、その論文のタイトルに「Variational Inference」とある通り、変分推論にAutoregressive Flowを用いた手法です。
第1回でご説明した通り、変分推論にNormalizing Flowを使った場合の式は、
$$ \mathbb{E}_{\mathbf{z} \sim p_Z(\mathbf{z})} \left[ \log p(\mathbf{x}, \mathbf{g}(\mathbf{z}; \theta)) - \log p_Z(\mathbf{z}) \right] $$
というエネルギー関数を最大化するのが目的なのでした。この式を評価するためにはnormalizingとは逆方向にサンプルが簡単な確率変数$\mathbf{z}$をより複雑な確率密度に従う確率変数$\mathbf{y}$に変換する必要があります。ですから、訓練においては、この「normalizingとは逆方向の変換」を効率的に評価できる方が嬉しいです。
そこで、先ほどの自己回帰モデルを$\mathbf{z}$から$\mathbf{y}$への変換$\mathbf{g}$に適用します。このようにNormalizing Flowの逆変換に自己回帰モデルを用いるのでInverse Autoregressive Flowという名前がついています。
Masked Autoregressive Flow (MAF)
IAFとは対照的に、MAFはその論文のタイトルには「Density Estimation」とあり、MAFが確率密度推定のための手法であることが分かります。
確率密度推定においては既知の確率密度を持つ確率変数$\mathbf{z} \sim p_Z(\mathbf{z})$をNormalizing Flowの逆変換により確率密度が未知ながらサンプルだけは得ることができるような確率変数$\mathbf{y}$に変換するのでした。
この変換をニューラルネットで表現した際には、サンプル$\mathbf{y}$を変数変換して得られた$\mathbf{z}$に対して尤度最大化問題を得ことでネットワークを訓練します。従って以下の対数尤度の評価が効率的に行える必要があります。
$$ \log p_Y(\mathbf{y}) = \log p_Z(\mathbf{f}(\mathbf{y})) + \left| \frac{\partial \mathbf{f}}{\partial \mathbf{y}} \right| $$
ですから、MAFにおいては、IAFとは反対にnormalizing方向、すなわち$\mathbf{y}$を$\mathbf{z}$に変換する関数$\mathbf{f}$が効率的に評価できれば、訓練をより効率的に行えることが分かります。
実装例 (MAF)
以下ではMADEによる変換パラメータの推定と、それを用いたMAFの変換であるAutoregressiveTransfromの実装例を示しています。
MADEを各変換でそのまま利用してしまうと次元のインデックスによって表現力に差が出てしまうので、MAFの各層では次元の順序をランダムに入れ替えてMADEを適用した後に元に戻すということをしています。
口説いですが、全体の実装を確認したい方は、私のGitHubの方をご確認ください。
https://github.com/tatsy/normalizing-flows-pytorch
MADE
class MADE(nn.Module):
def __init__(self, in_out_features, num_hidden=2, base_filters=32, use_companion=False):
super(MADE, self).__init__()
self.in_out_chs = in_out_features
self.num_hidden = num_hidden
self.base_filters = base_filters
self.use_companion = use_companion
self.masks = None
weights = []
biases = []
units = []
bnorms = []
hidden_dims = [in_out_features] + [base_filters] * num_hidden
for in_dims, out_dims in zip(hidden_dims[:-1], hidden_dims[1:]):
xavier_scale = np.sqrt(2.0 / (out_dims + in_dims))
W = torch.randn(out_dims, in_dims) * xavier_scale
U = torch.randn(out_dims, in_dims) * xavier_scale
b = torch.randn(out_dims) * 0.01
weights.append(nn.Parameter(W))
units.append(nn.Parameter(U))
biases.append(nn.Parameter(b))
bnorms.append(nn.BatchNorm1d(out_dims))
xavier_scale = np.sqrt(2.0 / (in_out_features + hidden_dims[-1]))
W = torch.randn(in_out_features, hidden_dims[-1]) * xavier_scale
U = torch.randn(in_out_features, hidden_dims[-1]) * xavier_scale
b = torch.randn(in_out_features) * 0.01
weights.append(nn.Parameter(W))
units.append(nn.Parameter(U))
biases.append(nn.Parameter(b))
self.weights = nn.ParameterList(weights)
self.bnorms = nn.ModuleList(bnorms)
self.biases = nn.ParameterList(biases)
if use_companion:
self.units = nn.ParameterList(units)
def forward(self, z):
self._create_masks()
for i in range(self.num_hidden):
self.masks[i] = self.masks[i].type_as(z).to(z.device)
h = F.linear(z, self.weights[i] * self.masks[i], self.biases[i])
if self.use_companion:
h += F.linear(torch.ones_like(z), self.units[i] * self.masks[i])
z = torch.relu(self.bnorms[i](h))
self.masks[-1] = self.masks[-1].type_as(z).to(z.device)
h = F.linear(z, self.weights[-1] * self.masks[-1], self.biases[-1])
if self.use_companion:
h += F.linear(torch.ones_like(z), self.units[-1] * self.masks[-1])
return h
def _create_masks(self):
m_prev = torch.arange(self.in_out_chs)
hidden_dims = [self.in_out_chs] + [self.base_filters] * self.num_hidden
masks = []
for in_dims, out_dims in zip(hidden_dims[:-1], hidden_dims[1:]):
min_k = min(m_prev.min().item(), self.in_out_chs - 2)
m = torch.from_numpy(np.random.randint(min_k, self.in_out_chs - 1, size=(out_dims)))
M = torch.zeros(out_dims, in_dims)
for k in range(out_dims):
M[k, :] = (m_prev <= m[k]).float()
masks.append(M)
m_prev = m
M = torch.zeros(self.in_out_chs, hidden_dims[-1])
m = m_prev
for k in range(hidden_dims[-1]):
M[m[k] + 1:, k] = 1.0
masks.append(M)
self.masks = masks
MAF
class AutoregressiveTransfrom(nn.Module):
def __init__(self, in_out_features, num_hidden=3, base_filters=32):
super(AutoregressiveTransfrom, self).__init__()
self.in_out_chs = in_out_features
perm = torch.eye(in_out_features)[:, torch.randperm(in_out_features)]
self.register_buffer('perm', perm)
self.net_s = MADE(in_out_features, num_hidden, base_filters)
self.net_t = MADE(in_out_features, num_hidden, base_filters)
self.register_parameter('s_log_scale', nn.Parameter(torch.randn(1) * 0.01))
self.register_parameter('s_bias', nn.Parameter(torch.randn(1) * 0.01))
def forward(self, z, log_df_dz):
z = torch.mm(z, self.perm)
s = torch.tanh(self.net_s(z)) * self.s_log_scale + self.s_bias
t = self.net_t(z)
z = z * torch.exp(s) + t
log_df_dz += torch.sum(s, dim=1)
return z, log_df_dz
def backward(self, z, log_df_dz):
m = torch.zeros(self.in_out_chs).type_as(z).to(z.device)
for i in range(self.in_out_chs):
s = torch.tanh(self.net_s(z)) * self.s_log_scale + self.s_bias
t = self.net_t(z)
z[:, i] = ((z - t) * torch.exp(-s))[:, i]
log_df_dz -= s[:, i]
m[i] = 1.0
z = torch.mm(z, self.perm.t())
return z, log_df_dz
実験結果
実験結果の印象ですが、MAFは実装が結構細かくて、MADEも途中にBatch Normalizationを入れるか、活性化関数に何を使うかなどで結構結果が大きく変わりました。
その割にはReal NVPと比べてそこまで良い結果が出ているわけではないので、シンプルな実装ながら、高い表現力を出すことができるReal NVPやBijective Couplingのアイディアはやはり強力だと思いました。
MAF
| 目的の分布 | 再現された分布 | GIF (画像をクリック) |
|---|---|---|
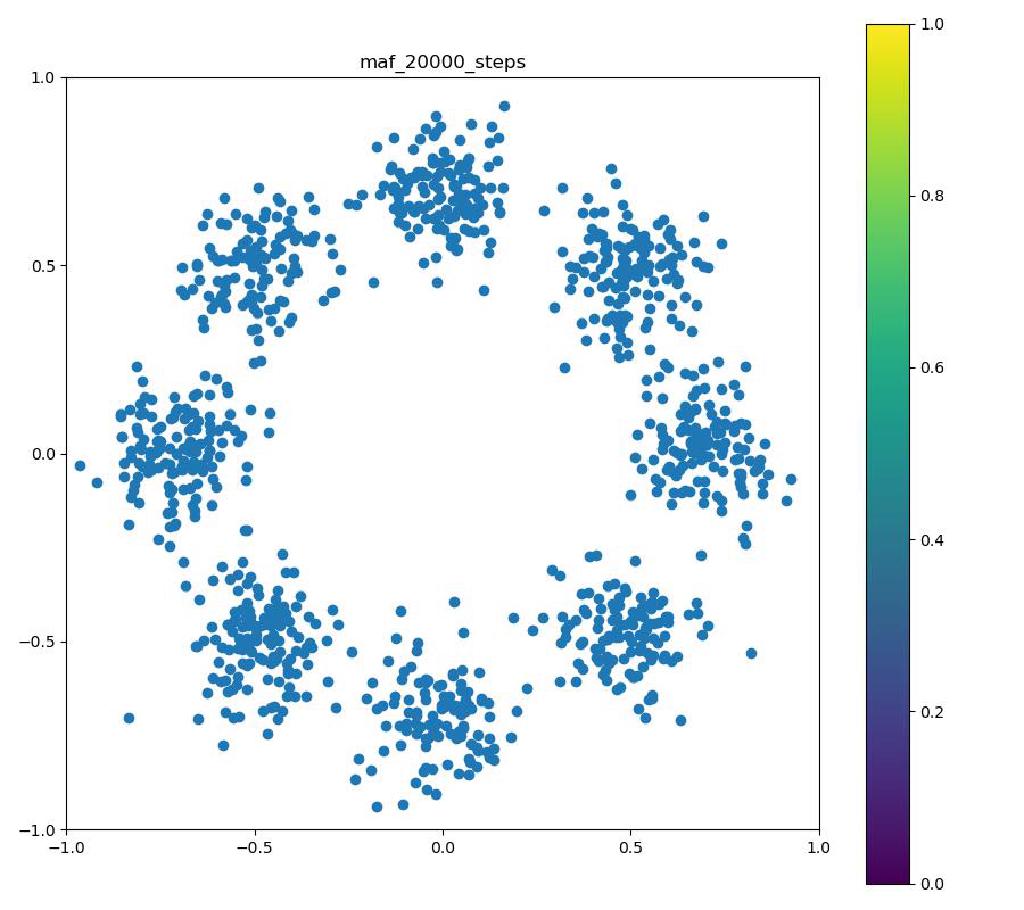 | 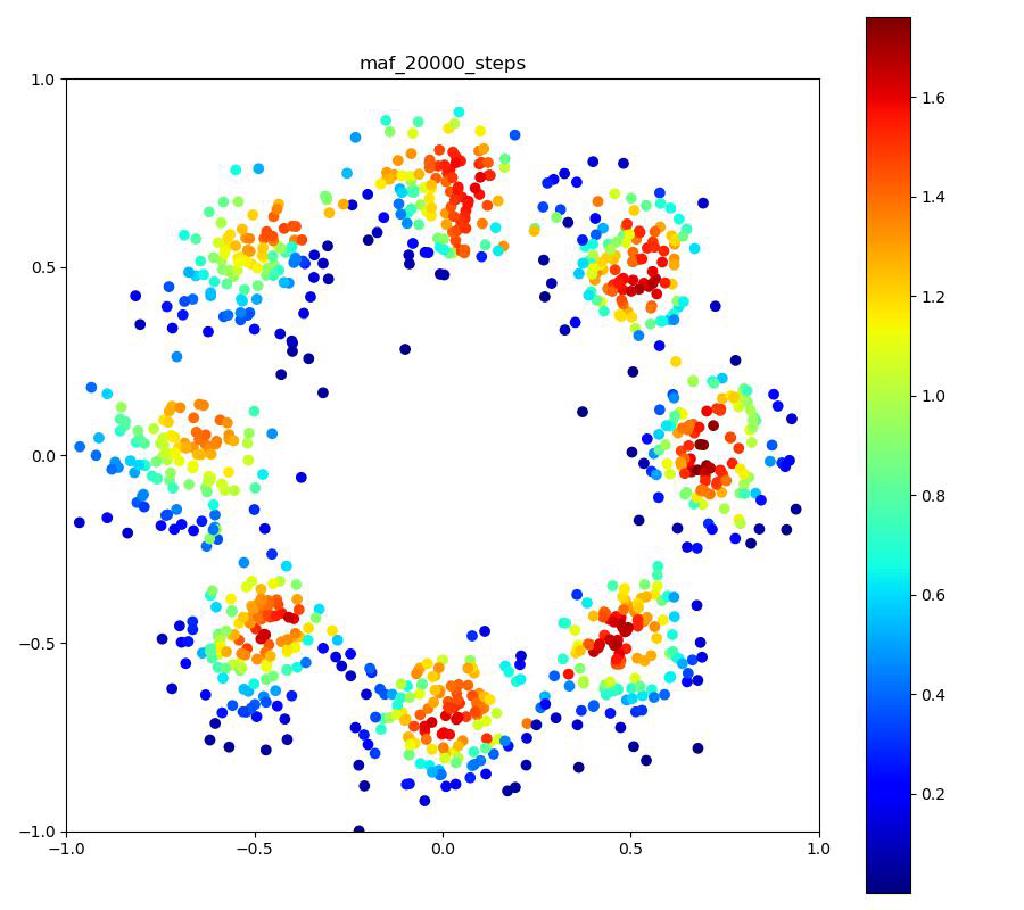 | 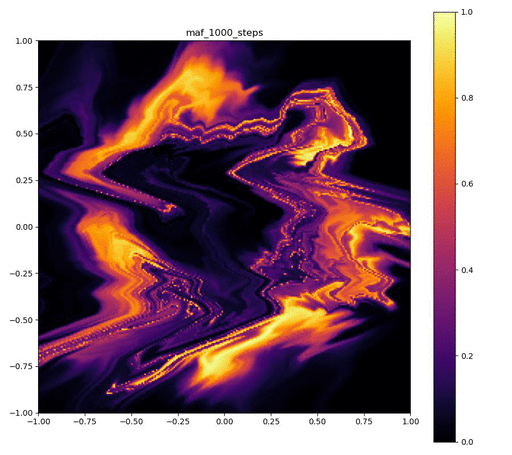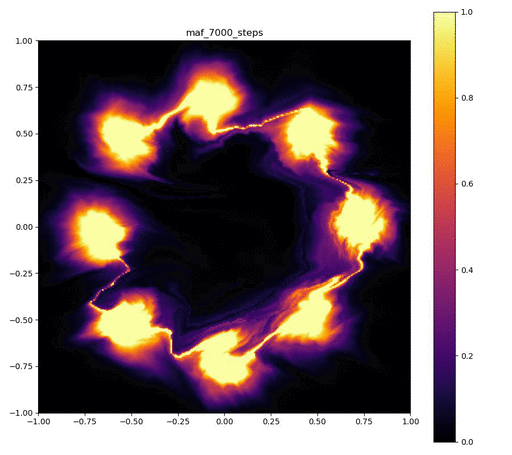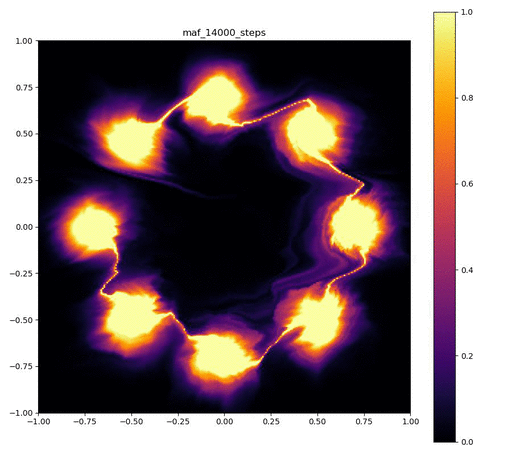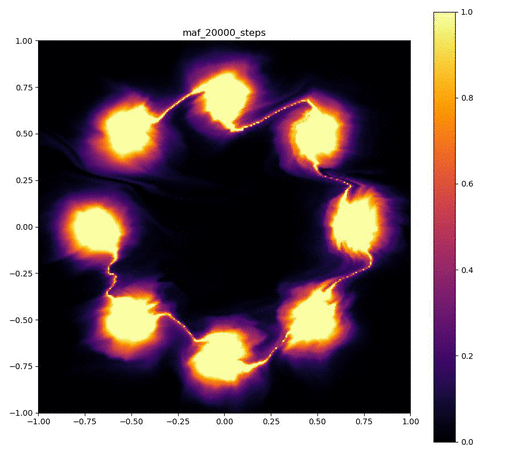 |
まとめ
今回は自己回帰モデルによってFlowを表現するIAFならびにMAFについてご紹介しました。
これら二つの方法では、従来のニューラルネットにおいて、重み係数を適切にマスクすることで、大きく処理を変えることなく自己回帰モデルを実現するMADEが使われている一方、その逆変換が効率的に評価できないことから、変分推論と密度推定というIAFとMAFの目的の違いから、定式化が変わることをご説明いたしました。
次回は、Normalizing Flowの新しい潮流?であるInvertible Residual Networkと、それを用いたNormalizing FlowであるResidual Flowについてご紹介したいと思います。
参考文献
[1] Kingma et al., “Improved Variational Inference with Inverse Autoregressive Flow,” NIPS 2016. [arXiv]
[2] Papamakarios et al., “Masked Autoregressive Flow for Density Estimation,” NIPS 2017. [arXiv]
[3] Germain et al., “MADE: Masked Autoencoder for Distribution Estimation,” ICLR 2015. [arXiv]
