Normalizing Flow入門第6回 Residual Flow

Tatsuya Yatagawa

2021-01-16

こんにちはtatsyです。Normalizing Flow入門(?)の第6回です。

今回はNormalizing Flowの中でも逆関数が計算可能なニューラルネットワークのレイヤーを使うInvertible Residual Network[1]と、その発展系であるResidual Flow[2]について見ていきたいと思います。

個人的に、この論文は論理の運び方に無駄がなく、学部生レベル＋αくらいの線形代数の知識があれば全体を理解できる、とても面白い論文だと思いました。ただし、実用的には使いづらいのでは？という部分もあるので、そのあたりも合わせてご紹介していきたいと思います。

Invertible Residual Network (iResNet)

Invertible, すなわち逆関数を持つ(かつ、容易に評価できる)ニューラルネットワークの考え方は、これからお話しするiResNet[1]の著者の一人であるJacobsenらが2018年に発表したInvertible Deep Networks[3] (iRevNet, 表記が似ているので注意)という論文に端を発しているようです。

この論文の提案しているiRevNetはReal NVPのように入力のベクトルを2つのグループに分割して、片方を変換するパラメータを他方から求めるということをしており、論文内でもNICEやReal NVPとの関係性が言及されています。

このiRevNetをResidual Network拡張したものが端的にはiResNetなのですが、iResNetは逆関数やヤコビアンの計算方法が、ネットワークの細かな調整ではなく数学的な背景に裏打ちされている部分が面白いところです。

iResNetは、通常のResNetと同じく以下の形で入力変数$\mathbf{y}$を出力変数$\mathbf{z}$に変換します。

$$ \begin{equation} \mathbf{z} = \mathbf{f}(\mathbf{y}) = \mathbf{y} + \mathbf{g}(\mathbf{y}) \label{eq:resnet} \end{equation} $$

この逆変換を書き下すと

$$ \begin{equation} \mathbf{y} = \mathbf{z} - \mathbf{g}(\mathbf{y}) \label{eq:inv-resnet} \end{equation} $$

となりますが、この計算も$\mathbf{g}$に採用するネットワークを一例としてBijective Coupling等にすれば逆関数のみならず、変換のヤコビアンについても計算可能でしょう。その一方でiResNetは$\mathbf{g}$を構成するレイヤーが通常の全結合層や畳み込み、バッチ正規化、活性化関数などから成るネットワークで良い、というのが優れているところです。

ネットワークの逆変換

まず、ネットワークの逆変換ですが、これを一般的なネットワークにより定義される$\mathbf{g}$に対して実現するためにバナッハの不動点定理を用います。以下では、ベクトル空間の定義や写像の細かい条件などは省いて説明しますので、その点はご了承ください。

バナッハの不動点定理は、縮小写像$\mathbf{f}$をとあるベクトル$\mathbf{x}$に何度も適用していくと、とある点$\mathbf{x}_t = \mathbf{f}(\mathbf{x}_{t+1})$で与えられるベクトル列が1点に収束することを表した定理です。

ここで縮小写像とは、とある写像$\mathbf{f}$が与えられた時、任意のベクトルの組$\mathbf{x}$, $\mathbf{y}$について、$\mathbf{f}(\mathbf{x})$と$\mathbf{f}(\mathbf{y})$の距離が$\mathbf{x}$と$\mathbf{y}$の距離よりも小さくことを言います。これをよりフォーマルに$\alpha < 1$を用いて

$$ \| \mathbf{f}(\mathbf{x}) - \mathbf{f}(\mathbf{y}) \| \leq \alpha \| \mathbf{x} - \mathbf{y} \| $$

と書きます。この時、定数$\alpha$は距離の減少率の上界で、これをリプシッツ定数と呼ぶのでした。

今、式\eqref{eq:inv-resnet}において、$\mathbf{g}$が縮小写像であるとして、そのリプシッツ定数を$\beta < 1$とします。また、$\mathbf{g}$を用いて、数列$\mathbf{y}^{t}$を

$$ \mathbf{y}^{t} = \mathbf{z} - \mathbf{g}(\mathbf{y}^{t-1}) $$

と定義することにします。すると$\mathbf{y}^{t}$は$\mathbf{g}$が縮小写像の時に限り$\mathbf{y}$に収束します。これを証明するために、$\mathbf{y}^{t}$と真の$\mathbf{y}$の距離がどうなるかをみてみます。

$$ \begin{aligned} \| \mathbf{y} - \mathbf{y}^{t} \| &= \left\| (\mathbf{z} - \mathbf{g}(\mathbf{y})) - (\mathbf{z} - \mathbf{g}(\mathbf{y}^{t-1})) \right\| \nonumber \\ &= \left\| \mathbf{g}(\mathbf{y}) - \mathbf{g}(\mathbf{y}^{t-1}) \right\| \nonumber \\ & \leq \beta \left\| \mathbf{y} - \mathbf{y}^{t-1} \right\| \nonumber \\ & \qquad \vdots \nonumber \\ & \leq \beta^{t} \left\| \mathbf{y} - \mathbf{y}^{0} \right\| \\ \end{aligned} $$

従って、この両辺で$t \rightarrow \infty$の極限を取ると、$\beta < 1$であることから

$$ \| \mathbf{y} - \mathbf{y}^{\infty} \| = 0 $$

となることが分かります。

以上の議論からニューラルネットにより定義される$\mathbf{g}$のリプシッツ定数が1より小さい時には、適当な$\mathbf{y}^{0}$をスタートとして繰り返し$\mathbf{z} - \mathbf{g}(\mathbf{y}^{t})$を評価することで$\mathbf{y}$が得られることが分かります。ここでの必要条件はネットワークのリプシッツ定数が1より小さいことだけなので、ネットワーク自体がどのように構成されているかはさほど重要ではありません。

ニューラルネットは複数の関数の合成だと捉えることができますが、合成関数のリプシッツ定数が1を下回るためには、合成される各関数全てのリプシッツ定数が1以下になれば十分です。そこで、ニューラルネットを全結合層や畳み込み層と活性化関数のみで構成します。よく使われる活性化関数 (sigmoid, tanh, ReLUなど)はいずれもリプシッツ定数が1以下なので、全結合層、ならびに畳み込み層のリプシッツ定数が1未満であれば、全体としてはリプシッツ定数が1未満になります。

全結合層や畳み込み層のリプシッツ定数を制約するためにGAN（Generative Adversarial Networks)の分野で紹介されているSpectral Normalizationを用います。Spectral NormalizationはGANの分野で生成器(Generator)と判別器(Discriminator)がそれぞれ有限のリプシッツ定数を持つ方が良い画像が作れる、という理解に基づいて提案されたものです。

名前にSpectral Normとあるのは、全結合層や畳み込み層が実際には行列の掛け算で定義されており、その行列のスペクトル・ノルム(=絶対値が最大固有値)の大きさが1になるようにレイヤーのパラメータを正規化するためです。

今回のiResNetでは全結合層ならびに畳み込み層はリプシッツ定数が1未満である必要があり、リプシッツ定数がより小さい分には問題がないので、Spectral Normalizationを少し改良し、絶対値最大固有値が1未満の定数$c$より大きい時に限ってその値が$c$になるように正規化をを行います。

このSpectral Normalizationの実装例は以下のURLからご確認ください。

https://github.com/tatsy/normalizing-flows-pytorch/blob/master/flows/spectral_norm.py

以上の操作により、一般的なニューラルネットの構成に対して、逆関数に相当する演算が行えることが分かりました。

ネットワークのヤコビアン

それでは次にネットワークのヤコビアンを求める方法について考えます。式\eqref{eq:resnet}の定義に従えば、ResNetの関数$\mathbf{f}$のヤコビ行列$\mathbf{J}_\mathbf{f}$は次のようにかけるはずです。

$$ \mathbf{J}_{\mathbf{f}} = \mathbf{I} + \mathbf{J}_{\mathbf{g}} $$

この時、$\mathbf{g}$のリプシッツ定数が1未満であったことから、そのヤコビアンの絶対値最大固有値の大きさも1未満(つまり-1よりは大きい)であり、従って$\mathbf{J}_{\mathbf{f}}$が正定値行列になることが分かります。

よってヤコビアン、すなわちヤコビ行列の行列式には以下の関係が成り立ちます。

$$ \det \left| \mathbf{J}_\mathbf{f} \right| = \det \mathbf{J}_\mathbf{f} $$

次に、実際に密度推定に必要なのはヤコビアンの対数なので、両辺の対数をとります。

$$ \log \det \left| \mathbf{J}_\mathbf{f} \right| = \log \det \mathbf{J}_\mathbf{f} $$

今、行列指数$\exp \mathbf{A}$の逆変換として$\log \mathbf{A}$を定義したとすると、次のような関係式が成り立つことが知られています。

$$ \log \det \mathbf{A} = \mathrm{tr} \left( \log \mathbf{A} \right) $$

なお、上記の行列指数ならびに行列対数は行列の要素に対して個別に、指数・対数をとったものとは異なっていることに注意してください。この関係式を用いると、

$$ \log \det \left| \mathbf{J}_\mathbf{f} \right| = \mathrm{tr} \left( \log \mathbf{J}_\mathbf{f} \right) = \mathrm{tr} \left( \log ( \mathbf{I} + \mathbf{J}_\mathbf{g} ) \right) $$

という結果が得られます。ここで、行列対数$\log (\mathbf{I} + \mathbf{J}_{\mathbf{g}})$を$\mathbf{J}_{\mathbf{g}}$についてマクローリン展開すると、

$$ \frac{\mathbf{J}_{\mathbf{g}}}{1} - \frac{\mathbf{J}_{\mathbf{g}}^2}{2} + \frac{\mathbf{J}_\mathbf{g}^3}{3} - \cdots = \sum_{k=1}^{\infty} (-1)^{k+1} \frac{\mathbf{J}_\mathbf{g}^{k}}{k} $$

となるので、行列和のトレースが各行列のトレースの和に等しいことに注意すると、

$$ \log \det \left| \mathbf{J}_\mathbf{f} \right| = \sum_{k=1}^{\infty} (-1)^{k+1} \frac{\mathrm{tr} (\mathbf{J}_\mathbf{g}^{k})}{k} $$

という式が得られます。この式において、$\mathbf{J}_\mathbf{g}$の固有値の絶対値は$1$より小さかったので、$k$が十分に大きい項では、$J_{\mathbf{g}}^k$のトレースが十分小さくなっていることが予想できます。

従って、$k$を適当な有限の範囲で打ち切ってあげることで、ResNetにより定義される変換のヤコビアンについても効率的に計算できそうです。

Hutchinsonのトレース推定法

ところが、実際にはトレースを求めるためにネットワークのヤコビアン$\mathbf{J}_\mathbf{g}$を評価する必要があり、さらにこれが級数の中に入っていることからも、それほど効率的な計算は望めません。

そこでiResNetではトレースを正確に計算することは諦めて、確率的に期待値が行列のトレースとなるような計算方法を用います。もし期待値が正しくトレースの値を取るのであれば、訓練時には確率的最急降下法の勾配の期待値も本来欲しい勾配を期待値とするはずなので、より効率的に訓練が行えるというわけです。

このような確率的なトレースの計算法としてHutchinsonのトレース推定法という手法が用いられています。これはトレースの性質から以下のような式変形を経て導出されます。

$$ \begin{aligned} \mathrm{tr} \mathbf{A} &= \mathrm{tr} (\mathbf{A} \mathbf{I}) \\ &= \mathrm{tr} (\mathbf{A} \mathbb{E}(\mathbf{u}^T \mathbf{u})) \\ &= \mathrm{tr} (\mathbf{u}^T \mathbf{A} \mathbf{u}) \\ &= \mathbb{E} [\mathrm{tr}~(\mathbf{u}^{T} \mathbf{A} \mathbf{u})] \\ &= \mathbb{E} [\mathbf{u}^{T} \mathbf{A} \mathbf{u}] \end{aligned} $$

この式で$\mathbf{u}$はその共分散行列が単位行列$\mathbf{I}$になるような確率変数で、例えば標準正規分布に従うような多次元ベクトルなどがそれに相当します。

したがって、多次元正規分布から$\mathbf{u}$を何個かサンプルして、その$\mathbf{u}$の行列$\mathbf{J}_{\mathbf{g}}$に対する二次形式を計算できれば良いことになります。

今、$\mathbf{J}_{\mathbf{g}}$を評価するには、行列の行数回だけネットワークを評価する必要がありますが、$\mathbf{u}^T \mathbf{J}_{\mathbf{g}}$のような行列ベクトル積の計算は$\mathbf{u}$をネットワークに逆伝搬する計算と等価なので、必要なネットワークの評価(に相当する計算)は1回きりです。

このことから、Hutchinsonのトレース推定法を用いることで、確率的ではあるものの、より効率的にヤコビ行列のトレースを計算できることが分かります。

以上の議論から、式\eqref{eq:resnet}に示したResNetのようなネットワークを用いて、Normalizing Flowに必要な計算を効率的に行うことができます。

Residual Flow

さて、iResNetを導入したことでNormalizing Flowの構成に重要となる逆関数の計算とヤコビアンの計算が「計算時間の上では」効率的に行えることが分かりました。ですが、iResNetを実際にNormalizing Flowに適用する場合には2つの問題点があります。

1つ目は、ヤコビアンを求めるときの無限級数の打ち切りです。この打ち切りは、上記の通り影響は少ないと仮定できるものの、高い精度を実現するにはそれ相応の項数を取る必要があることから、計算時間と精度のトレードオフが発生してしまいます。

2つ目に、ニューラルネットの学習において、上記のような級数の計算をしてしまうと、誤差逆伝搬のために必要なネットワークの計算グラフが巨大になってしまい、結果多大なメモリを必要とすることになっていまいます。

このような問題を防ぐため、Residual Flowでは、特に訓練時に有効な確率的なヤコビアンの評価法と、省メモリな誤差逆伝搬の方法を提案しています。

確率的なヤコビアン計算

iResNetにおいてヤコビアンを「直接的に」計算するとすると、計算量が特に大きいのは、変換関数$\mathbf{g}$のトレースを求める処理と、無限級数の和を取る処理に分けられます。

iResNetではHutchinsonのトレース推定法を導入することで前者の行列トレースの計算を効率化しましたが、Residual Flowでは後者の無限級数をとる計算も確率的に行うことで効率化を図ります。

今、無限級数の各項を加算するかどうかを0項目から順にコイントスで決めていくことにします。コインを投げて裏がでたらその項を足して、次の項のコインとするに写るけれど、一度表がでたら、そこで級数の加算を打ち切る、という具合です。

このようなコイントスで裏(あるいは表)がでたら試行を継続するというような確率モデルはベルヌーイ試行と呼ばれていて、$k$回目のコイントスで裏がでて試行が打ち切られる確率は、コインで表が出る確率を$p$として$p (1 - p)^{k-1}$で表せます。この確率は試行回数を離散的な確率変数$N$とする幾何分布$P(N = k)$に対応しています。

無限級数を評価するにあたり、このようなベルヌーイ試行で項を足すかどうかを決めていく場合、$k$項目が加算される確率は、和が取られる項の総数$N$が$k$以上である確率に相当します。

これを幾何分布を用いて表すとすると、試行が$k$回以上続く、ということは$k-1$回目目でで一度も表がでない、ということに相当するので、その確率$P(N \geq k) = (1 - p)^{k-1}$となります。

このことから、加算される項の数$n$を幾何分布$P(N)$からサンプルすることで、以下の式により確率的に無限級数が計算できます。

$$ \begin{equation} \log \det \left| \mathbf{J}_\mathbf{f} \right| = \mathbb{E}_{n \sim P(N), \mathbf{u} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})} \left[ \sum_{k=1}^{n} \frac{(-1)^{k+1}}{k} \frac{(\mathbf{u}^{T} \mathbf{J}_\mathbf{g}^{k}) \mathbf{u}}{P(N \geq k)} \right] \label{eq:infinite-series} \end{equation} $$

なお、ここで「確率的に」といっているのは、無限に確率変数のサンプルをとった時に、そのサンプルから求まる平均値が、実際の期待値に十分に近くなることを指します。

このような確率的な計算を用いることで1回1回の評価に用いるサンプル数を少なくし、処理を効率化したとしても、訓練を長く続けていくことで、上記のHutchinsonのトレース推定法を用いた場合と同様、確率的最急降下法において正しい勾配を期待値として得られるわけです。

省メモリな誤差逆伝搬

次に省メモリな誤差逆伝搬について、ご紹介します。前述の通り、元々のiResNetでは、ヤコビアンを計算するために無限級数和の項同士を加算して行った結果、計算グラフが大きくなってしまうことがメモリを大きく消費する原因なのでした。

この問題を防ぐためにResidual Flowでは、パラメータによる誤差関数の計算方法を自動微分に頼らない方法に部分的に変更します。今、ある層のパラメータを$\Theta$と置くと、その層からは$\mathbf{z}$とヤコビアンの対数$\log \det \mathbf{J}_{\mathbf{f}}$が出力されているはずです(本来は層の番号などを添字に取るべきですが、今回は省略します)。

この時、出力の$\mathbf{z}$とヤコビアンの対数$\log \det \mathbf{J}_{\mathbf{f}}$はいずれもパラメータ$\Theta$に依存しています。また、最終的に計算されるエネルギー関数を$\mathcal{L}$と表記することにすると、$\mathcal{L}$は$\mathbf{z}$と$\log\det J_{\mathbf{f}}$の両方に依存しているので、$\mathcal{L}$を$\Theta$で偏微分すると、合成関数の微分則から以下のように書けます。

$$ \frac{\partial \mathcal{L}}{\partial \Theta} = \frac{\partial{L}}{\partial\mathbf{z}} \cdot \frac{\partial \mathbf{z}}{\partial \Theta} + \frac{\partial{L}}{\partial \log\det \mathbf{J}_{\mathbf{f}}} \cdot \frac{\partial \log\det J_{\mathbf{f}}}{\partial \Theta} $$

通常の誤差逆伝搬では、あるレイヤーの出力での誤差関数の偏微分、すなわち$\partial\mathcal{L} / \partial\mathbf{z}$と$\partial\mathcal{L} / \partial\log\det \mathbf{J}_{\mathbf{f}}$が上の層から逆伝搬されてくるので、各層で計算しなければならないのは$\partial\mathbf{z} / \partial\Theta$と$\partial\log\det \mathbf{J}_{\mathbf{f}} / \partial\Theta$の部分だけです。

これを計算グラフに頼った誤差逆伝搬で計算する時には、特に$\partial\log\det \mathbf{J}_{\mathbf{f}} / \partial\Theta$の計算について膨大な計算グラフを逆にたどっていく必要が出てきます。ですが、式\eqref{eq:infinite-series}を用いて、この偏微分を計算してみると$\Theta$に依存しているのはヤコビ行列の部分だけなので、以下のように書き直すことができます。

$$ \frac{\partial\log\det \left| \mathbf{J}_\mathbf{f} \right|}{\partial\Theta} = \mathbb{E}_{n \sim P(N), \mathbf{u} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})} \left[ \sum_{k=1}^{n} \frac{(-1)^{k+1}}{P(N \geq k)} \mathbf{u}^{T} \mathbf{J}_{\mathbf{g}}^{k-1} \frac{\partial \mathbf{J}_{\mathbf{g}}}{\partial\Theta} \mathbf{u} \right] $$

Residual Flowの論文では$n$の範囲を取り直して、次の形で書き直しています。このとき$P(N = 0) = 1$なので$P(N)$の定義域が1以上になっていることに注意してください(そうでないと和を取る範囲が$n-1$までにならないとおかしい)。

$$ \begin{equation} \frac{\partial\log\det \left| \mathbf{J}_\mathbf{f} \right|}{\partial\Theta} = \mathbb{E}_{n \sim P(N), \mathbf{u} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})} \left[ \left( \sum_{k=0}^{n} \frac{(-1)^{k}}{P(N \geq k)} \mathbf{u}^{T} \mathbf{J}_{\mathbf{g}}^{k} \right) \frac{\partial \mathbf{J}_{\mathbf{g}}}{\partial\Theta} \mathbf{u} \right] \label{eq:neumann-series} \end{equation} $$

この計算は、対数ヤコビアンの計算の時と同様に$\mathbf{u}^{T} \mathbf{J}_{\mathbf{g}}^{k}$の部分は自動微分による勾配計算を繰り返すだけでよく、ネットワークの評価回数は$k$回で済みます。問題は$\partial\mathbf{J}_{\mathbf{g}} / \partial\Theta$の部分ですが、この部分に関しては、通常通りの自動微分による計算が必要なので「計算時間の観点」で言えば、効率的にすることは難しいです。

ですが、この$\partial\mathbf{J}_{\mathbf{g}} / \partial\Theta$の部分は、誤差逆伝搬で誤差関数に対する勾配を受け取らずとも計算が可能な部分なので、これをネットワークを順方向に評価していく時に、一緒に評価してしまいます。一度、この評価が終われば無限級数の計算で生じた大きな計算グラフはもう必要ありませんので、これにより大幅にメモリが節約できる、というわけです。

LipSwish

Residual Flowでは、学習をより安定的に行うための活性化関数についても提案しています。それがLipSwishと呼ばれるものです。元々iResNetでは、勾配計算を安定的に行うためにReLUのような導関数が不連続となるものではなく、ELUやSoftplusのように導関数も連続となる活性化関数を使うのが良い、とされていました。

一方で、Normalizing Flowの学習ではエネルギー関数はヤコビアン、すなわち関数の1階微分により定義されます。さらにこの誤差関数を微分してパラメータ更新のための勾配を得るので、結果的には関数の2階微分を評価する必要が出てきます。

ところが、例えばELUを用いる場合には、ELUの2階微分は入力が0以上の箇所で0になってしまうため、勾配消失と同じような問題が起こってしまい、学習の効率があがりません。特にELUの0以上の箇所というのはリプシッツ定数が1で最大を取る箇所なので、出力の変化量が大きいにも関わらず、勾配が焼失してしまうのはあまり効率的ではありません。

以上の議論から、理想的な活性化関数は次の2つの条件を満たせば良いことが分かります。

関数の1階微分が0にならない (例: sigmoid, tanhなど)
1階微分が1に近い箇所、つまりできる限りリプシッツ定数が大きい箇所で2階導関数が大きな値を取る

このような性質を満たす活性化関数として、Residual FlowではLipSwish関数が提案されています。

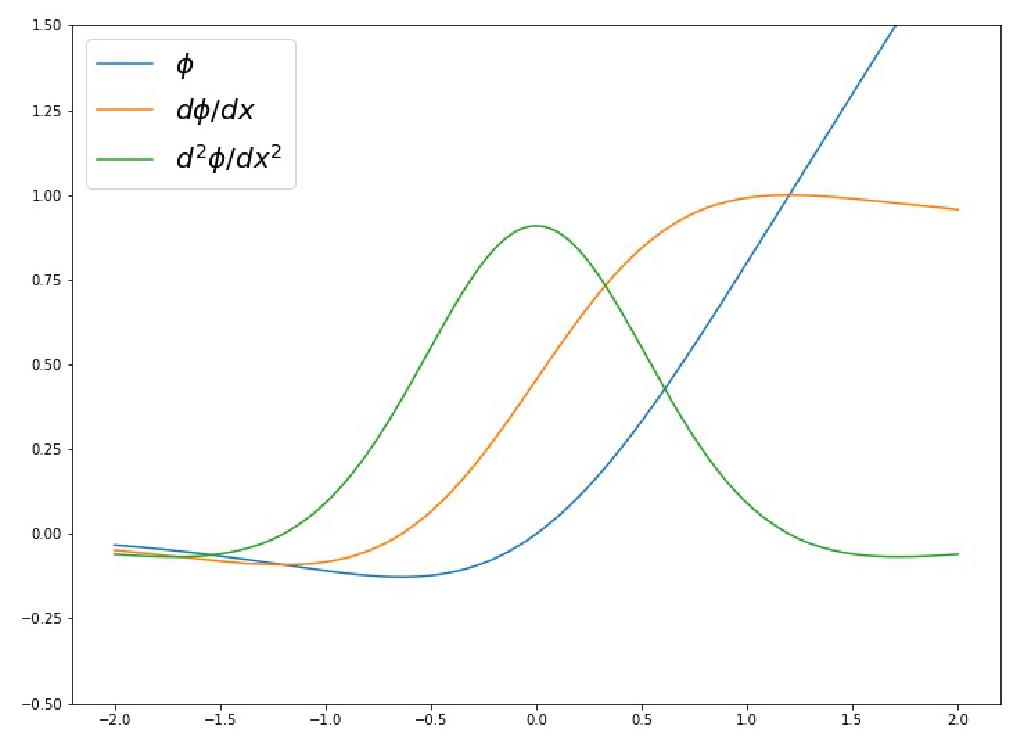
$$ \mathrm{LipSwish}(z) = z \cdot \sigma(\beta z) / 1.1 $$

LipSwishと、その1階、2階導関数は以下のようなグラフとなっており、1階導関数が大きな値を取る場所でも2階導関数がはっきり0以外の値をとっています。なお、LipSwishにおいて$\beta$はパラメータなので、これは学習時に更新をしてあげる必要があります。

実装例

Residual Flowは今回の記事の分量からも分かる通り、それなりのコード量になりますので、主要箇所のみ実装例を示します。詳細については以下のGitHubからご確認いただければ幸いです。

https://github.com/tatsy/normalizing-flows-pytorch

確率的なヤコビアンの計算

def log_df_dz_unbias(g, z, n_samples=1, p=0.5, n_exact=1, is_training=True):
    """
    log determinant approximation using unbiased series length sampling
    which can be used with residual block f(x) = x + g(x)
    """

    res = 0.0
    for j in range(n_samples):
        n_power_series = n_exact + np.random.geometric(p)

        v = torch.randn_like(g)
        w = v

        sum_vj = 0.0
        for k in range(1, n_power_series + 1):
            w = torch.autograd.grad(g, z, w, create_graph=is_training, retain_graph=True)[0]
            geom_cdf = (1.0 - p)**max(0, (k - n_exact) - 1)
            tr = torch.sum(w * v, dim=1)
            sum_vj = sum_vj + (-1)**(k + 1) * (tr / (k * geom_cdf))

        res += sum_vj

    return res / n_samples

LipSwish

class LipSwish(nn.Module):
    def __init__(self):
        super(LipSwish, self).__init__()
        beta = nn.Parameter(torch.ones([1], dtype=torch.float32))
        self.register_parameter('beta', beta)

    def forward(self, x):
        return x * torch.sigmoid(self.beta * x) / 1.1

公式実装を読む方への注意

著者から提供されている公式実装では、省メモリな誤差逆伝搬の処理において、対数ヤコビアンの計算回数を減らすために、対数ヤコビアン自体の計算と、パラメータ勾配の計算に必要な計算が、どちらもノイマン級数により計算されています。

ですが、このノイマン級数を用いた計算(式\eqref{eq:neumann-series})はパラメータ勾配を考えるときだけに有効なもので、本来は対数ヤコビアンの計算に使えません。そのため、そのまま使うと分布は正しそうなものが得られますが、確率密度が高めに計算されます。これは公式実装のREADMEにも触れられていて、

By default, O(1)-memory gradients are enabled. However, the logged bits/dim during training will not be an actual estimate of bits/dim but whatever scalar was used to generate the unbiased gradients. If you want to check the actual bits/dim for training (and have sufficient GPU memory), set –neumann-grad=False. Note however that the memory cost can stochastically vary during training if this flag is False.

とあるので、ご注意ください。私の実装では、対数ヤコビアンの計算とパラメータ勾配の計算は別々に計算しているので、上記の問題はありません。

実験結果

目的の分布	再現された分布	GIF (画像をクリック)

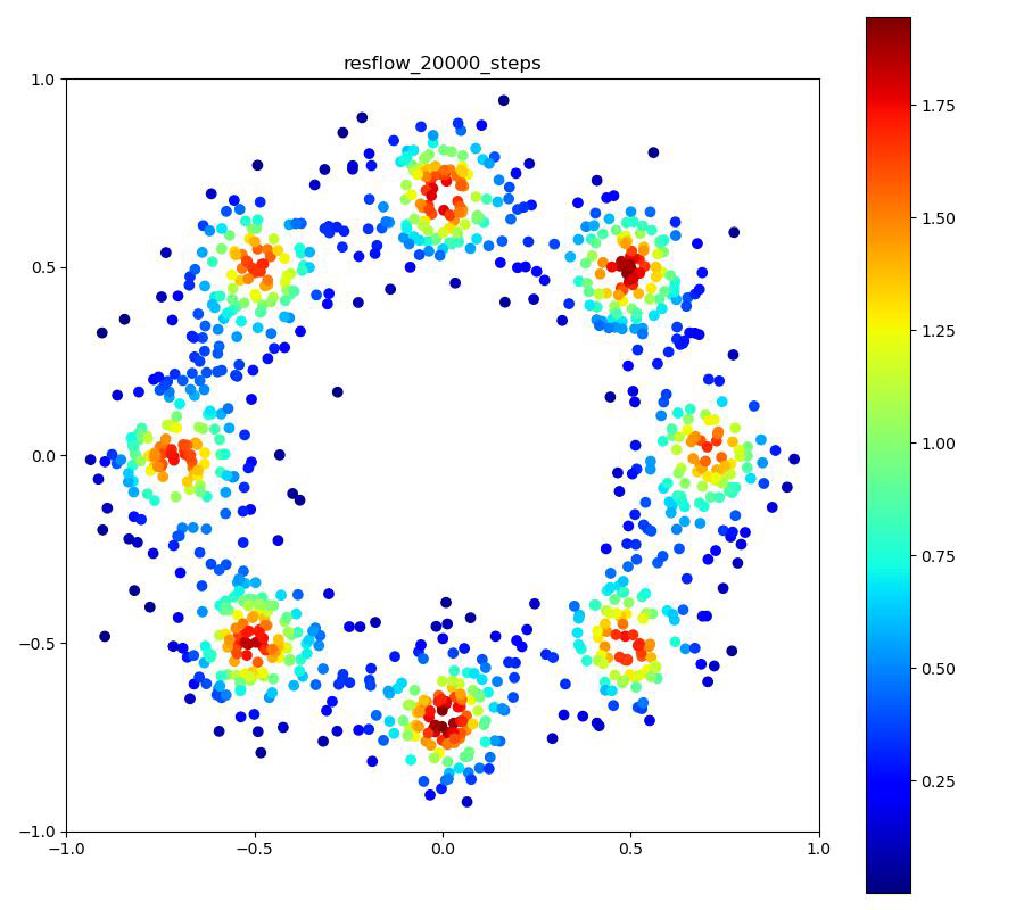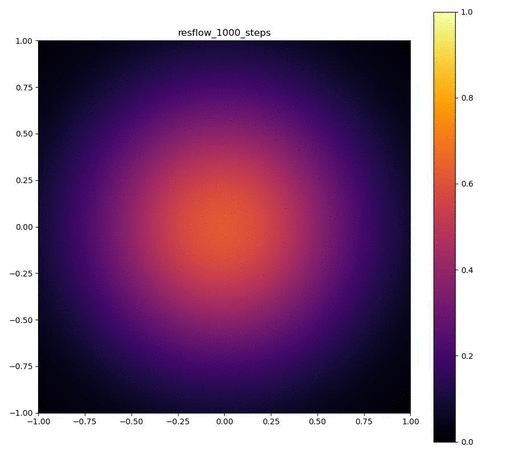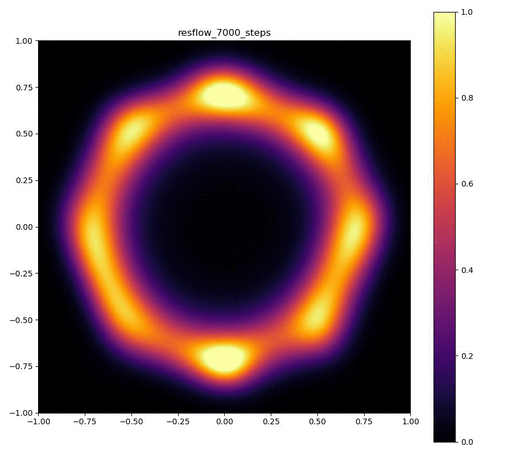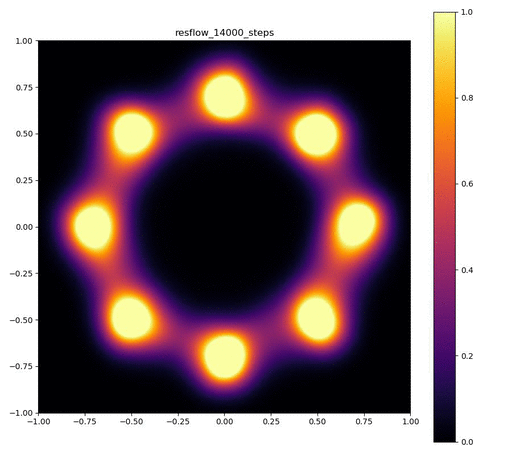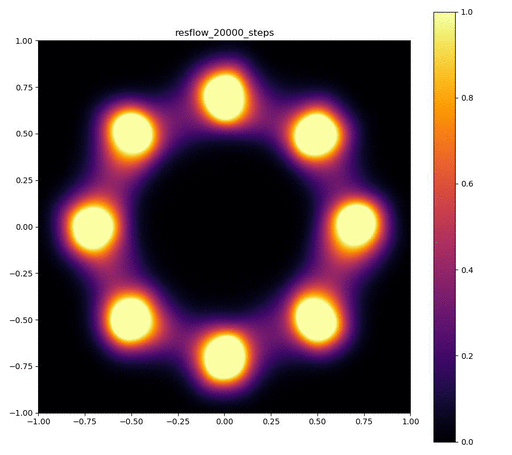まとめ

今回は可逆的な演算を可能にしたResidual NetworkであるiResNetと、それを用いてより省メモリかつ安定的なNormalizing Flowの学習を可能としたResidual Flowについて紹介いたしました。

1つ1つの内容は冒頭にも述べた通り、それほど難解な内容ではなく、落ち着いて式を追っていけば十分理解できるのですが、何分少し内容が多くなってしまいました。

次回はNormalizing Flow入門の最終回でニューラルネットを用いた常微分方程式の表現と、それに基づくNormalizing Flowの一種であるFFJORDについてご紹介したいと思います。

参考文献

[1] Behrmann et al., “Invertible Residual Networks,” ICML 2019. [arXiv]
[2] Chen et al., “Residual Flows for Invertible Generative Modeling,” NeurIPS 2019. [arXiv]
[3] Jacobsen et al., “i-RevNet: Deep Invertible Networks,” ICLR 2018. [arXiv]