Normalizing Flow入門 第7回 Neural ODEとFFJORD

こんにちはtatsyです。非常に長くなったNormalizing Flow入門も今回が最終回です。

今回はNeurIPS 2018でベストペーパーを獲得した論文であるNeural Ordinary Differential Equations (Neural ODE)[1]と、それを利用したNormalizing Flowの位置手法であるFree-form Jacobian Of Reversible Dynamics (FFJORD)[2]についてご紹介したいと思います。

Neural Ordinary Differential Equation

Neural ODEはその名前にもある通り、ニューラルネットワークと常微分方程式の共通点に着目して、ルンゲクッタ法などの数値的な常微分方程式の解法をニューラルネットの表現に用いる技術です。

突然ですが、ニューラルネットにおいて、現在はその代表的な系統の一つであるResidual Networkは

$$ \mathbf{z} = \mathbf{y} + \mathbf{g}(\mathbf{y}) $$

のように残差をニューラルネットで計算して、それを元の値に付け加えることで、値を更新していくのでした。この式は、よくよくみると、常微分方程式の数値解法に現れる式

$$ \mathbf{y}_{t+1} = \mathbf{y}_t + \frac{d\mathbf{f}(\mathbf{y})}{dt} = \mathbf{y}_t + \mathbf{f}(\mathbf{y}, t) $$

に非常によく似ています。そこでResidual Networkに現れる残差の関数$\mathbf{g}$をニューラルネットで表す代わりに、そこに時間の概念を導入し、$[0, T]$の区間で$\mathbf{f}(\mathbf{y}, t)$を積分したものが、残差となるように定式化をします。

$$ \mathbf{z} = \mathbf{y} + \int_{0}^{T} \mathbf{f}(\mathbf{y}(t), t) dt $$

このような変化の微分量を与える関数$\mathbf{f}(\mathbf{y}, t)$をニューラルネットで表そう、というのはNeural ODEのアイディアです。

ResNetの代わりにNeural ODEを用いる利点として、論文中では以下のものが挙げられています。これに関しては、思うところがあるものもあるのですが、それま「まとめ」の部分でお話ししたいと思います。

• メモリ効率が良い: ResNetを多層にする代わりに変化量の微分を表す単一のネットワークを持てば良いため、省メモリである。
• 適応的な計算: 現在のODEソルバーは許容誤差に応じて計算量を調整できるので、目的に応じてネットワーク評価にかかる時間を変えられる。
• 逆変換が計算できる: Normalizing Flowなどに必要な逆変換の計算が、時間を巻き戻す方向の積分で実現可能。
• 時間連続なモデル: Recurrent Networkは時系列データを扱うものの実際には離散的。Neural ODEは実質的にも連続的な変化を扱う。

今回の記事では、特にNormalizing Flowで用いる場合に限って話を進めていきたいと思います。

Continuous Normalizing Flow

Neural ODEの論文では、時間連続性を持つNormalizing FlowをContinuous Normalizing Flow (CNF)と呼んでおり、確率変数$\mathbf{y} = $\mathbf{z}_0$を別の確率変数$\mathbf{z} = \mathbf{z}_1$に変換する操作を次のように定義します。

$$ \mathbf{z}_1 = \mathbf{z}_0 + \int_{t_0}^{t_1} \mathbf{f}(\mathbf{z}(t), t) dt $$

これを微分形式に書き直せば、

$$ \frac{d\mathbf{z}}{dt} = \mathbf{f}(\mathbf{z}(t), t) $$

となります。繰り返しになりますが、CNFでは全時間$t$において、$\mathbf{f}(\mathbf{z}, t)$を単一のニューラルネットワークで表します。この変換の逆変換は当然ながら、

$$ \mathbf{z}_0 = \mathbf{z}_1 + \int_{t_1}^{t_0} \mathbf{f}(\mathbf{z}(t), t) dt $$

のように書けるため、順方向のみならず、逆方向についても常微分方程式の数値解法により評価できることが分かります。

対数ヤコビアンの計算

次に、CNFの対数ヤコビアンについて考えてみます。このとき、始点$\mathbf{y} = \mathbf{z}_0$に関して、$\mathbf{z} = \mathbf{z}_1$のヤコビ行列を求める必要がありますが、$\mathbf{z}_1$の中には積分式が含まれており、なおかつ被積分関数$\mathbf{f}$が$\mathbf{z}$に依存しているので、少し工夫をする必要があります。

結論を先に言うと、実際に求めたいのは対数ヤコビアンではなく、上記の変換で対数尤度がどれだけ変化するかなので、$\log p(\mathbf{z}(t))$の時間微分を求めて、これを常微分方程式の数値解法により積分することで、対数ヤコビアンに相当する部分を計算します。

ではまず、時間の変化量が微小量$\varepsilon$であるとして、

$$ \mathbf{z}(t + \varepsilon) = \mathbf{z} + \int_{t}^{t + \varepsilon} \mathbf{f}(\mathbf{z}, t) dt =: T_{\varepsilon}(\mathbf{z}(t)) $$

を考えます。ここで$T_{\varepsilon}(\mathbf{z}(t))$を$\varepsilon$についてマクローリン展開すると、

$$ \begin{equation} T_{\varepsilon}(\mathbf{z}(t)) = \mathbf{z}(t) + \varepsilon \mathbf{f}(\mathbf{z}(t), t) + \mathcal{O}(\varepsilon^2) \label{eq:trans-z-eps} \end{equation} $$

となることに注意します。

ところで、今求めたいものは対数ヤコビアンですが、この対数ヤコビアンは最尤推定の式から出てきたのでした。そこで、次はこの対数尤度に対しても、微小時間$\varepsilon$だけ微小変化させてみます。

$$ \log p(\mathbf{z}(t + \varepsilon)) = \log p(\mathbf{z}(t)) - \log \left| \det \frac{\partial T_{\varepsilon}}{\partial \mathbf{z}} \right| $$

これらを用いて$\log p(\mathbf{z})$の時間微分を求めてみると、定義に従い

$$ \frac{d \log p(\mathbf{z})}{dt} = - \lim_{\varepsilon \rightarrow +0} \frac{\log \left| \det \frac{\partial T_\varepsilon}{\partial \mathbf{z}} \right|}{\varepsilon} $$

となりますが、ここで分数部分に対してロピタルの定理を適用して、分子と分母の両方を$\varepsilon$で微分します。

$$ \begin{aligned} \frac{d \log p(\mathbf{z})}{dt} &= - \lim_{\varepsilon \rightarrow +0} \frac{\frac{d}{d \varepsilon} \log \left| \det \frac{\partial T_\varepsilon}{\partial \mathbf{z}} \right|}{\frac{d}{d \varepsilon} \varepsilon} \\ &= - \lim_{\varepsilon \rightarrow +0} \frac{\frac{d}{d \varepsilon} \left| \det \frac{\partial T_\varepsilon}{\partial \mathbf{z}} \right| }{\left| \det \frac{\partial T_\varepsilon}{\partial \mathbf{z}} \right|} \\ &= - \lim_{\varepsilon \rightarrow +0} \frac{d}{d \varepsilon} \left| \det \frac{\partial T_\varepsilon}{\partial \mathbf{z}} \right| \end{aligned} $$

式\eqref{eq:trans-z-eps}から $\varepsilon \rightarrow 0$の元では$T_{\varepsilon} \rightarrow \mathbf{I}$であることに注意してください。

一方で、ヤコビの公式という公式に従えば、行列関数の微分は

$$ \frac{d}{dt} \det \mathbf{A}(t) = \mathrm{tr} \left( \mathrm{adj}\mathbf{A}(t) \frac{d\mathbf{A}}{dt} \right) $$

のように書けます。この時$\mathrm{adj}\mathbf{A} = \det \mathbf{A} \cdot \mathbf{A}^{-1}$は行列$\mathbf{A}$の余因子行列です。この公式を用いると、上の式はさらに、

$$ \frac{d \log p(\mathbf{z})}{dt} = -\lim_{\varepsilon \rightarrow +0} \mathrm{tr} \left( \mathrm{adj} \frac{\partial T_\varepsilon}{\partial \mathbf{z}} \right) \mathrm{tr} \left( \frac{d}{d \varepsilon} \frac{\partial T_\varepsilon}{\partial \mathbf{z}} \right) = -\lim_{\varepsilon \rightarrow +0} \mathrm{tr} \left( \frac{d}{d \varepsilon} \frac{\partial T_\varepsilon}{\partial \mathbf{z}} \right) $$

とかけます。$T_{\varepsilon} \rightarrow \mathbf{I}$であったので、その余因子行列のトレースも1に収束することに注意してください。ここで、この式に式\eqref{eq:trans-z-eps}を代入すると、

$$ \begin{align} \frac{d \log p(\mathbf{z})}{dt} &= -\lim_{\varepsilon \rightarrow +0} \mathrm{tr} \left( \frac{d}{d \varepsilon} \frac{\partial T_\varepsilon}{\partial \mathbf{z}} \right) \nonumber \\ &= -\lim_{\varepsilon \rightarrow +0} \mathrm{tr} \left( \frac{d}{d \varepsilon} \frac{\partial}{\partial \mathbf{z}} \left( \mathbf{z} + \varepsilon \mathbf{f}(\mathbf{z}(t), t) + \mathcal{O}(\varepsilon^2) \right) \right) \nonumber \\ &= -\lim_{\varepsilon \rightarrow +0} \mathrm{tr} \left(\frac{\partial\mathbf{f}(\mathbf{z}(t), t)}{\partial \mathbf{z}} + \mathcal{O}(\varepsilon) \right) \nonumber \\ &= \mathrm{tr} \left(\frac{\partial\mathbf{f}(\mathbf{z}(t), t)}{\partial \mathbf{z}} \right) \label{eq:trace-estimate} \end{align} $$

以上で、対数尤度の時間微分が求まったので、これを数値積分することで対数ヤコビアンに対応する部分が求められます。

誤差逆伝搬

上記の常微分方程式による変数変換を用いた場合でも自動微分による誤差逆伝搬は可能です。ですが、一般に常微分方程式の数値解法の内部では何度も$\mathbf{f}(\mathbf{z}(t), t)$というネットワークが評価されることになり、誤差逆伝搬に必要な計算グラフが巨大になってしまう、その結果として多くのメモリを必要とするという問題があります。

この問題を解決するため、Neural ODEでは各レイヤーごとに誤差逆伝搬に必要なパラメータを求めておいて、計算グラフを保持せずに誤差逆伝搬を可能とします(この考え方はResidual Flowでも共通でした)。

誤差逆伝搬では誤差関数$\mathcal{L}$のパラメータ$\Theta$に関する勾配を求めれば良いので、最終的に求めたいものは$d\mathcal{L} / d\Theta$です。そこで、これも先ほどと同様に常微分方程式の数値解法によって求めることを目指し、これを時間$t$で微分します。合成関数と積の微分公式に従えば、

$$ \begin{align} \frac{d}{dt} \frac{d\mathcal{L}}{d\Theta} &= \frac{d}{dt} \left( \frac{d\mathbf{z}}{d\Theta} \cdot \frac{d\mathcal{L}}{d\mathbf{z}} \right) \nonumber \\ &= \frac{d\mathcal{L}}{d\mathbf{z}} \cdot \frac{d}{dt} \frac{d\mathbf{z}}{d\Theta} + \frac{d\mathbf{z}}{d\Theta} \cdot \frac{d}{dt} \frac{d\mathcal{L}}{d\mathbf{z}} \label{eq:chain-rule} \end{align} $$

となります。ここで$\mathbf{a}(t) = d\mathcal{L} / d\mathbf{z}$とおいて、$d\mathbf{a} / dt$について考えてみます。この微分については、先ほどの対数ヤコビアンの計算の時と同様に微分の定義式に従って導出していきます。¹

まず$\mathbf{a}(t)$に対して微分の連鎖公式を適用して、中間状態の$\mathbf{z}(t + \varepsilon)$での微分が現れるようにします。

$$ \mathbf{a}(t) = \frac{d{L}}{d\mathbf{z}(t)} = \frac{d{L}}{d\mathbf{z}(t + \varepsilon)} \cdot \frac{d\mathbf{z}(t + \varepsilon)}{d\mathbf{z}(t)} = \mathbf{a}(t + \varepsilon) \cdot \frac{\partial T_\varepsilon(\mathbf{z}(t))}{\partial\mathbf{z}} $$

ここで$\mathbf{a}(t)$に微分の定義式を適用すると、

$$ \begin{aligned} \frac{d\mathbf{a}}{dt} &= \lim_{\varepsilon \rightarrow +0} \frac{\mathbf{a}(t + \varepsilon) - \mathbf{a}(t)}{\varepsilon} \\ &= \lim_{\varepsilon \rightarrow +0} \frac{\mathbf{a}(t + \varepsilon) - \mathbf{a}(t + \varepsilon) \cdot \frac{\partial T_\varepsilon(\mathbf{z}(t))}{\partial\mathbf{z}}}{\varepsilon} \end{aligned} $$

となるので、ここで再び式\eqref{eq:trans-z-eps}を用いると、

$$ \begin{aligned} \frac{d\mathbf{a}}{dt} &= \lim_{\varepsilon \rightarrow +0} \frac{\mathbf{a}(t + \varepsilon) - \mathbf{a}(t + \varepsilon) \cdot \frac{\partial}{\partial\mathbf{z}} (\mathbf{z} + \varepsilon \mathbf{f}(\mathbf{z}(t), t) + \mathcal{O}(\varepsilon^2)) }{\varepsilon} \\ &= \lim_{\varepsilon \rightarrow +0} \frac{\mathbf{a}(t + \varepsilon) - \mathbf{a}(t + \varepsilon) \cdot \left( \mathbf{I} + \varepsilon \frac{\partial\mathbf{f}(\mathbf{z}(t), t)}{\partial\mathbf{z}} + \mathcal{O}(\varepsilon^2) \right)}{\varepsilon} \\ &= - \lim_{\varepsilon \rightarrow +0} \mathbf{a}(t + \varepsilon) \frac{\partial\mathbf{f}(\mathbf{z}(t), t)}{\partial\mathbf{z}} + \mathcal{O}(\varepsilon) \\ &= -\mathbf{a}(t) \frac{\partial\mathbf{f}(\mathbf{z}(t), t)}{\partial\mathbf{z}} \end{aligned} $$

という式が得られます。一方で微分順序の入れ替えを考えると、

$$ \frac{d}{dt} \frac{d\mathbf{z}}{d\Theta} = \frac{d}{d\Theta} \frac{d\mathbf{z}}{dt} = \frac{d\mathbf{f}(\mathbf{z}(t), t)}{d\Theta} $$

となるので、これらを式\eqref{eq:chain-rule}に代入します。

$$ \frac{d}{dt} \frac{d\mathcal{L}}{d\Theta} = \mathbf{a}(t) \frac{d\mathbf{f}}{d\Theta} - \mathbf{a}(t) \frac{d\mathbf{z}}{d\Theta} \frac{\partial\mathbf{f}}{\partial\mathbf{z}} $$

ここで全微分の公式

$$ \frac{d\mathbf{f}}{d\Theta} = \frac{\partial\mathbf{f}}{\partial\Theta} + \frac{\partial\mathbf{f}}{\partial\mathbf{z}} \frac{d\mathbf{z}}{d\Theta} $$

を代入すれば、

$$ \frac{d}{dt} \frac{d\mathcal{L}}{d\Theta} = \mathbf{a}(t) \frac{\partial\mathbf{f}(\mathbf{z}(t), t, \Theta)}{\partial\Theta} $$

が得られます(ここで初めて$\mathbf{f}$が$\Theta$に依存することを明示しました)。このとき$\mathbf{a}(t) = \partial{\mathcal{L}} / \partial\mathbf{z}$は誤差逆伝搬により、上位レイヤーから与えられるので、これを用いることで、そのレイヤーで必要なパラメータの勾配を求められることがわかります。

誤差逆伝搬においては、時間の終点$t_1$から積分を考えるので、積分区間の前後を入れ替えて積分すると、

$$ \frac{d\mathcal{L}}{d\Theta} = - \int_{t_1}^{t_0} \mathbf{a}(t) \frac{\partial\mathbf{f}(\mathbf{z}(t), t, \Theta)}{\partial\Theta} dt $$

という公式が得られます。このようにネットワークパラメータの勾配に関しても、常微分方程式の数値解法によって求められることが分かりました。

Free-Form Jacobian Of Reversible Dynamics (FFJORD)

Neural ODEでは、非常にエレガントな式変換により、順方向、逆方向の変数変換、ならびにヤコビアンと誤差逆伝搬の計算の全てが常微分方程式の数値解法によって与えられることが分かりました。ですが、実用的にはiResNetの時と同じように(論文の発表順序はこちらが先ですが)、一点問題が残ります。

実は、Neural ODEでは変数の時間微分を表すネットワーク$\mathbf{f}(\mathbf{z}(t), t)$が第2回で紹介したPlanar Flowになっていて、これにより式\eqref{eq:trace-estimate}の評価が簡単に行えるようにしていました。

ですが、第2回でも述べた通り、Planar Flowはそれほど表現力が高くないので、できればより一般的なネットワークを使いたいのは当然のことです。ですが、一般的なネットワークでは、トレースの計算のために愚直にヤコビ行列を評価する必要があると言うジレンマがありました。

この問題点はiResNetのそれと共通していて、iResNetではHutchinsonのトレース推定法を用いて、この問題を解決したのでした。FFJORDもiResNetと同様に式\eqref{eq:trace-estimate}の評価をHutchinsonのトレース推定法により簡略化します。

省メモリなヤコビアンの計算

この部分の議論はiResNetでの議論に比べると結構単純で、単に式\eqref{eq:trace-estimate}を以下のHutchinsonのトレース推定法の式に置き換えるだけです。

$$ \frac{d\log p(\mathbf{z})}{dt} = \mathbb{E}_{\mathbf{u} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})} \left[ \mathbf{u}^{T} \frac{\partial\mathbf{f}}{\partial\mathbf{z}} \mathbf{u} \right] $$

この式の$\mathbf{u}^{T} \frac{\partial\mathbf{f}}{\partial\mathbf{z}}$の部分は$\mathbf{u}$を逆伝搬する(torch.autograd.gradなどを使用する)ことで計算できるので、ヤコビ行列を得るために同様の計算がその行数分必要であることを考えれば、少ない計算量で近似的なトレースが得られることがわかります。

実装例

FFJORDは内部でNeural ODEを使っていますが、その部分を固定ステップ幅の数値解法(Heun法や4次ルンゲクッタ法)と適応的ステップ幅の数値解法 (Bogacki-Shampine法やDormand-Prince法)をある程度共通化して実装する部分が少し複雑です。

全体を載せるとコード量が多くなってしまいますので、詳細は以下のGitHubからご確認ください。特にflows/odeint.py, flows/cnf.pyあたりをご確認いただけると良いかと思います。

https://github.com/tatsy/normalizing-flows-pytorch

実験結果

Neural ODEのレイヤーが3層で、それぞれをDormand-Prince法により倍精度で数値積分した場合。

目的の分布	再現された分布	GIF (画像をクリック)

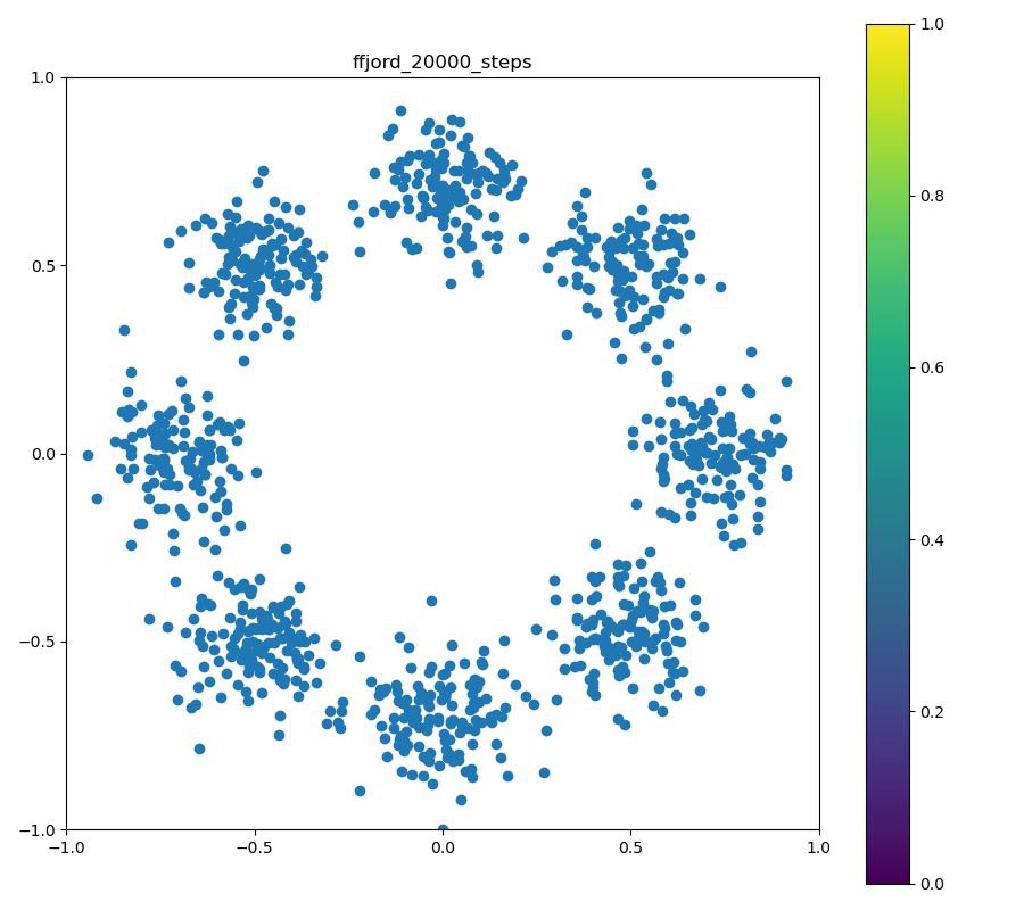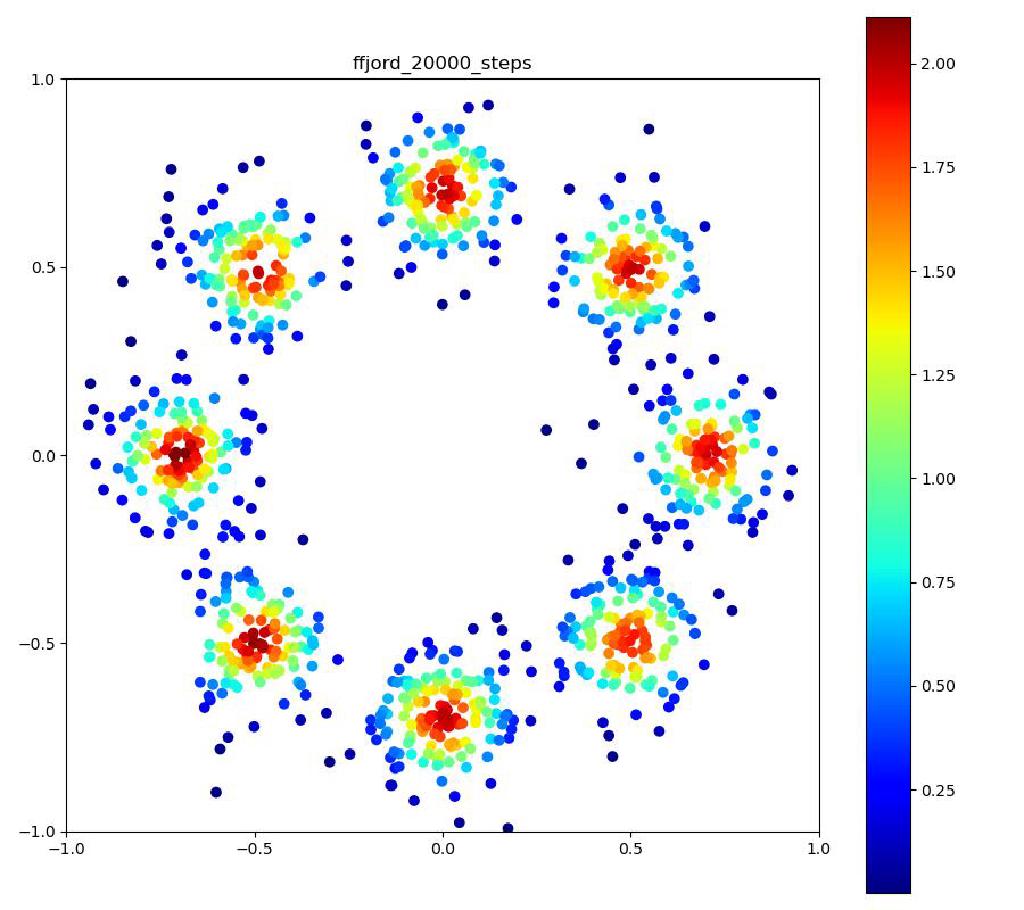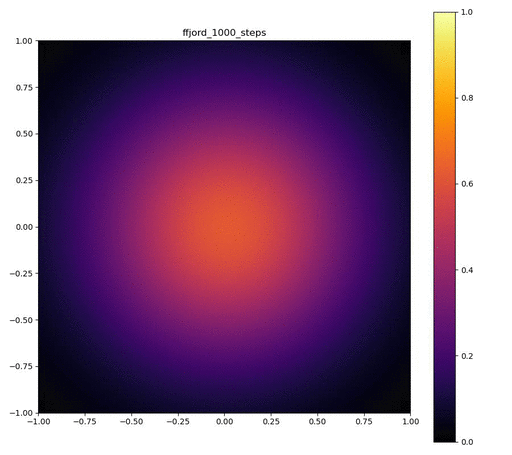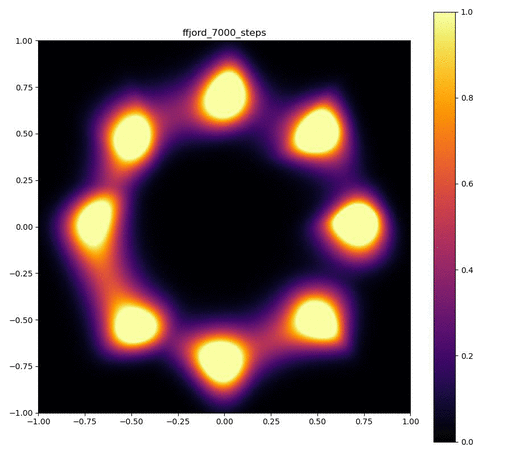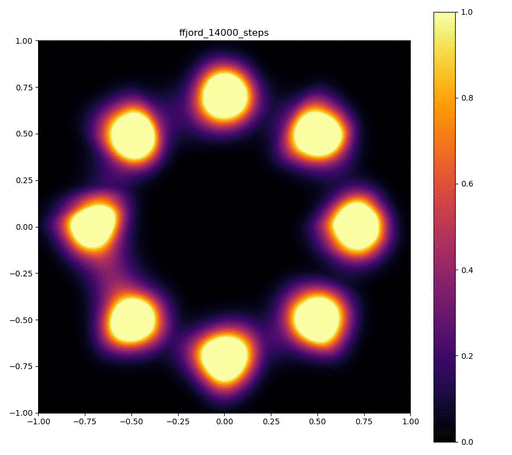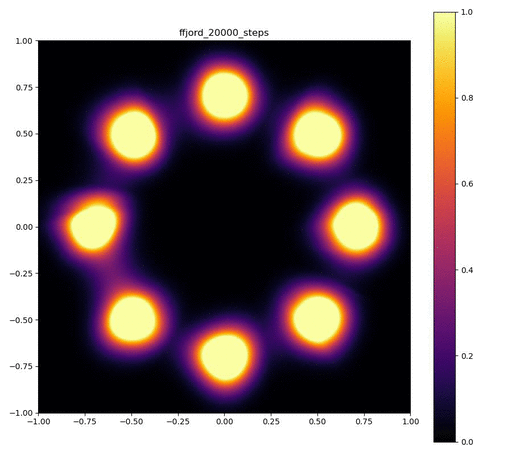まとめ

今回はNormalizing Flowの技術でニューラルネットによる常微分方程式の表現を用いたNeural ODEとFFJORDについてご紹介いたしました。

Neural ODEはNeurIPSでベストペーパーを取るくらいなので、流石に式変形などは非常にエレガントです。考え方も新しくて、とても面白いのですが、実際に自分でプログラムを書いて試してみると、実用上はまだ発展途上の技術という印象も受けました(とはいえ1, 2年で解決されるでしょう)。

まず、表現力に関してですが、ResNetを多層で積み重ねるのに比べて、単一のネットワークを使うNeural ODEの表現力が同等か？という部分に関しては、私はかなり懐疑的です。結局、表現力はパラメータ数によるところが大きいと思っていて、手法の取り扱いの簡単さなどからみても実用上はResNetの方が優先度が高いのは言うまでもないと思います。ただNormalizing Flowなどの応用では可逆性などが大事になってくるので、ケースバイケースであるとはいえそうです。

また、Neural ODEは数値解法を用いる部分がかなり不安定でオフィシャルのGitHubにも注意書きがある通り、用いる数値解放は固定のステップサイズの通常の4次精度ルンゲクッタ法などでは不十分であることが多く、実際、この実装では適応的なステップサイズを用いるDormand-Prince法が採用されています。

論文中には、この数値計算の部分にかかるネットワークの評価は70-100回程度だったと報告されていますが、そんなに評価しなければならないとしたら、素直にResNetを使った方が良い気がしてしまいます。実際、私の手元の実装でもFFJORDの訓練は他の手法と比べて、レイヤー数を減らしても数倍は遅く、実用性は低いかな、と思わざるを得ませんでした。

加えて、よくよくソースコードをみると、この数値解法の部分は倍精度で計算されていて、一般的なニューラルネットの学習で単精度が用いられていることを考えると、少しアンフェアであるような気もします(しかも単精度だと、とても不安定！)。

と、いろいろな問題は残りつつも、新しい考え方を提供した功績は大きい、ということで今回の記事を締め括りたいと思います。

Normalizing Flow入門ということで当初思っていたよりもずっと長い記事になってしまいましたが、全7回読んでくださった方も、いくつかだけつまみ食いした方も、お読みいただきありがとうございました。

参考文献

[1] Chen et al., “Neural Ordinary Differential Equations,” NeurIPS 2018. [arXiv]
[2] Grathwohl et al., “FFJORD: Free-form Continuous Dynamics for Scalable Reversible Generative Models,” ICLR 2019. [arXiv]