Programming for Beginners Programming for everyone!

k-d木による最近傍探索

k-d木の構築

k-d木は任意の次元$k$を持つ空間 ($k$-dimensionalでk-d)を分割する木構造である。k-d木は一つのノードが2つの子を持つような二分木の一種であり、一つ一つのノードは$k$次元空間内の超立方体内部に含まれる点 (あるいは別のデータ)の情報を管理する。k-d木の中では親子関係のない各ノードが支配する領域が重複することはない (親ノードは必ず子ノードの領域を支配している)。

(kd木 - Wikipediaより引用)

入力されたデータが点群である場合には、k-d木はトップダウンに作成される。ここで言う「トップダウン」というのは、最初に全ての点群を含むようなルートノードを作成し、そのルートノードを段階的に分割していくことで木を構築する操作を指す。通常、このルートノードはAABB (axis-aligned bounding box)と呼ばれる直方体によって定義される。AABBは直方体の各辺の方向がX, Y, Z軸のいずれかと平行(axis-aligned)になっているものを指す。

ノードを分割する処理はX, Y, Z軸方向のなかで、そのノードが含む「頂点位置の分散」が最大となる方向に垂直な平面で分割していく。分散の計算については、説明不要と思うが以下の通りである。

// maximum variance direction
const int count = right - left;
double muX = 0.0, muY = 0.0, muZ = 0.0;
for (int i = left; i < right; i++) {
    muX += points[i].x / count;
    muY += points[i].y / count;
    muZ += points[i].z / count;
}

double varX = 0.0, varY = 0.0, varZ = 0.0;
for (int i = left; i < right; i++) {
    varX += (points[i].x - muX) * (points[i].x - muX) / count;
    varY += (points[i].y - muY) * (points[i].y - muY) / count;
    varZ += (points[i].z - muZ) * (points[i].z - muZ) / count;
}

分割位置については、頂点を分散最大方向の変位によりソートして、その要素が半分ずつに分かれるように決定する。ある軸に沿って頂点位置をソートする操作はC++03の時代には比較演算を定義したクラスを定義する必要があったが、C++11で導入されたラムダ式を用いることで、より簡単にプログラムが描けるようになった。

// Sort
std::sort(points.begin() + left, points.begin() + right, [&](const T& p, const T& q){
    return p[maxAxis] < q[maxAxis];
});

この時、分割面は少なくとも1つの頂点を通るように選んでおき、各ノードには分割面上の情報も記録しておく。こうすることで、最近傍点を探索する時に、分割面までの距離を利用して、効率的に探索範囲を限定することができる。

以降は、この分割をノードが支配する頂点の数が1つになるまで繰り返すことでk-d木が構築される。

k-d木を用いた最近傍探索

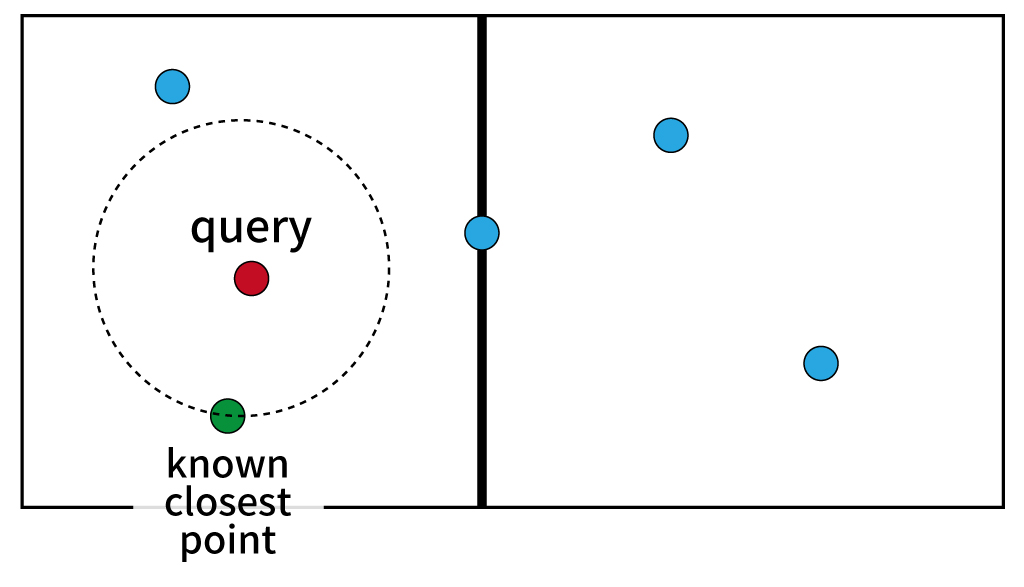
k-d木を用いると、クエリとなる頂点と最も近い頂点を効率的に探索することができる。これは、仮にクエリ頂点と今の探索しているノードとの分割面までの距離が、今見つかっている点の中で最も近いへの距離よりも遠ければ、反対側の兄弟ノードを探索する必要がなくなるためである。

例えば、上の点ではqueryと示した探索対象の点からの距離が今のところ最小の点がknown closest pointで示した緑色の点であるとする。すると、太い黒線で示した分割面は、この緑の点よりも遠くにあるため、分割面の反対側にある点は一切探索する必要がない。結果として、最近傍点の探索にかかる計算コストは入力頂点の数を$N$として、わずか$\mathcal{O}(\log N)$となる。

また、この方法を拡張すると、クエリ点からみて一定の半径内に入っている点だけを取り出したり、クエリ点から近い順に決まった数の点を取り出したりすることもできる。

テンプレート・プログラム内での実装について

k-d木の実装はなれていないとやや難しい部分もあるため、今回は最近傍点の探索と、一定の半径内に含まれる点の探索を行う関数を備えた実装をそのまま提供している。

このk-d木の実装はテンプレート・クラス (テンプレート・プログラムと言葉がややこしいが、ここでのテンプレートはC++における用語)となっていて、KDTree<Vec3>のように入力の点を表す変数の型を与えて用いる。

テンプレート・クラス (およびテンプレート関数)は、異なる型に対して、共通の機能を実装することができ、さらにテンプレート引数に与えられた型が利用条件を満たさないときにはコンパイルエラーとすることができる。

今回の実装においては、k-d木の入力点群を表す型が、T::x, T::y, T::z のように三次元座標の各要素を返し、さらに2つの点をとって、その間の距離を返す関数length(const T&, const T&)が定義されていることを仮定している。

テンプレート・プログラムで与えているVec3型はどちらの条件も満たすため、そのままKDTree<Vec3>のようにして使うことが可能である。また、頂点の番号などの追加情報をもたせたいときには、Vec3型を継承して、新しい型を定義するのが良いだろう。

クラスの継承は、初心者には難しい部分もあるので、テンプレート・プログラム内にVec3型を継承して頂点番号を加えたPoint型を定義しておいた。

// Custom struct for KD tree
struct Point : public Vec3 {
    Point() {}
    Point(const Vec3 &v, int index = -1) : Vec3(v), i(index) {}
    int i;
};

ちなみに、テンプレート関数ならびにテンプレート・クラスはとても便利な機能ではあるが、一般的にコンパイルエラーのメッセージが分かりづらくなり、また必ずヘッダファイルに定義を書かないといけないためにコンパイルにかかる時間が増える傾向にある。

意見が分かれるところではあると思うが、テンプレートを使うのは、テンプレートを使わなければ実現できないような実装をする場面 (可変長テンプレートなどを使う時)や、ベクトル型などの基本的な型を定義する場合に限定しておきたい (ちなみに後者の場合はマクロを使うことでテンプレートを使わない実装も可能、こちらはコンパイルは速いが、デバッグはより難しくなる)。

comments powered by Disqus