マーチング・キューブ法
マーチング・キューブ法は1987年にLorensenとClineによって提案されたアルゴリズムで、2020年現在、コンピュータ・グラフィクスのトップ・ジャーナルであるACM Transactions on Graphicsにおいて、最も引用されている論文である。
今日、マーチング・キューブ法とその発展形はCTやMRIなどで得られる三次元ボリュームデータを表面メッシュデータに置き換える方法として広く利用されている。
マーチング・キューブ法のアイディアは単純で、1つのキューブが持つ8つの頂点が表面メッシュの内側にあるのか、外側になるのかのすべてのパターンについて、どのようにメッシュが切られるべきなのかを表す辞書を用意する。
これらのパターンは単純には2の8乗、すなわち256通りのパターンが考えられるが、回転や鏡面対称のものをまとめると、以下の図に示すような15種類のデータとなる。
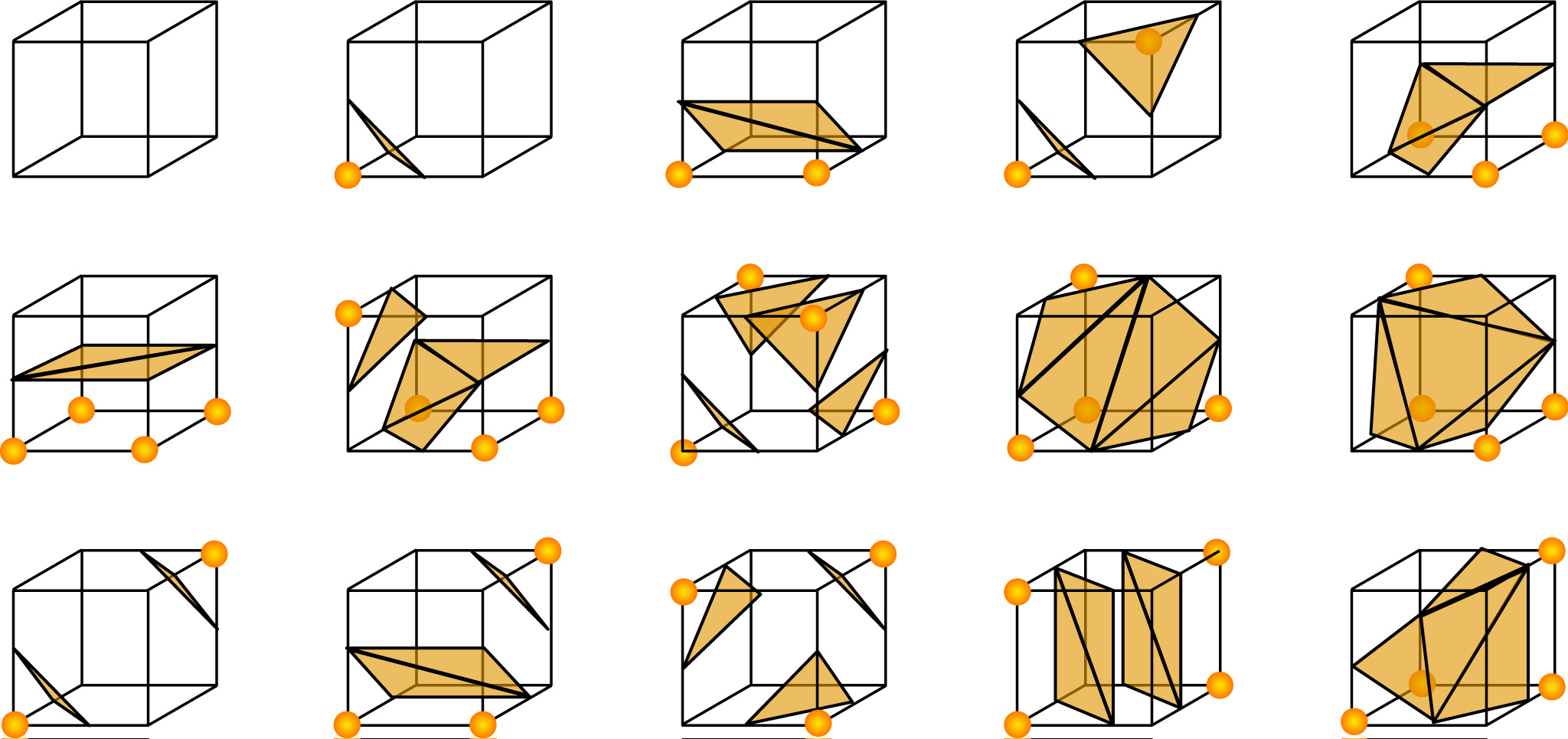
(『マーチングキューブ法 - Wikipedia』より引用)
これらの辞書の用意と、回転や考慮したメッシュへの変換は煩雑ではあるが、幸運なことに、ウェブ上に基本的な実装を含むソースコードが多数公開されている。
今回はhttp://paulbourke.net/geometry/polygonise/で公開されているコードを元に、マーチング・キューブ法を実装していく。なお、このコードはキューブの8頂点に対するインデックスの付け方に特徴があり、ビットでこれを管理しようとすると少し工夫が必要なので気をつけること (テンプレートプログラムのindexTableとウェブページ内の図を見比べてほしい)。
処理の流れ
上記のウェブページに公開されているコードではGRIDCELLが冒頭の図で言うところのキューブひとつに対応する。この構造体に対して、8つのコーナーの位置と、そのコーナーが持つボリュームの値をdoubleで格納する。
その結果をPolygonize関数に閾値 (こちらもdouble型)で渡す。すると、第3引数にある三角形 (TRIANGLE型) の配列に対して、三角形とその頂点位置を代入してくれる。何個の三角形を生成したかはPolygonize 関数の戻り値に格納される。
あとはTRIANGLE型の配列は三角形の個数分処理して、出力の頂点リストと面を構成する頂点番号リスト(テンプレートコードではそれぞれverticesとindices)に格納すれば良い。これらの手順を元にテンプレートのプログラムを埋めて、マーチング・キューブ法のプログラムを完成させよう (テンプレートプログラムは課題のページから入手できる)。
Polygonize関数の中身
上記の手順に従えば、マーチング・キューブ法の実装自体は可能だが、Polygonize 関数の中身についても見ておこう。以下の議論は自分で後述するマーチング・テトラヘドラ法を実装するときに役に立つ。
edgeTable
関数の冒頭にある edgeTable はキューブが持つ12本のエッジのうち、どのエッジ上に頂点が発生するのかを表している。
edgeTable の定義から分かる通り、この配列の長さは$2^8 = 256$であり、キューブの8つの頂点のどれが内側で、どれが外側なのかを表すビットマスクから、各エッジ上に新たな頂点が発生するのかどうかを取得できる。例えば、(0始まりで) 2番目の要素である16進数の 0x203 (最初の0xは16進数ということ)であれば、10進数で$2 \cdot 16^2 + 0 \cdot 16^1 + 3 \cdot 16^0 = 515$を表していて、これは2進数なら 0b001000000011 (最初の0b は2進数ということ)だから、1が立っているビットに相当する0, 1, 9番目のエッジ上に頂点が発生することを意味している。
2番目の要素は2が2進数表示で 0b00000010となることから、1番目の頂点だけが外側であることを表している。この場合には三角形が1つだけ発生するから、上記の考察において、3本のエッジ上に頂点が発生する事実とも一致することが分かる。
なお、前半の128個と後半の128個はキューブの頂点の内外が入れ替わったものを表しているので、新たな頂点が発生するエッジが変化することはなく、それ故edgeTableの後半は前半を逆順に並べ直したものになっている。
triTable
edgeTableの後にあるtriTableはキューブの8頂点の内外を表すビットマスクから、何番のエッジ上に発生した頂点を結んで三角形とするのかを表している。
triTableは二次元配列で、第1軸の長さはビットマスクの大きさに合わせて$2^8 = 256$となっている。一方、第2軸の大きさはマーチング・キューブ法において、1つのキューブに最大5個の三角形が発生し、それぞれが3つずつ頂点を持つことから15あれば良く、加えて、配列の終点を表すために最後の要素に-1を入れることを考慮して長さが16となっている。この時に考慮される最大の三角形5つというのは、冒頭の図に示したものよりも詳細なパターンであり、必ずしも図と一致しないことに注意してほしい。
頂点の内外ビットマスクの計算
以後の処理は、キューブの8頂点の内外を考慮したビットマスクの計算と、ビットマスクに基づいた等値面上の頂点生成、ならびに三角形として頂点を結ぶ処理になる。それほど難しいコードではないので、各自で詳細を確認してほしい。
補足: マーチング・キューブ法の拡張
マーチング・キューブ法にはいくつかの問題点が知られており、それらを解決する方法も多く提案されている。なお、CTなどのボリューム・データを扱う場合は、そもそも情報が十分に細かく、各ボクセルでマーチング・キューブを実行できるので、以下の議論を利用する場面はそれほど多くはない。
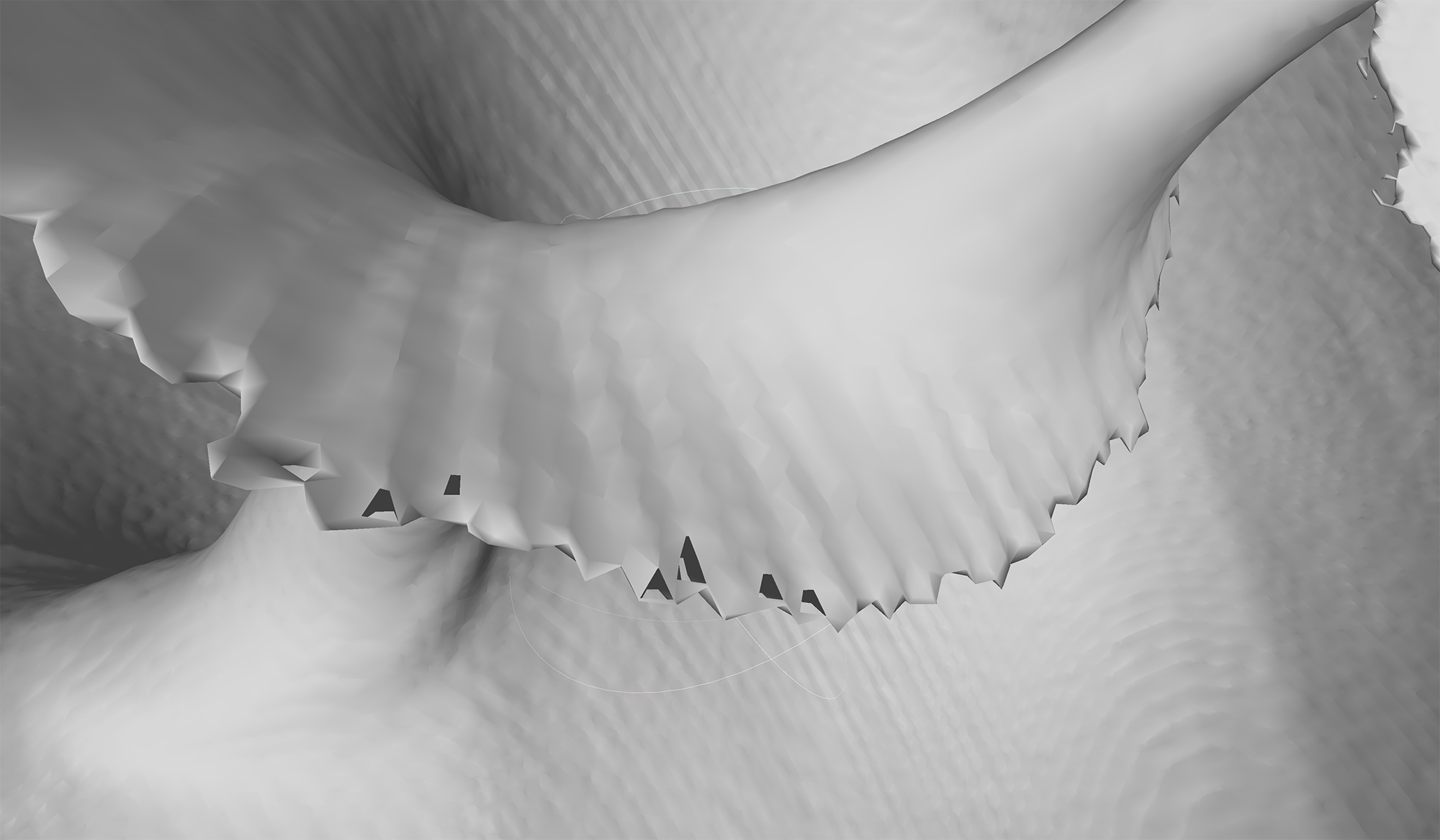
1つ目の問題は、特にキューブの取り方がメッシュの細かさに対して荒い場合に起こる問題で、隣あうキューブの間で三角形面が連続せずに穴が空いてしまう。この問題の詳細については以下の論文の図3を参考にしてほしい。
Nielsen and Hamann 1991, “The Asymptotic Decider: Resolving the Ambiguity in Marching Cubes”
http://web.cse.ohio-state.edu/~shen.94/788/Site/Reading_files/p83-nielson.pdf
上記の論文では、このような曖昧さを解決するために、曖昧となりうるパターンには複数の候補を考えておき、適宜隣のキューブが発生させた三角形ときちんと繋がるような三角形を発生させるという方法を取っている。
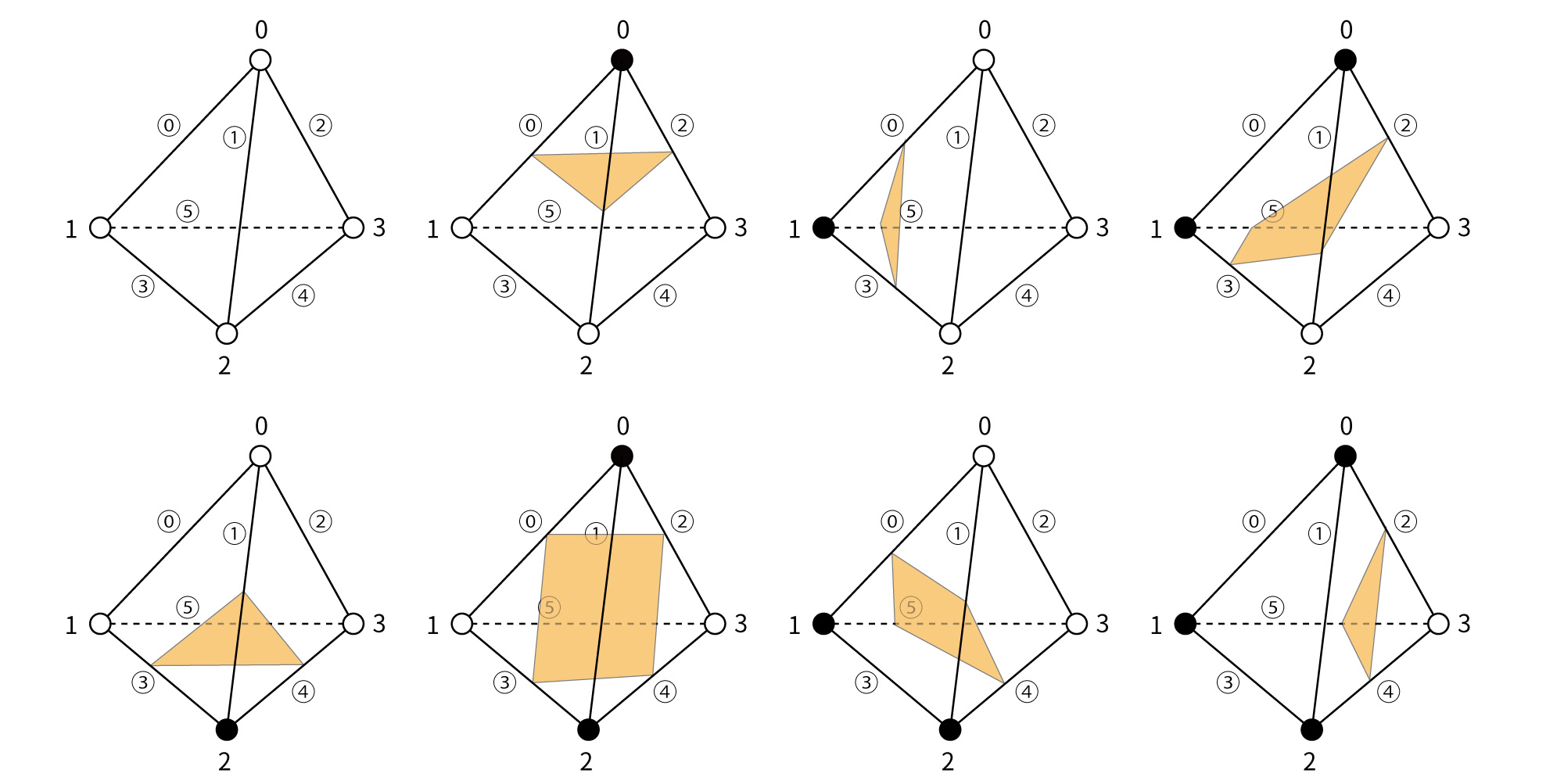
また、これとは違う考え方で、曖昧さの問題を解決した手法にMarching Tetrahedraがある。この方法は、立方体を6つの四面体に分割して、各四面体に対して面貼りのパターンを割り当てるというものである。
Treece et al. 1998, “Regularized marching tetrahedra: improved iso-surface extraction”
http://svr-www.eng.cam.ac.uk/reports/svr-ftp/treece_tr333.pdf
四面体は頂点がそもそも4つしかないため、対称性などを考慮しなくても、パターンはたったの16種類しかなく、実装の苦労が少ないのがもう一つの特徴である。以下に16例のうちの8例を示した。残りの8例はこれらの面の向きが反転したものとなる。
実際に同じデータについてマーチング・キューブ法とMarching Tetrahedraを実行した結果が以下の図である。見て分かる通り、Marching Tetrahedraではマーチング・キューブ法に見られる穴を適切に処理できている。
Marching Cubes |
Marching Tetrahedra |
2つ目の問題は、マーチング・キューブ法で細かなメッシュを再構成しようとしたときには、キューブを細かく切る以外にあまり良い方法がなく、荒いキューブでは鋭いエッジのような特徴を保持できないということである。この問題を解決するために、Extended Marching Cubesという方法が以下の論文で提案されている。
Kobbelt et al. 2001, “Feature Sensitive Surface Extraction from Volume Data”
https://www.graphics.rwth-aachen.de/media/papers/feature1.pdf
この方法ではマーチング・キューブ法同様に、同じサイズのキューブを使う。まずマーチング・キューブ法でメッシュを生成し、各頂点の法線を計算する。もし各キューブ内で発生させた頂点の法線の向きが一定以上開いていたら、feature sampleと呼ばれる余剰の点を発生させて、その点とキューブ内の頂点を結んで錐形状を作る。最後に、feature sampleを含む三角形のエッジを順に見ていき、もしエッジをフリップさせたときにfeature sampleをエッジが結ぶようになるなら、フリップ結果を保存する(論文の図9を参照)。こうすることで、キューブの数を小さく保ちながらも、鋭いエッジの情報を復元することが可能となる。
上記の問題を解決する別の方法に、以下の論文で提案されたDual Contouringもある。
Loasso et al. 2002, “Dual Contouring of Hermite Data”
https://www.cse.wustl.edu/~taoju/research/dualContour.pdf
この方法はExtended Marching Cubesのようにキューブの内部に点を発生させるのだが、通常のマーチング・キューブ法とは異なり、キューブのエッジ上には点を発生させない。その代わりに、両端点の符号が異なるエッジがある場合には、そのエッジを含む4つのキューブに発生させた点を結んだ四角形を生成する。この部分が”dual”という言葉が入っている所以である。
Dual Contouringは通常のマーチング・キューブでキューブの中に埋もれてしまう特徴を、キューブ内に1つずつ発生させる頂点の位置を調整することで保持することを試みる。Dual Contouringにおいては、各キューブのエッジ上のどの位置を面が通るかという情報があり、そのエッジ上の点における法線が求まっていると考える (このようなデータをHermiteデータという)。
キューブの内部で符号が切れ変わっているときに発生させる点の位置は、このエッジ上の頂点位置と法線の情報を使いQEM (quadric error metric)を減少させるように選ばれる。論文中の定義(式(1))から分かる通り、QEMが小さくなれば、各エッジ上の頂点における法線が、復元されるメッシュにおいても保たれるようになる。
Dual ContouringはHermiteデータに対してしか用いることができないが、マーチング・キューブのように三角形が発生するパターンを定義しておく必要がなく、実装の苦労が少なくて済む。
最後に紹介する方法はDual Marching Cubesと呼ばれる方法で、以下の論文で提案されている。
Nielsen et al. 2004, “Dual Marching Cubes: Primal Contouring of Dual Grids”
https://people.eecs.berkeley.edu/~jrs/meshpapers/SchaeferWarren.pdf
この方法は、これまでの方法のように同じサイズのキューブを使うのではなく、八分木上に定義される”dual grid”上でマーチング・キューブ法を実行する。八分木は上記のdual contouringでも用いられていたQEMが十分に小さくなるまで分割される。各八分木のノード内に発生させられた点をつないでいくと、dual gridが作られるので、各dual gridに対して通常のマーチング・キューブ法で三角形を発生させる。
こうすることで、より細かな特徴を持つ場所に、より細かな三角形が発生するようになり、データ量を大幅に削減することができる。ただし、dual gridを発生させる際に八分木上のノード同士の隣接関係を調べる必要があるため、実装は少し複雑になる。