暗号化とSSL通信

6. 暗号化とSSL通信#

インターネットが広く普及し、社会インフラとなっている現代において、サイバー空間上の 情報を悪意から守る こと（サイバーセキュリティ）は極めて重要である。

実際、インターネット上では、住所や電話番号といった個人情報や、限られた者同士の内密の対話など、機密性の高い情報が日々やりとりされており、そうした情報が部外者に漏洩し、悪用されることを防ぐために、 暗号化 をはじめとする各種のセキュリティ技術が用いられている。

本節では、暗号化の基本的知識と、現代のインターネットで広く用いられているセキュリティ技術であるSSL/TLSについて学ぶ。

6.1. 暗号化とは#

暗号化 とは、一見しても内容がわからないように、情報を符号化（変換）することである。その詳細について説明する前に、暗号化の文脈でよく用いられる用語の意味を確認しておこう。

用語	意味
平文	元々のデータ
暗号文	符号化されたデータ。特別な知識（鍵）を持たない者には読めない
暗号化	平文を暗号文へと変換すること
復号	暗号文を平文へと変換すること（復号化ではない）
鍵	暗号化や復号において必要となる「特別な知識」
暗号方式 (暗号アルゴリズム)	暗号化/復号の方法
暗号解読	鍵を使わずに暗号文から平文を得ること

以下で説明する暗号のアルゴリズムを理解するうえでは、各暗号の鍵が何であって、鍵を用いたどのような処理により 暗号化 と復号がなされるのかを理解することが重要である。

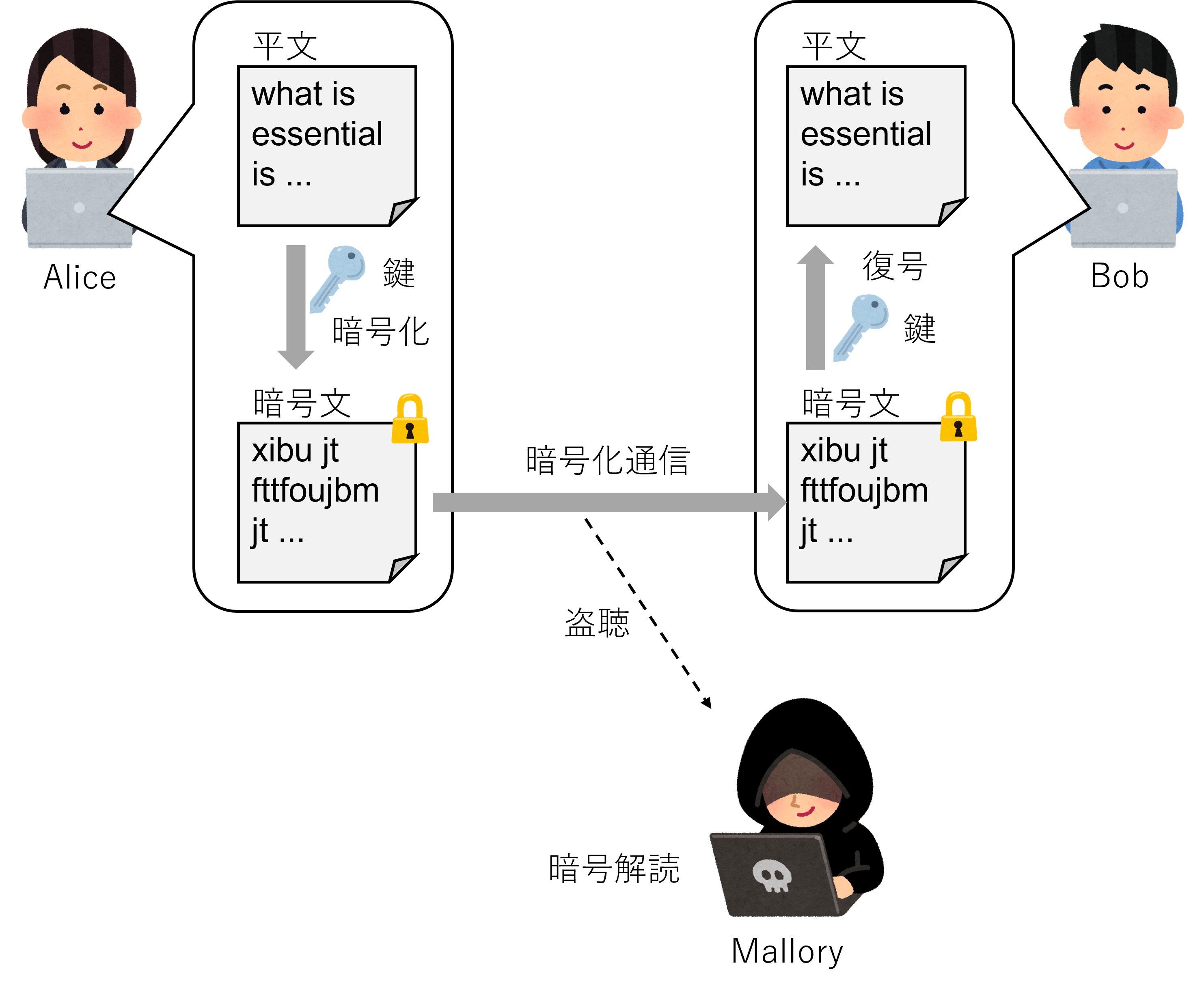
Tip

セキュリティ分野の技術説明では、しばしば以下のような架空の人物名が用いられる。

Alice
Bob
Carol
Dave

悪意ある攻撃者 (malicious attacker) としては

Mallory
Marvin

などが用いられる。

シーザー暗号#

古典的な暗号方式として、 シーザー暗号 がある。Iulius Caesar (紀元前100年-紀元前44年) が使ったと言われる 換字式暗号 の一種である。

原理は単純であり、平文の各文字を $k$ 文字シフトさせる。仮に、平文を構成する文字集合をアルファベット小文字26文字とすると、$k=3$の場合に、aはdに、bはeに置き換える。また、xはaに、yはbに、zはc というようにアルファベットの最後まで到達した場合には最初に戻って置き換える (循環シフト)。

表 6.1 シーザー暗号の例 ($k=3$)#
	1	2	3	4	5
平文	h	a	p	p	y
暗号文	k	d	s	s	b

ここでは簡単のためにアルファベット小文字26文字としているが、順序が決まってさえいれば、どのような文字集合でも同様の暗号化が可能である。

シーザー暗号においては、

鍵: 整数 $k$
暗号化: $k$ 字シフト
復号: $k$ 字逆シフト

である。

シーザー暗号をプログラムで実現するにあたり、平文 m の各文字を k だけシフトする関数 shift(k, m) を考える。この関数が定義されているとすれば、シーザー暗号のプログラムは以下のようになるだろう。

"""
caesar.py: シーザー暗号の実装例
"""


def shift(k, m):
    """mの各文字をkだけシフトした文字列を返す"""
    # !!! 各自で実装する !!!
    pass


def enc(k, m):
    return shift(k, m)


def dec(k, m):
    return shift(-k, m)


# # 以下、動作確認用コード
# if __name__ == '__main__':
#     k = int(input('Input key (integer): '))
#     plain_text = input('Input plain text: ')
#     encrypted_text = enc(k, plain_text)
#     print('Encrypted text:', encrypted_text)
#     print('Decrypted text:', dec(k, encrypted_text))

ここまでを踏まえて、シーザー暗号を実現するプログラムを作成する以下の練習問題に取り組んでみよう。

練習問題1

上記のプログラムの shift(k, m) を完成させよ。

暗号解読#

与えられた暗号文から、鍵を用いずに平文を得ることを 暗号解読 という。

古典的な暗号解読手法として、 総当たり攻撃（brute-force attack） がある。存在し得るすべての鍵を試すという力任せな方法であるが、鍵空間が小さい場合には有効である。

例えば、文字集合がアルファベット小文字26文字のシーザー暗号であれば、$k$ はわずか26通りしかない。従って、ある程度長い暗号文が得られれば、プログラムを用いて全パターンの $k$ で復号を行い、意味のある文章が得られる本当の$k$を簡単に発見できる。

一方、鍵空間が大きい場合には、総当たり攻撃は時間がかかりすぎて非現実的となる。一例として、後述する暗号方式AESの鍵は128bit, 192bit, 256bitのいずれかの長さを持つビット列であり、最も脆弱な128bitの場合であっても、存在し得る鍵は $2^{128}$ という膨大な数になる。なお、 $2^{128}$ は、おおむね340兆の1兆倍の1兆倍である。

練習問題2

簡単な計算を一定回数繰り返すプログラムを作成し、膨大な回数のループ (少なくとも100万程度)にどのくらい時間がかかるかを測定してみよう。一例としてフィボナッチ数を1000で割った剰余を求める計算を非常に大きな自然数 $N$ まで繰り返したらどうなるだろうか？

時間の計測にはPythonの time モジュールを使えば良い (使用方法については各自で調べること)。得られた結果から推定すると、$2^{128}$回のループにはどの程度の時間がかかるだろうか。

暗号文が十分に長い場合は、文字の出現頻度を見ることで、総当たりよりも効率的に解読することができる。

これを 頻度分析 という。

以下に、与えられたテキストについて、アルファベット小文字の出現頻度を集計する関数の例を示す。

def freq(text):
    freqs = [0] * 26
    for c in text:
        if ord('a') <= ord(c) <= ord('z'):
            index = ord(c) - ord('a')
            freqs[index] += 1

    return freqs

以下のグラフは、上記関数を用いて、シャーロック・ホームズシリーズの短編『ボヘミアの醜聞』冒頭1パラグラフの頻度を調べたものである。

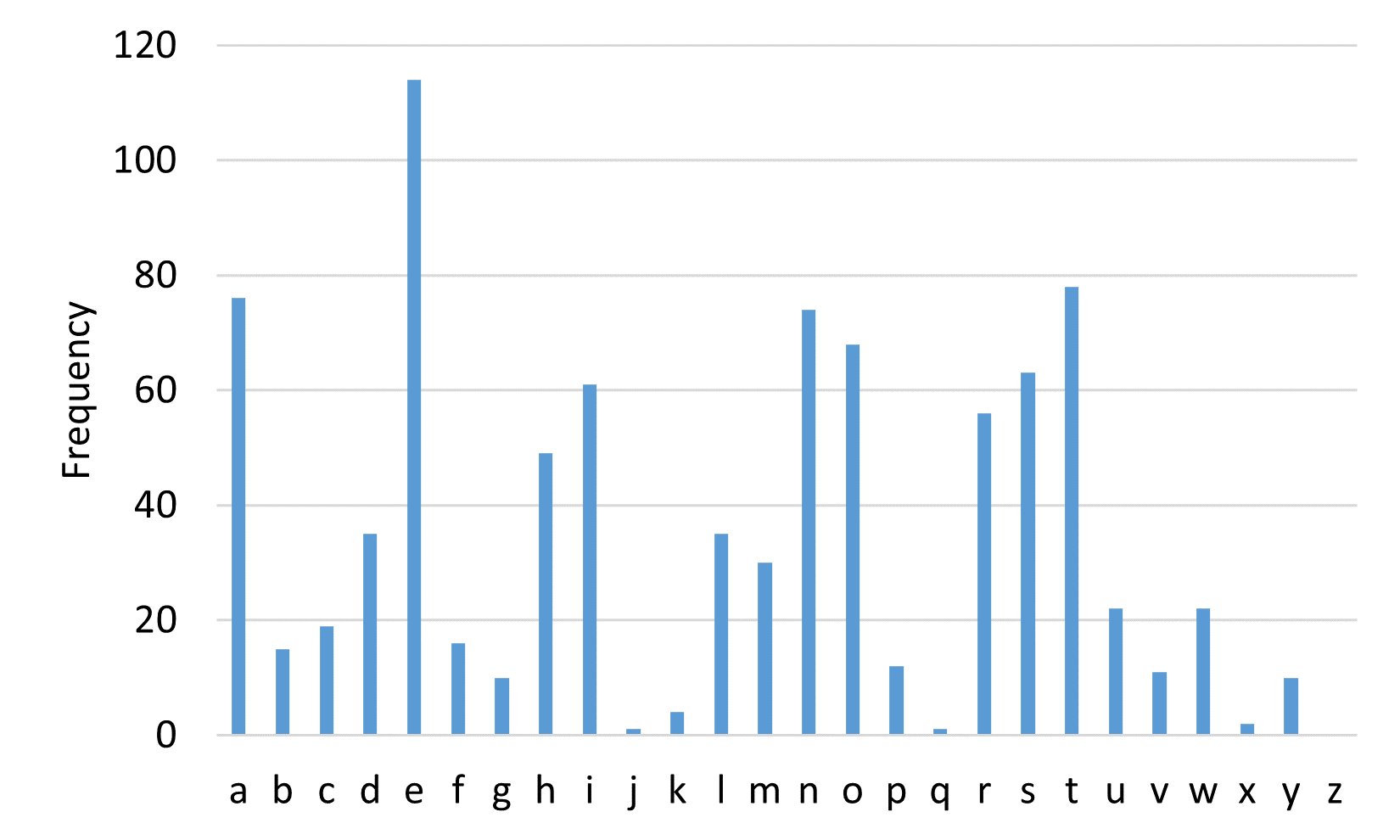
このように、英文であれば一般に a, e, t の出現頻度が高く、j, q, x, z の出現頻度が低い。多くの場合 e が最多となるため、暗号文の最多出現文字と e の間のオフセットを計算すれば、その値が鍵であることが推測できる。

練習問題3

上記の freq 関数を用いて、頻度分析をおこなう関数の例を以下に示す。

k = に続く箇所は意図的に削除してある。適切な内容で埋めて、関数を完成させよう。（もちろん、穴埋めでなく、全体を作り直しても良い）

import numpy as np


def freq_analysis(text):
    freqs = freq(text)
    max_index = np.argmax(freqs)
    # k = ???

    return dec(k, text)

完成したら、任意の英文テキストを暗号化し、鍵 $k$ を使わずに復号できるか試してみよう。短文ではうまくいかないので注意。

6.2. 暗号方式の種類#

言葉を用いてコミュニケーションをとる人類にとって、情報を一部の限られた相手に伝える（それ以外の相手には秘匿する）方法には、古来、高い需要があった。代表的な暗号方式を下表に示す (表の登場年代はおおまかな時期を表しており、厳密ではないことに注意)。

表 6.2 代表的な暗号方式#
登場年代	暗号方式	種別
紀元前600年頃	スキュタレー暗号	共通鍵暗号方式
紀元前100年頃	シーザー暗号	共通鍵暗号方式
1550年頃	ヴィジュネル暗号	共通鍵暗号方式
1920年頃	エニグマ暗号	共通鍵暗号方式
1976年頃	DES	共通鍵暗号方式
1976年頃	Diffie-Hellman鍵共有法	公開鍵暗号方式
1977年頃	RSA暗号	公開鍵暗号方式
2000年頃	AES	共通鍵暗号方式

表にあるように、暗号方式には大きく 共通鍵暗号方式 と 公開鍵暗号方式 がある。

共通鍵暗号方式 とは、前述のシーザー暗号の例のように、暗号化と復号において同じ鍵（共通鍵）を用いる暗号方式である。現代において最も広く用いられている共通鍵暗号方式は AES (Advanced Encryption Standard) であろう。無線LANルータの設定画面等で、AESという単語を目にしたことがある人もいるかもしれない。

しかし、共通鍵暗号方式を用いる場合、鍵を共有する方法が問題となる。鍵を暗号化すれば安全に送ることができるが、暗号化するためには鍵の共有が必要という、鶏卵問題に陥ってしまうのである。暗号化せず、平文で鍵を安全に送るためには、（物理的に）金庫に入れて輸送するといった手間とコストのかかる方法が必要となる。

一方で、 公開鍵暗号方式 とは、暗号化と復号において異なる鍵を用いる暗号方式である。暗号化に用いる鍵を 公開鍵 、復号に用いる鍵を 秘密鍵 と呼ぶ。公開鍵は文字通り広く公開し、秘密鍵は復号する者以外には渡らないよう厳重に保管される。

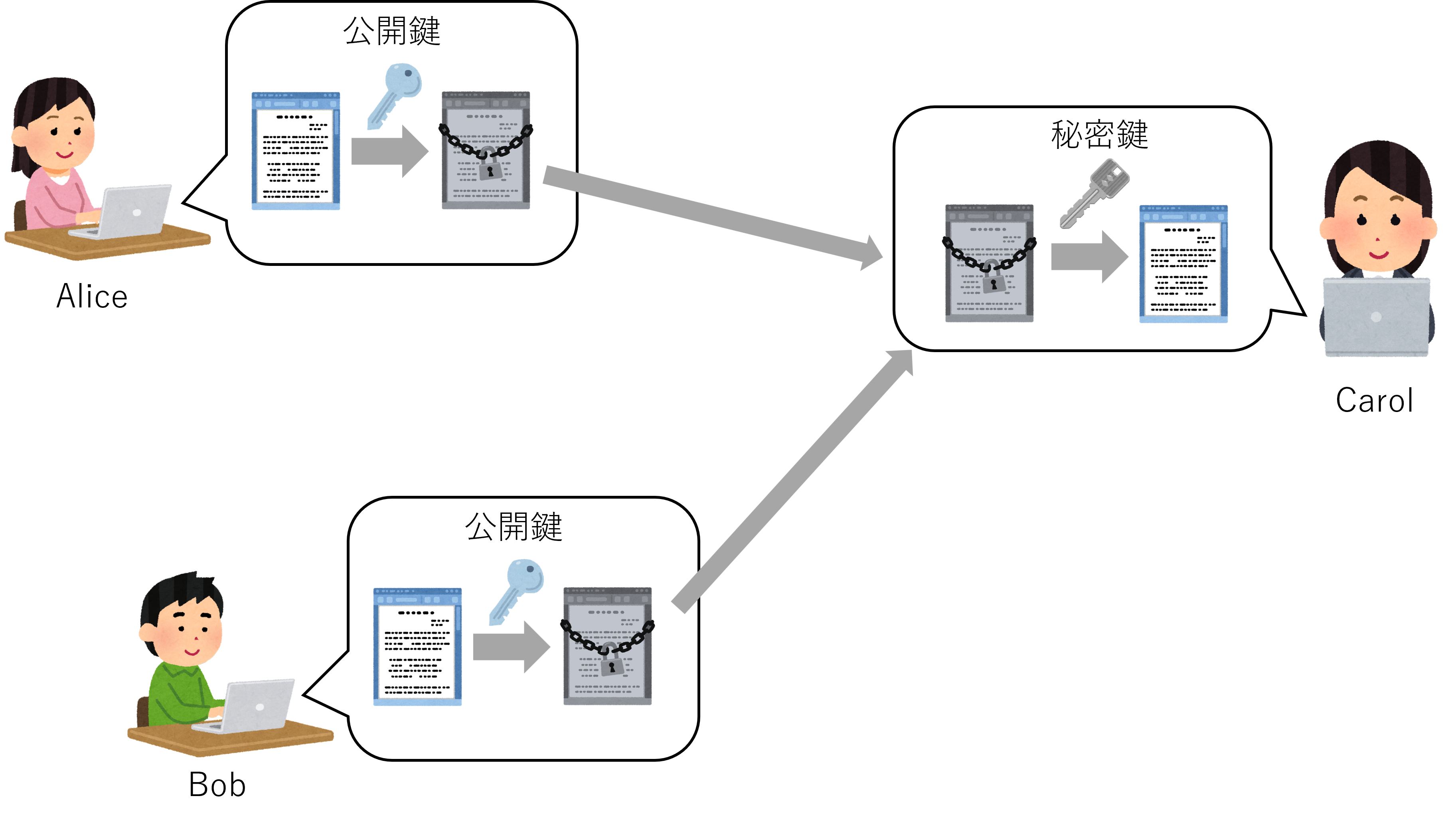
../../_images/public_key_cryptography.png — 図 6.1 公開鍵暗号方式の概念図#

図 6.1 の例では、暗号文を受け取るCarolが公開鍵と秘密鍵を用意し、前者を公開する。 Carolに情報を送りたいAliceとBobは、それぞれ、公開鍵を用いて暗号化する。 AliceがCarolへ送る暗号文は、秘密鍵を持たない者、たとえばBobには復号ができない。このように、同じ公開鍵を使っていても、 秘密鍵が無い限りは復号ができない ので、公開鍵は誰に知られても問題が無く、広く公開することができる。

例えば、初めて利用するオンラインショップであっても、鍵を事前に郵送でやりとりするようなことは必要なく、そのショップの公開鍵を用いることで、暗号通信による安全な買い物をすることができる。新たな相手と素早く安全な通信を開始することが可能となったという点において、公開鍵暗号方式はインターネット産業の発展に多大な寄与をした技術であると言える。

公開鍵暗号方式は処理負荷が大きいため、しばしば、共通鍵暗号方式と組み合わせて用いられる（ ハイブリッド暗号 ）。

すなわち、通信開始時は公開鍵暗号方式を用いて共通鍵の共有を（安全に）行い、それ以降は共通鍵暗号方式によって通信を行う。後述する SSL/TLS においても、ハイブリッド暗号が採用されている。

6.3. RSA暗号#

非常に広く用いられている公開鍵暗号方式のひとつとして、 RSA暗号 が挙げられる。 RSAは開発者3名のファミリーネームの頭文字である（Ron Rivest, Adi Shamir, Leonard Adleman）。

RSA暗号は、巨大な整数の 素因数分解が極めて計算困難であることに基づく 暗号方式である。この際、RSA暗号で暗号化されるのは、文章のようなものではなく、数値データであることに注意してほしい。

従って、平文が文章である場合には、共通鍵暗号を用いて暗号化したあとで、暗号化に用いた共通鍵の情報を公開鍵暗号で暗号化するのである。例えば、AESを用いて文章を暗号化する場合には、128ビットや256ビットなどのランダムなビット列を鍵として用いるが、このビット列を整数とみなして、これをRSA暗号で暗号化するのである。

そのため、以下の説明では、 平文、暗号文ともに整数である ことに注意してほしい。

RSA暗号による暗号化と復号は、平文を $T_p \in \mathbb{N}$、暗号文を$T_e \in \mathbb{N}$とすると次の式で表すことができる。

\[\begin{split} \begin{align} T_e \equiv T_p^E \pmod N \\ T_p \equiv T_e^D \pmod N \end{align} \end{split}\]

すなわち、

平文 $T_p$ を $E$ 乗して $N$ による剰余をとったものが暗号文 $T_e$
暗号文 $T_e$ を $D$ 乗して $N$ による剰余をとったものが平文 $T_p$

である。この際、暗号化に用いられる鍵は $(E, N)$ という整数のペアであり、復号に用いられる鍵は $(D, N)$ という整数のペアである。

従って、RSA暗号においては、

公開鍵: $(E, N)$
秘密鍵: $(D, N)$

となる。この際、上記の関係性を満たすような都合の良い $E$, $D$, $N$ をどのように決めるのかが問題になる。

以下では、$N$, $E$, $D$ の順で、どのように整数を決定するかを見ていこう。

Nの計算#

RSA暗号は、巨大な整数の素因数分解が極めて計算困難であることに基づくと述べた。この原理に基づき、整数 $N$ は2つの大きな素数 $p$, $q$ の積として

\[ N = p \times q \]

で定義される。

この際、$p, q$は小さすぎると容易に暗号解読できてしまい、大きすぎると処理負荷が大きくなってしまう。現在広く用いられているRSA-2048（鍵長2048bitのRSA暗号）の場合、素数$p$, $q$には1024bitの整数を用いる。

素数の生成は、疑似乱数生成器を用いて乱数を作り、その数が素数であるか否かを判定することで行われる。素数判定には、Miller–RabinテストやFermatテストといった素数判定のアルゴリズムが用いられる。

Eの計算#

2つの整数 $a$, $b$の最小公倍数を $\text{lcm}(a, b)$、最大公約数を$\text{gcd}(a, b)$ で表す。前述の素数$p$, $q$に対し、$L = \text{lcm}(p-1, q-1)$とすると、$E$は以下の条件を満たす必要がある。

$1 < E < L$
$\text{gcd}(E, L) = 1$　($E$ と $L$は互いに素)

これらの条件を満たす $E$ は、一例として以下の手順で発見することができる。

疑似乱数生成器を用いて、$1 < E < L$ を満たす整数をひとつ選ぶ
作成した整数が $\text{gcd}(E, L) = 1$ を満たすかどうか確認
$\text{gcd}(E, L) \neq 1$ の場合には、1に戻る

Dの計算#

$D$の計算でも、$E$の計算に用いた $L = \text{lcm}(p-1, q-1)$ を用いる。$D$は以下の条件を満たす必要がある。

$1 < D < L$
$E \times D \equiv 1 \pmod L$

この条件を満たす $D$ も、単純には、次の手順で発見することができる。

疑似乱数生成器を用いて、$1 < D < L$ を満たす整数をひとつ選ぶ
作成した整数が $E \times D \equiv 1 \pmod L$ を満たすかどうか確認
$E \times D \not\equiv 1 \pmod L$ の場合には、1に戻る

鍵生成の例#

$E, D, N$の計算について、具体例を考えてみよう。ここでは、2つの素数として $p = 11$、$q = 13$ を用いる。

import math

p = 11
q = 13
N = p * q
L = math.lcm(p - 1, q - 1)

print(f'N = {N}, L = {L}')

N = 143, L = 60

ここで、 $1 < E < L$ を満たし、かつ $\text{gcd}(E, L) = 1$ となる $E$ を探す。

import numpy as np

# シードを固定しておく
np.random.seed(123)

while True:
    E = np.random.randint(2, L)
    if math.gcd(E, L) == 1:
        break

print(f'E = {E}')

E = 47

このようにして求められた $E$ を用いて、 $1 < D < L$ を満たし、かつ $E \times D \equiv 1 \pmod L$ となる $D$ を探す。

# シードを再度固定
np.random.seed(456)

while True:
    D = np.random.randint(2, L)
    if (E * D) % L == 1:
        break

print(f'D = {D}')

D = 23

このようにして公開鍵 $(E, N)$ と秘密鍵 $(D, N)$ が得られたら、平文を $T_p = 115$ として暗号化と復号を試してみよう。

# 暗号化
T_p = 115

# (T_e ** E) はオーバーフローする可能性があるので、逐次的に計算
T_e = 1
for i in range(E):
    T_e = (T_e * T_p) % N

print(f'Encrypted T_e = {T_e}')

Encrypted T_e = 58

# 復号
T_d = 1
for i in range(D):
    T_d = (T_d * T_e) % N

print(f'Decrypted T_d = {T_d}')

Decrypted T_d = 115

この結果から分かる通り、前述のアルゴリズムにより、RSA暗号に必要な $E$, $D$, $N$ を計算と、暗号化と復号を行うことができた。

RSA暗号の解読#

前述の手順により、鍵ペアの生成および暗号化・復号が行えるわけであるが、この手法は果たして本当に安全なのだろうか。すなわち、攻撃者によって暗号が解読されてしまうことはないのであろうか。

攻撃者が知り得る情報は、$T_e, E, N$である。$E, N$は公開鍵なので、攻撃者も入手できる。 $D$ を総当たり攻撃で見つけることは、現実的ではない。なぜなら、$D$ は2048bit等の十分に大きな桁数をとることが一般的であり、探索空間が膨大すぎるためである。

別のアプローチとして、もし$N$から素数$p, q$を求めることができれば、$D$を算出して暗号解読することができそうである。 $N$から素数$p, q$を求めるとは、すなわち$N$の 素因数分解 である。しかしながら、現在のところ、大きな整数の素因数分解は困難であるとされており、高速な計算方法は見つかっていない。この、素因数分解の困難性がRSA暗号の安全性のひとつの根拠となっている。

言葉を変えると、仮に高速な素因数分解を可能とする手法が発明されれば、RSA暗号の安全性は失われることとなる。実際、量子コンピュータを用いたShorのアルゴリズムは、大きな整数の素因数分解を高速に実現できることが知られている。現状、実際の量子コンピュータでは、RSA-2048に用いられるほどの巨大な整数を扱うための量子ビット数や精度は確保できていないが、将来的に量子コンピュータの性能が向上すれば、RSA暗号の安全性は失われる可能性がある。このように技術の進歩によって安全性が失われることを 危殆化 という。

補足: より大きな整数を扱う方法#

上記の例では $p$ と $q$ の例として非常に小さな素数を用いたが、例えば、RSA-2048で用いられる素数は1024ビットの大きさを持つ非常に巨大な整数である。

そのため、前述のように適当な整数を選んで $\text{gcd}(E, L) = 1$ となることを確認するような力任せ探索では、現実的な時間内に鍵を生成することができない。

より大きな整数を扱うためには $E$ や $D$ の計算において、より効率的なアルゴリズムが必要になる。

高速版 Eの計算#

2つの整数 $N$ と $L$ が与えられた場合に $E$ が満たすべき条件は次の2つであった。

$1 < E < L$
$\text{gcd}(E, L) = 1$

しかし、$L$ が非常に大きな整数であることを考えると、 $L$ と互いに素な $E$ を見つけることは (その候補が非常に多いと言っても) それなりに時間がかかるものである。

そのため、一般的なRSA暗号の実装では、 $E$ にある程度の大きさの素数を用いることが多い。例えば、$E = 65537$ ($2^{16}$ + 1) はよく用いられる値である。

このように $E$ の選択肢を絞ったうえで、 $p$ と $q$ の2つの素数が $E$ と互いに素になる $L$ を作るように生成するのである。この時、 $L$ が $p - 1$ と $q - 1$ の最小公倍数であることを考慮すると、固定の $E$ に対して、$p-1$ と $q-1$ がいずれも $E$ と互いに素な関係となれば良い。

高速版 Dの計算#

2つの整数 $E$ と $L$ が与えられた場合に $D$ が満たすべき条件は次の2つであった。

$1 < D < L$
$E \times D \equiv 1 \pmod L$

実は、この2つ目の条件を満たすような $D$ は $L$ を法とする割り算を考えれば求めることができる。

今、仮に modを考えないとするなら、 $E \times D = 1$ となる $D$ は当然 $D = 1 / E$ である。これをもう少し噛み砕くと、方程式の両辺に $E$ の逆数、もう少し厳密に言うと逆元を掛けているのである。

実は、剰余を求める計算は一種の群構造をなしており、逆元の概念が存在する。もともと、とある元 $a$ に対する逆元というのは、単位元 $e$ に対して、 $a \times b = e$ を満たすような $b$ のことである。

これを剰余を求める計算に当てはめると、$E \times D \equiv 1 \pmod L$ における単位元は $1$ であるから、 $D$ は $E$ の逆元であると言える。

このような剰余における逆元は 拡張ユークリッドの互除法 というアルゴリズムで効率的に求めることができる。

拡張ユークリッドの互除法#

拡張ユークリッドの互除法 は、2つの自然数$a, b$について、

(6.1)#\[ ax + by = \text{gcd}(a, b) \]

となる整数 $x$, $y$ の組を求める手法である。この手法は、その名前の通り $a$ と $b$ の最大公約数 $\text{gcd}(a, b)$ を求める ユークリッドの互除法 を基にした手法である。

拡張版について説明する前に、まずユークリッドの互除法について簡単に説明する。今、2つの整数 $a_0$, $b_0$ の最大公約数を求めたいとしよう。ユークリッドの互助法では、$a_i$ と $b_i$ を次のように更新する。

\[\begin{split} a_i = b_{i - 1} \\ b_i = a_{i - 1} \mod b_{i - 1} \end{split}\]

この計算を $b_i = 0$ となるまで繰り返すと、その時に得られた $a_i = b_{i - 1}$ が $a_0$ と $b_0$ の最大公約数 $\text{gcd}(a_0, b_0)$ となる。

このアルゴリズムは最大公約数について

(6.2)#\[ \text{gcd}(a, b) = \text{gcd}(a - mb, b) \]

が $a - mb > 0$ となる整数 $m$ に対して成り立つことを根拠にしている。

ユークリッドの互除法の簡単な証明

$a$ と $b$ の最大公約数を $c = \text{gcd}(a, b)$ とする。また、$a' = a - mb$ とする。

このとき、$a = p c$, $b = qc$ のように表せる ($p$, $q$ は互いに素な整数)。従って、$a - mb = (p - mq)c$ であることから、少なくとも、$\text{gcd}(a', b)$ は $c$ の倍数であることが分かる ($p - mq$ と $q$ に公約数があるかもしれないから)。

反対に、$c' = \text{gcd}(a', b)$とすると、$a' = p' c'$, $b = q' c'$ のように表せる ($p'$, $q'$ は互いに素な整数)。従って、$a = a' + mb = (p' + mq')c'$ であることから、少なくとも、$c = \text{gcd}(a, b)$ は $c'$ の倍数であることが分かる。

以上より、$c$ は $c'$ の倍数で、かつ$c'$ は $c$ の倍数であるが、これが成り立つのは $c = c'$ の場合のみである。故に $\text{gcd}(a, b) = \text{gcd}(a - mb, b)$ が成り立つ。

では、ここまでの議論を踏まえて、拡張ユークリッドの互除法について見ていこう。上記の議論と同様にして、$a = a_0$, $b = b_0$ とし、次の方程式を考える。

\[ a_0 x_0 + b_0 y_0 = \text{gcd}(a_0, b_0) \]

この式は、(6.2) を用いると、 $a_0$ を $b_0$ で割った時の商を $m_0$ として、次のように書き直せる。

\[ (a_0 - m_0 b_0) x_0 + b_0 (y_0 + m_0 x_0) = \text{gcd}(a_0 - m_0 b_0, b_0) \]

ここで、$a_1 = b_0$, $b_1 = a_0 \mod b_0$、$x_1 = y_0 + m_0 x_0$、$y_1 = x_0$ とおくと、

\[ a_1 x_1 + b_1 y_1 = \text{gcd}(a_1, b_1) \]

という形になる。この変形をユークリッドの互除法と同様に $b_k = 0$ となるような整数$k$まで繰り返すと、$k - 1$ の時点において次の関係式が得られる。

\[ a_{k-1} x_{k-1} + b_{k-1} y_{k-1} = b_{k-1} \]

この式の最も単純な解は $x_{k-1} = 0$, $y_{k-1} = 1$ である (通常、解は複数存在するが、RSA暗号にはそのうちの1つがあれば十分)。

ここから逆方向に変形をたどっていくことで、最初の方程式の解 $(x_0, y_0)$ を得ることができる。すなわち、$a_{i+1}, $b_{i+1}$, $x_{i+1}$, $y_{i+1}$が与えられている時、

\[\begin{split} \begin{align} a_i &= b_{i+1} \\ b_i &= a_{i+1} + m_i b_{i+1} \\ x_i &= y_{i+1} \\ y_i &= x_{i+1} - m_i y_{i+1} \end{align} \end{split}\]

のようにして、一つ前の $a_i$, $b_i$, $x_i$, $y_i$ を計算することができる。ここまでの一連の処理をプログラムとして実装する際には再帰関数をうまく用いるとよいだろう。

話をRSA暗号に戻そう。

ここまでの拡張ユークリッドの互除法で、$a=E, b=L$とすると$\text{gcd}(E, L) = 1$ であることから、

\[ Ex + Ly = 1 \]

が成り立つ整数 $x$, $y$ を求めることができる。

一度、そのような　$x$, $y$ が求まったら、両辺について$L$による剰余をとると、

\[ Ex \equiv 1 \pmod L \]

となるため、拡張ユークリッドの互除法で求めらた $x$ がRSA暗号によって求めたい $D$ であることが分かる。

なお、一連の計算では $x$ が負の値となることもあるため、この場合には、正の数になるまで $L$ を加えて値を調整する。

ユークリッドの互除法#

ユークリッドの互除法 は、2つの自然数の最大公約数を求める手法である。自然数$a, b$を考えた時、ユークリッドの互除法による最大公約数の導出は以下の手順となる。

$a \mod b = r_0$
$b \mod r_0 = r_1$
$r_0 \mod r_1 = r_2$
:
$r_i \mod r_{i+1} = 0$
剰余がゼロとなる時の $r_{i+1}$ が、$a, b$の最大公約数である。

練習問題

拡張ユークリッド互除法により$x$, $y$の組を求める関数 egcd(a, b) を作成しなさい。

練習問題

以下は、RSA暗号を簡易的に模擬したプログラムである。「各自作成」となっている箇所を埋めて、完成させよう。

なお、前述のとおり平文 $T_p$ は、$N$未満である必要がある。以下の実装例では、文字列が小文字アルファベットだけを含むとして文字列を整数に直す関数を用いているが、これでも暗号化できる平文の長さには限界があることに注意してほしい。

6.4. 通信ネットワークと暗号化#

冒頭にも述べたように、インターネット上では機密性の高い情報が日々やりとりされている。たとえば、Amazonや楽天のようなオンラインショップで、支払いのためにクレジットカード情報を入力したことがある人も多いだろう。

もし、入力した内容を悪意ある第三者が読み取ることができてしまったら、不正利用されるおそれがある。そうした事態を防ぐために、ウェブの閲覧は SSL (Secure Sockets Layer) / TLS (Transport Layer Security) によって暗号化されている。 SSL/TLS等によって暗号化されたHTTP通信を HTTPS通信 と呼ぶ（HTTPS自体はプロトコルではなく、セキュアなHTTP通信に対する呼称である）。

HTTPリクエストの回で説明したように、HTTPはクライアント（ウェブブラウザ）がウェブサーバに対してコンテンツを要求し、レスポンス（HTMLファイル等）を受け取るためのプロトコルである。

受け取ったHTMLファイル等をブラウザが解釈して表示（レンダリング処理という）したものが、普段目にしているウェブページである。従って、HTTPS通信では、リクエストやレスポンスの中身が暗号化されることとなる。

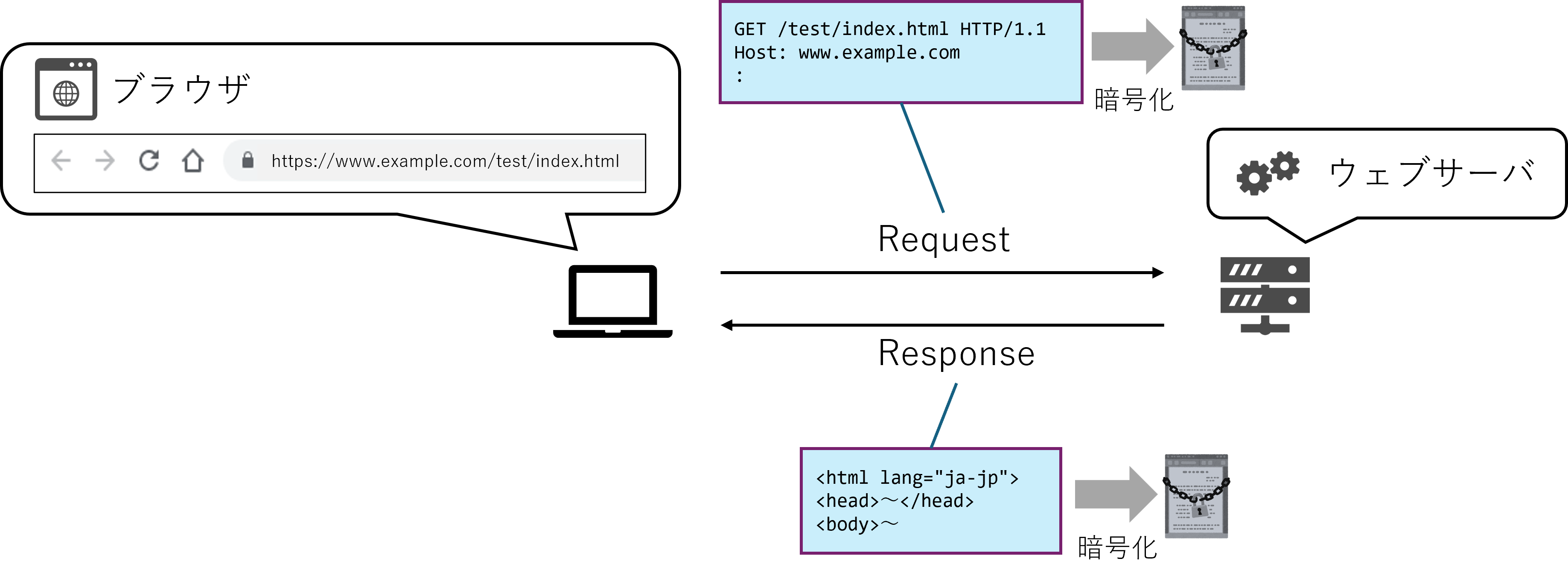
../../_images/https.png — 図 6.2 HTTPS通信の概念図#

Google透明性レポートによれば、Windows, Mac, Android上でのGoogle ChromeによるHTTPS利用率（グローバル）は2025年現在90%以上となっている。

また、Google Chromeをはじめとして、非HTTPS接続に対して警告を表示する機能を持つブラウザも増えてきており、ウェブサーバ運用時にはHTTPS対応が必須の状況となりつつある。

以降では、SSL/TLSの要素技術である 暗号学的ハッシュ関数、 電子署名 ならびに 電子証明書 について述べた後、SSL/TLSの説明をおこなう。

暗号学的ハッシュ関数#

ハッシュ関数 とは、任意のデータを入力として、固定長のビット列を出力する関数であり、出力として得られるビット列を ハッシュ値 と呼ぶ。ハッシュ関数には、通常、 同じ入力に対しては、必ず同じ出力を返す という性質がある。

原始的なハッシュ関数として、剰余を使う方法がある。以下は、入力データに対して100による剰余をとるハッシュ関数の例である。

N = 100

def hash(data):
    """ dataは整数 """
    return data % N

表 6.3 入力の整数と対応するハッシュ値#
入力	出力
123	23
12345	45
1234567	67

このように、計算結果は入力データの長さとは無関係に0から99の範囲となり、同じ入力に対しては常に同じ出力となる。

ハッシュ関数の典型的な利用例にはハッシュテーブルがある。ハッシュテーブルは <key, value> 形式のデータを格納するデータ構造であり、keyのハッシュ値によってメモリ上の格納位置を決める。例えば、Pythonの辞書型 (dict) はハッシュテーブルにより実装されている。

ハッシュ値を計算すれば格納位置が求まり、メモリ上を探索する必要がないため、データの参照や追加を高速に行える利点がある（実際には、ハッシュ値の衝突が起こるとメモリ上を探索する必要が生じるが、ここでの説明は割愛する）。

暗号学的ハッシュ関数 とは、ハッシュ関数の一種であり、特に以下の3つの性質を満たすものを指す。

ハッシュ値Hから元の入力データAを求めることが困難（一方向性, 原像計算困難性）
入力データAとハッシュ値Hの組から、ハッシュ値が一致する別の入力データBを求めることが困難（弱衝突耐性, 第2原像計算困難性）
同じハッシュ値Hが得られる入力データのペアA, Bを発見することが困難（強衝突耐性）

これらを満たすような暗号学的ハッシュ関数は、入力データがわずかでも異なれば、全く異なるハッシュ値を返す。入力と出力に一見してわかるような相関があれば、ハッシュ値から入力を推測することが容易にできてしまうためである。

多少疎かな理解にはなるが、暗号学的ハッシュ関数は 任意のデータから固定長の乱数を出力する ものと捉えることもできる。代表的な暗号学的ハッシュ関数には MD5 (Message Digest Algorithm 5) や SHA (Secure Hash Algorithm) が挙げられる。

暗号学的ハッシュ関数は、その性質から、データの指紋やIDのようなものと見なすことができる。人間の指紋は、個人ごとに紋様が異なり（万人不同）、生涯変わることがない（終生不変）とされている。暗号学的ハッシュ関数により得られたハッシュ値も似た性質を持ち、データごとに固有である。この性質を活かして、 データの改ざん検出 等に用いられる。

練習問題7

LinuxのコマンドにはMD5を計算する md5sum や SHA-256を計算する sha256sum がある。適当なテキストファイルを用意したうえで、そのファイルのMD5およびSHA-256ハッシュ値を計算してみよう。

# 実行例
$ echo "Hello, world." > hello1.txt
$ md5sum hello1.txt
$ echo "Hello, world!" > hello2.txt
$ md5sum hello2.txt

電子署名（デジタル署名）#

電子署名（デジタル署名） とは、電子データに対する捺印や署名のようなものであり、以下を実現する技術である。

同一性の確認: データが改ざんされていないかどうか
本人性の確認: 署名をしたのはたしかに本人であるか

送信者による電子署名の作成と、受信者による電子署名の検証は、それぞれ以下の手順でおこなわれる (図 6.3 参照)。

電子署名の作成
1. 送信したい電子データのハッシュ値を計算
2. ハッシュ値を秘密鍵で暗号化
3. 暗号化したハッシュ値を電子データに添付（署名）し、送信
電子署名の検証
1. 受信した電子データのハッシュ値を計算
2. 電子署名を署名者の公開鍵で復号
3. 2で得られたハッシュ値を、1のハッシュ値と比較

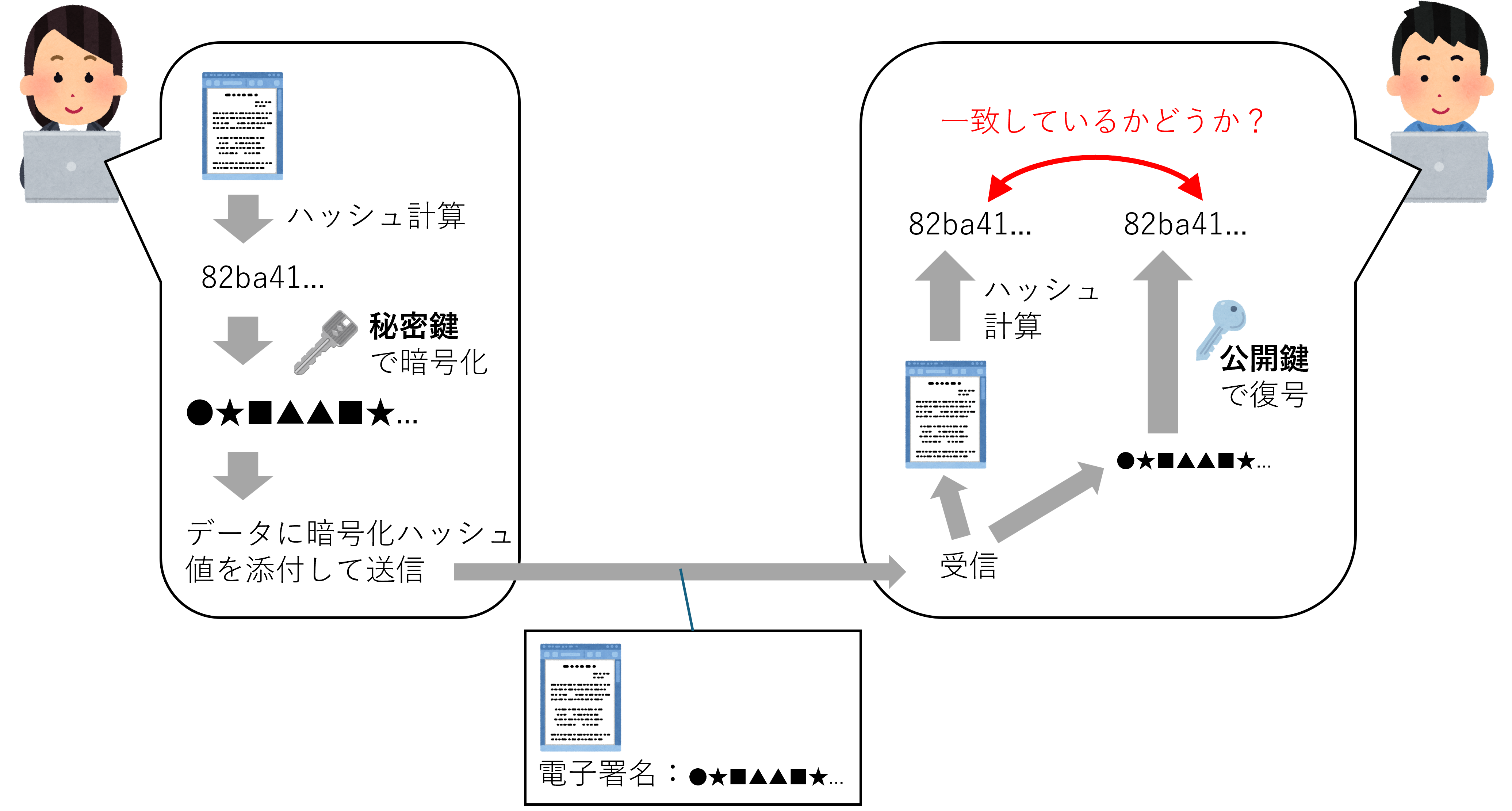
../../_images/e-sig.png — 図 6.3 電子署名による同一性および本人性の確認の概念図#

前述の公開鍵暗号方式では、公開鍵を用いて暗号化し、秘密鍵で復号をおこなっていた。実は、公開鍵暗号における鍵ペアは、逆の組み合わせで用いることもできる（3.1節の例で試してみると良い）。すなわち、 秘密鍵で暗号化したものを、公開鍵で復号 することができる。

この場合も性質は変わらず、秘密鍵で暗号化された暗号文は、対応する公開鍵でなければ正しく復号することはできない。電子署名はこの性質を応用したものであり、 秘密鍵という本人しか持たない情報によってデジタルな署名をおこなう 仕組みである。

検証のステップ3において、2つのハッシュ値が一致している場合、以下の2点を確認できたことになる。

復号に用いた公開鍵と対応する秘密鍵の持ち主により作成されたものであること
その作成時の内容から改ざんが為されていないこと

1については、電子署名を公開鍵によって復号できることが、それすなわち、公開鍵と対応する秘密鍵で署名が暗号化されていることを意味する。従って、署名を作成したのは秘密鍵を持つ本人であると確認できる。

2については、送受信したファイルのハッシュ値の一致をもって改ざんがなされていないことを確認できる。暗号的ハッシュ関数の性質から、情報が少しでも異なれば全く異なるハッシュ値が得られるため、もし内容が少しでも改ざんされていればハッシュ値は一致しないはずである。

このときにポイントとなるのは、秘密鍵を用いた暗号化によって作成される電子署名自体はいくら複製されても問題がない、という点である。なぜなら、電子署名自体が複製されたとしても、秘密鍵を入手しない限りは、悪意のある第三者が勝手に新たな電子署名を作成することはできないからである。

ただし、電子署名の仕組みだけでは、公開鍵が本物かどうか という問題は残る。つまり、悪意のある第三者が、送信者を偽って偽物の公開鍵と秘密鍵のペアを作成し、送信者になりすまして電子署名を作成していた場合には、受信者はそれを見抜くことができない。

これを解消するための仕組みが、次に紹介する 電子証明書 である。

電子証明書#

電子証明書 は、電子署名と署名者の対応関係に係る証明書であり、特に公開鍵とその所有者との紐づけを証明するものを 公開鍵証明書 、公開鍵証明書の発行を実現する典型的な仕組みを 公開鍵基盤 (Public Key Infrastructure, PKI) と呼ぶ。

公開鍵証明書は、 認証局 から購入することができる。代表的な認証局としてGlobalSignやDigiCert等がある。また、無料で証明書を発行できるLet's Encrypt等のサービスも存在する。

公開鍵証明書には、以下のような情報が含まれる。

主体者（公開鍵の所有者）
公開鍵
有効期限
発行者（認証局）
発行者の電子署名

これらの情報はブラウザから誰でも簡単に確認することができ、実際に日本銀行のウェブサイトで公開鍵証明書を確認してみると、次のような情報が確認できる。

../../_images/boj_cert.jpg — 図 6.4 公開鍵証明書の例 (日本銀行のウェブサイト: https://www.boj.or.jp/)#

このように第三者機関が公開鍵証明書が本物であることを証明していれば、記載されている公開鍵がたしかにその主体者のものであると確信を持って電子署名の検証などが行える。これで、前述の「公開鍵が本物かどうか」という懸念も解消できた。

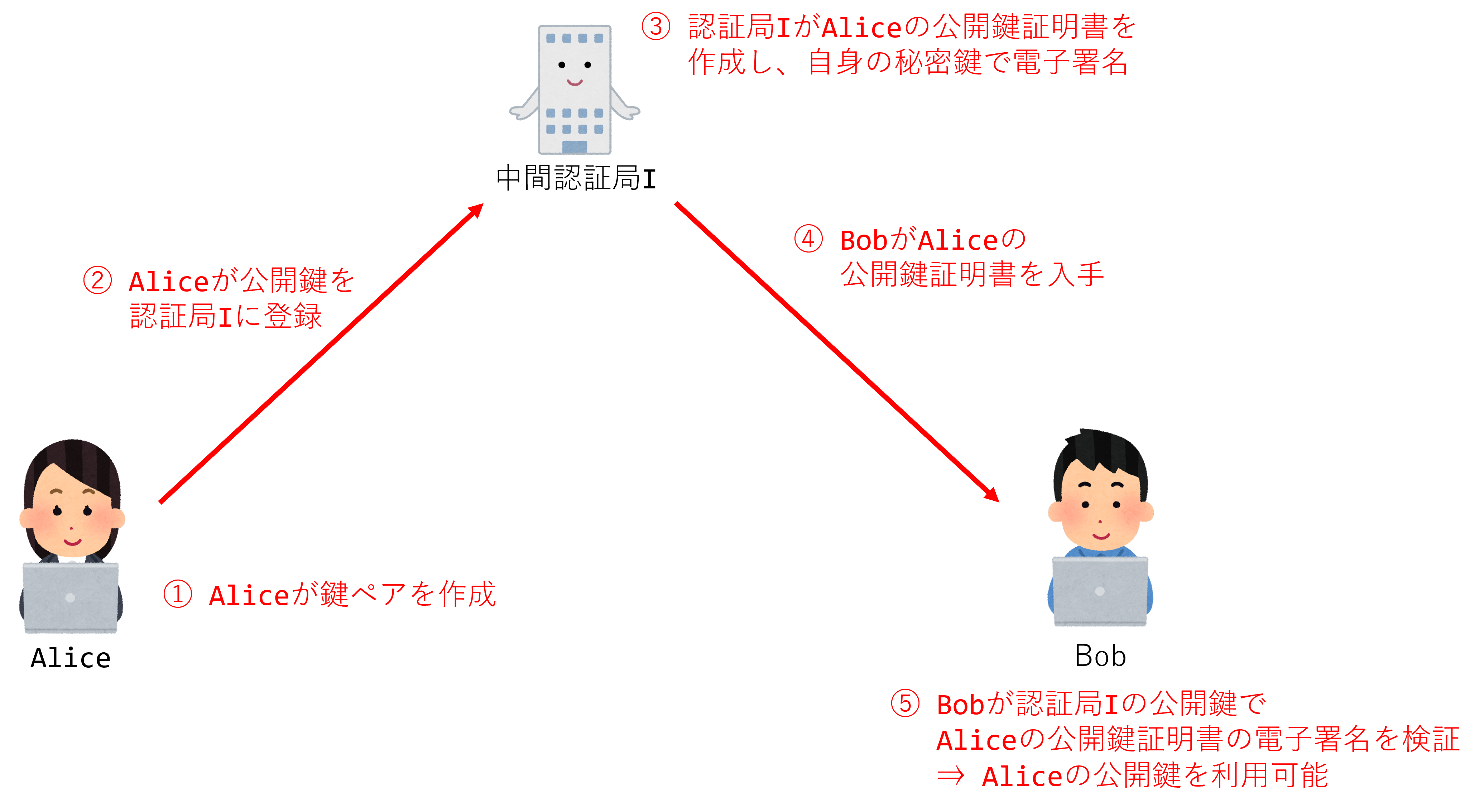
しかし、図 6.4 に示した証明書ビューアをよく見てみると、「詳細」というタブから証明書の階層構造を確認できることが分かる。

実は、とある電子証明書が本物であると証明している機関が本物であることが、さらに上位の認証局によって証明されていて、この証明・被証明の関係が階層構造になっているのである。この仕組みにより、悪意のある第三者が勝手に偽物の認証局を立ち上げて、電子証明書を発行することを防いでいる。

このような認証局の階層において、最上位に位置する認証局を ルート認証局 、その下位に位置する認証局を 中間認証局 と呼ぶ。

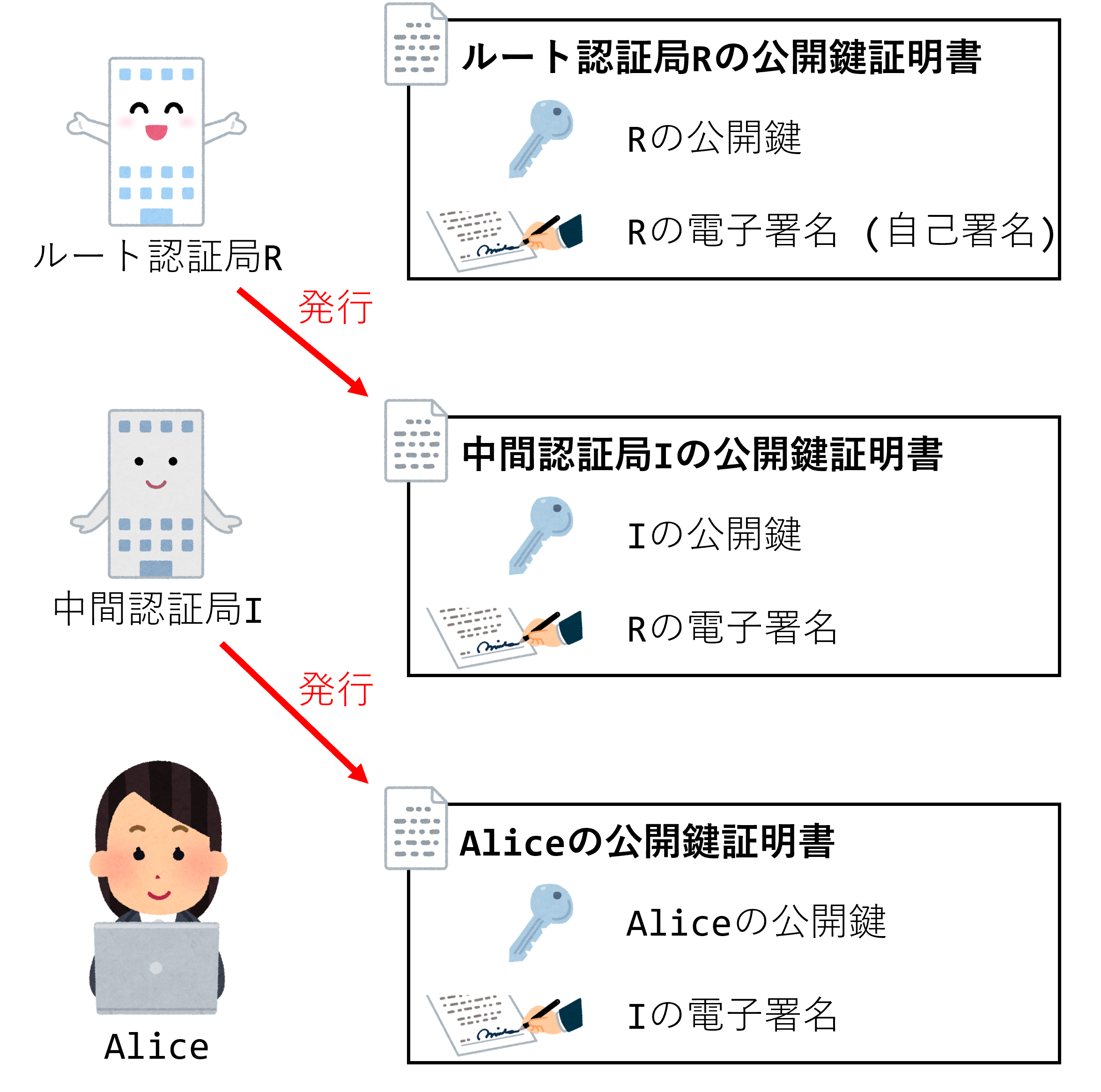
普段利用しているウェブブラウザには、主要なルート証明書（ルート認証局の公開鍵証明書）があらかじめ組み込まれている。このルート認証局の公開鍵で中間認証局の公開鍵の正しさを確認し、中間認証局の公開鍵でAliceの公開鍵の正しさを確認する、といった形で連鎖的に真正性の確認が為される（ 証明書チェーン ）。

SSL/TLS#

SSL (Secure Socket Layer) は1994年にNetscape社が開発したプロトコルであり、同社のウェブブラウザNetscape Navigator (後のFirefox)への導入を皮切りに多くのブラウザで採用されたことがきっかけで広く用いられるようになった。

TLS (Transport Layer Security) は、SSL 3.0を元にしてIETF (Internet Engineering Task Force)が策定したSSLの後継プロトコルである。実際、SSLには脆弱性があることが明らかとなっており、現在では利用すべきではないものとなっている。そのため、現在HTTPSで用いられているのはTLSであるが、SSLの名称が広く普及していたことから、「SSL/TLS」のように併記したり、SSLとTLSを総称して「SSL」と呼ぶ場合も多い。

TLSは、電子署名により 通信相手の認証 (= サーバが本物かの確認) をおこない、ハイブリッド暗号等により (認証されたクライアントしか閲覧できないように) 通信内容の暗号化 を行う。同時に、メッセージ認証コードにより改ざん検出を行う仕組みも持つが詳細は割愛する。

TLSによる暗号化通信のおおまかな処理の流れは次の通りである。

通信の疎通確認
1. クライアント（PC等）はサーバ（ウェブサーバ等）に通信開始要求を送る（Client Hello）
2. サーバはクライアントに応答を送る（Server Hello）
  - Client Hello/Server Helloのやりとりの中で、使用する暗号アルゴリズム等を決定
  - この段階では通信内容は暗号化されていない
公開鍵の取得と検証
1. サーバはクライアントに電子証明書を送付する
2. クライアントはサーバから送付された電子証明書の検証を行い、サーバの公開鍵が本物かどうかを確認する
  - この段階でも通信内容は暗号化されていない
共通鍵の共有 (RSA暗号を用いる場合)
1. クライアントは適当な乱数を生成し、これを以後の共通鍵暗号で使用する共通鍵とする
2. 共通鍵を検証済みのサーバの公開鍵で暗号化し、サーバへと送信する
3. 暗号化された共通鍵を受信したサーバは、自身の秘密鍵を用いて共通鍵を復号する
暗号化通信
1. Webページなどの情報がクライアントの発行した共通鍵によって暗号化され、クライアントへと送付される
2. 暗号化された情報を受け取ったクライアントは、自身の共通鍵を用いて情報を復号する

なお、2018年にリリースされたTLS1.3では、前方秘匿性の観点からRSA暗号による鍵交換は廃止され、Diffie-Hellman鍵交換法だけが使用されるようになっている。

6.5. 課題#

問1

RSA暗号における秘密鍵$D$の計算は、前述の拡張ユークリッド互除法を用いる方法以外に、
$E \times D \equiv 1 \pmod L$
を満たす数を順番に探していく総当たり的な方法も考えられる。プログラムは以下のとおりである。

def getD(p, q, e):
    L = lcm(p-1, q-1)
    d = 1
    while True:
        if (e * d) % L == 1:
            return d
        d += 1

上記のプログラムと、拡張ユークリッド互除法を用いるプログラムの、処理時間の違いを調べなさい。
以下の4パターンの素数の組について、両方式それぞれの所要時間を計測して回答すること。所要時間はプログラム内で計測し、単位を明記すること。

10007, 10009
20011, 20021
30011, 30013
40009, 40013

なお、30秒程度待ってもプログラムが終了しない場合は、実行を打ち切って良い。
その場合、回答欄には「N/A」と記入すること。

問2

ex2_file1.txt および ex2_file2.txt の2つのファイルがある。今、この2つのファイルのうち、どちらか一方が悪意のある第三者によって改ざんされている。

しかし、これらのファイルには幸運にも善意の送信者による電子署名が付与されていた。

電子署名： 2466594619 （※10進数）

電子署名はRSA暗号を用いて行われており、公開鍵である整数 $E$, $N$ の組は次のとおりであった。

E： 1329863093 （※10進数）
N： 4900280003 （※10進数）

これらの情報をもとにどちらのファイルが改ざんされているかを特定しなさい。

ただし、本課題におけるハッシュ値は、簡単のためにSHA256の前方4byte分のみを用いることとする。

【例】 SHA256によるハッシュ値：e8fd936345e0a40a277818d1abc8b9c1bd07631c9bd90f7a8e2d1fb8280eae9c 本課題で使うハッシュ値：e8fd9363　（※10進数表記：3908932451）

問3（おまけ）

ex3.txt は、シーザー暗号による暗号文である。ただし、通常のシーザー暗号とは異なり、若干の工夫を加えてある。なお、暗号化されているのは英小文字のみである（大文字や記号は平文のまま）。

ex3.txtの暗号文を解読し、平文を回答しなさい。（解読作業にプログラムをどの程度使うかは任意。平文が得られればOK）

【ヒント】
英文で、1文字のみの単語は限られる。1文字単語はどのような文字に置き換わっているだろうか。

6.6. 参考文献#

『暗号技術入門第3版』結城浩著, SBクリエイティブ, ISBN: 978-4-7973-8222-8
『マスタリングTCP／IP入門編第6版』井上直也ほか著, オーム社, ISBN: 978-4-274-22447-8