2. 図形の検出

OpenCV を用いて画像中から図形を検出してみよう。図形の検出は、画像からのエッジの情報を取り出す処理と、エッジ情報を元に境界線を認識する処理、境界線から図形の形状を分類する処理の三つに分けられる。

さらに、実写真から図形を取り出す場合には、いわゆるパースを考慮した図形の検出が必要になる。

2.1. 単純図形の検出

まず手始めに、以下の単純な図形が描かれた画像を題材として、図形の検出方法を見てみる。

2.1.1. エッジの検出

「OpenCV の基本」で、紹介したように、画像からエッジの情報を得るアルゴリズムにはSobel フィルタやCanny フィルタがある。

これらのフィルタを画像に適用した後、候補となる画素の中で勾配が一定以上となる場所を閾値処理により取り出す二値化処理を施すことで、最終的なエッジが得られる。

以下が OpenCV で Sobel フィルタと Canny 法によりエッジ画像を得るプログラムと、その結果である。なお、Canny フィルタは直接、二値画像を出力するため、二値化の処理は Sobel フィルタの結果だけに適用している。

import cv2
import numpy as np

# 画像の読み込み
image = cv2.imread("../../data/figures.png", cv2.IMREAD_COLOR)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)

# 画像をグレースケールにする
gray = cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)

# Sobelフィルタ
dx = cv2.Sobel(gray, cv2.CV_8U, 1, 0)
dy = cv2.Sobel(gray, cv2.CV_8U, 0, 1)
sobel = np.sqrt(dx * dx + dy * dy)
sobel = (sobel - sobel.min()) / (sobel.max() - sobel.min())
sobel = (sobel * 255.0).astype("uint8")
_, sobel = cv2.threshold(sobel, 10, 255, cv2.THRESH_BINARY)

# Canny法
canny = cv2.Canny(gray, 100, 200)

なお、上記のプログラム中の cv2.thresholdは 8 ビット符号なし整数(0 から 255 の値)で画素が表わされているグレースケール画像に対して、閾値による二値化処理を行う関数である。上記の例では、グレースケール画像 sobelに対して、画素値が 10 以上であれば白とみなす、という処理を行っている。

Show code cell source Hide code cell source

import matplotlib.pyplot as plt

fig = plt.figure(figsize=(15, 5))
ax = fig.add_subplot(131)
ax.imshow(image)
ax.axis("off")

ax = fig.add_subplot(132)
ax.imshow(sobel, cmap="gray")
ax.axis("off")

ax = fig.add_subplot(133)
ax.imshow(canny, cmap="gray")
ax.axis("off")

plt.tight_layout()
plt.show()

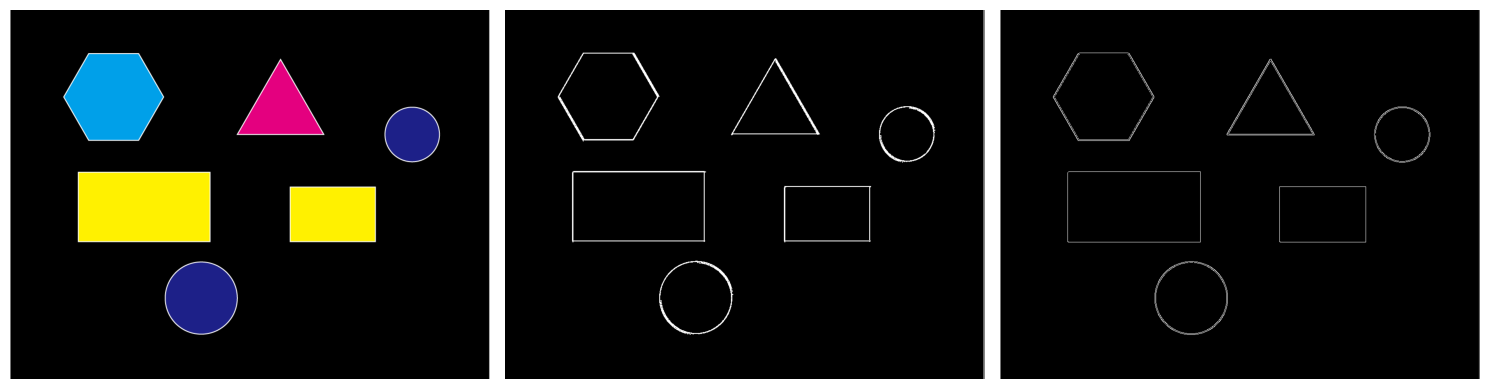
2.1.2. エッジの統合

結果を見てみると、上記の入力画像は図形の輪郭線が幅を持つため、エッジが二重線で検出されていることが分かる。もちろん、これで間違いとは言えないが、エッジが内側の線と外側の線の間で曖昧に検出されており、この後の輪郭線検出に影響を及ぼす可能性がある。この問題は自然画像を入力とする場合には、より顕著となる。

そこで、輪郭線を抽出する前に、モルフォロジー演算によりエッジの統合を行っておく。モルフォロジー演算は一般的には二値画像を入力として、白色の領域を広げたり狭めたりする操作である(モルフォロジー演算の数学的な意味とは解釈が異なるので注意)。今回は白色領域を広げる処理である dilation と白色領域を狭める処理である erosion を連続して施すことでエッジの統合を行う。

モルフォロジー演算は構造要素と呼ばれる小さな画像のようなものを入力の二値画像にしたがって繰り返す操作に対応する。したがって、OpenCV(や MATLAB などの他のライブラリ)では、モルフォロジー演算の関数は二値画像と構造要素を引数にとる。OpenCV を用いる場合には、dilation と erosion はそれぞれ以下のようなコードで実現される。

binary = sobel.copy()
res_dilate = cv2.dilate(binary, np.ones((5, 5), dtype=binary.dtype))
res_erode = cv2.erode(binary, np.ones((5, 5), dtype=binary.dtype))

Show code cell source Hide code cell source

fig = plt.figure(figsize=(8, 4))
ax = fig.add_subplot(121)
ax.imshow(res_dilate, cmap="gray")
ax.set_title("Dilation")
ax = fig.add_subplot(122)
ax.imshow(res_erode, cmap="gray")
ax.set_title("Erosion")
plt.tight_layout()
plt.show()

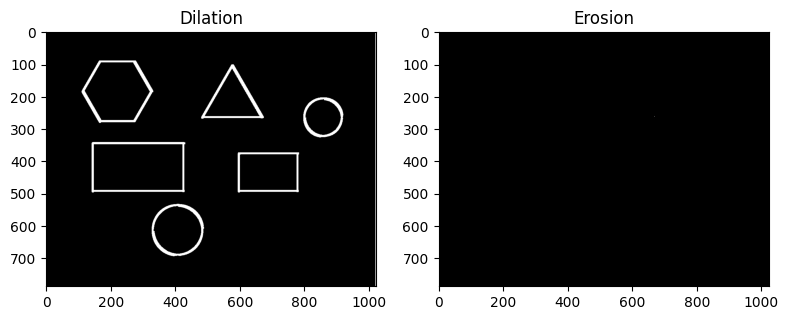
エッジを統合する場合、エッジが白色の領域に検出されているとすると、先に dilation、次に erosion の順序で処理を施す。dilation により二重のエッジのそれぞれが太くなり、重なることで、太い 1 本のエッジとなる。その後、erosion をかけることで、そのエッジが細くなり、1 本の細いエッジとなる。

res = sobel.copy()
res = cv2.dilate(res, np.ones((5, 5), dtype=binary.dtype))
res = cv2.erode(res, np.ones((5, 5), dtype=binary.dtype))

Show code cell source Hide code cell source

plt.imshow(res, cmap="gray")
plt.show()

上記の結果の通り、dilation と erosion を組み合わせることで二本の細いエッジが一本のエッジに統合されていることが分かる。

なお dilation の後に erosion をする操作を特にclosingと呼び、反対に erosion の後に dilation をする操作をopeningと呼ぶ。白色の輪郭線を統合する処理はclosingに対応しており、以下のコードでも同じことができる。

binary = sobel.copy()
res_close = cv2.morphologyEx(binary, cv2.MORPH_CLOSE, np.ones((5, 5), dtype=binary.dtype))

Show code cell source Hide code cell source

plt.imshow(res_close, cmap="gray")
plt.show()

2.1.3. 輪郭線の検出

ここまでに検出したエッジの情報を使って輪郭線を抽出する。輪郭線の抽出には OpenCV の findContoursという関数を用いる。この関数には 1985 年に Suzuki さんと Abe さんという日本人が提案したアルゴリズムが実装されている[Suzuki and Abe, 1985]。

このアルゴリズムは二値画像(1 がエッジで 0 が背景の色とする)をラスタスキャン (最初の列を左から右に見ていき、右端に到達したら、左から右に見ていく、以後繰り返し) していき、1 が見つかったら、その画素から始まる輪郭線を追跡する。

輪郭線の追跡は、今見ている画素の周りを時計回りに見ていき、初めて 1 となる画素にスキャン位置を移動する、という操作を繰り返すことで行われる。端点に到達するか、元の位置の画素に戻ってきたら、再びラスタスキャン順に値が 1 の画素で、まだどの輪郭にも含まれていない画素を探し、以後、同様の処理を繰り返していく。

OpenCV の findContoursは 3 つの引数を取り、第 1 引数が入力の二値画像、第 2 引数が検出される輪郭線の階層関係、第 3 引数が抽出する輪郭線をどのように近似表現するかを表す。代表的な使い方は以下の通り。

contours, _ = cv2.findContours(
    res_close,
    cv2.RETR_EXTERNAL,
    cv2.CHAIN_APPROX_SIMPLE,
)

第 2 引数のcv2.RETR_EXTERNALは二重丸のような階層的な輪郭線が現れたときに最も外側の閉曲線のみを抽出する。また第 3 引数のcv2.CHAIN_APPROX_SIMPLEは抽出される輪郭線が 0 度(=水平)、90 度(=垂直)、45 度, 135 度の向きに直線的につながるときに、それらを端点だけで近似することを表わす。

この他の使い方については公式のドキュメントを参考にしてほしい。

2.1.4. 輪郭線の描画

上記の方法で検出された輪郭線はfindContoursと対になるdrawContoursで描画できる。この関数は以下の引数を取る。

• 第 1 引数: 描画先の画像

• 第 2 引数: findContoursで検出された輪郭線

• 第 3 引数: 配列中の何番目の輪郭線を描画するか (-1 は全て描画する)

• 第 4 引数: 輪郭線を描画する色

• 第 5 引数: 輪郭線を描画する太さ

• 第 6 引数: 輪郭線の描画スタイル (cv2.LINE_AAはアンチエイリアシングを行う)

こちらも詳しい使い方は公式のドキュメントを参考にしてほしい。

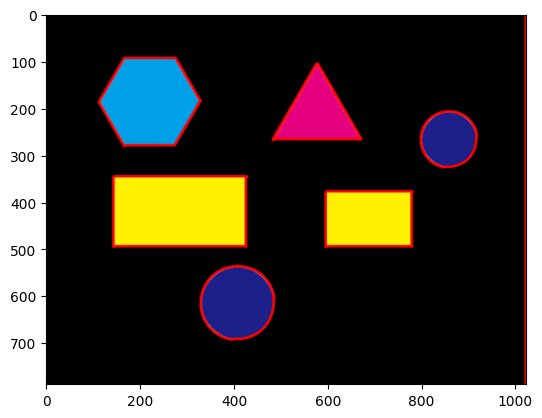
実際に上記の方法で検出した輪郭線を描画してみたものが以下である。見ての通り、各図形の外側と画像自体の輪郭に輪郭線が検出されていることがわかる。

cv2.drawContours(image, contours, -1, (255, 0, 0), 3, cv2.LINE_AA)
plt.imshow(image)
plt.show()

2.1.5. 輪郭線の分類

各輪郭線がどのような図形か(円か？多角形か？そうなら何角形か？)を判別するには、輪郭線を多角形として近似して、その頂点の数を調べれば良い。

findContours で検出された輪郭線 (cv2.CHAIN_APPROX_SIMPLEを使った場合)は特定の向きの直線のみを端点で近似している。そのため、現在検出されている多角形は、必ずしも角の点だけで表されているわけではない。実際、contours[i]の長さを見てみると、六角形なども直線が複数の点で表わされているために、6 個以上の頂点を含むことが分かる。

そこで、検出されている輪郭線を更に粗く角の点だけで近似することを考える。これには OpenCV のcv2.approxPolyDPという関数が使える。この関数の接尾語になっている DP は Douglas-Peucker の頭文字であり、内部ではRamer-Douglas-Peucker 法というアルゴリズムが使われている。

実際にfindContoursで検出した各輪郭線をapproxPolyDPを用いて近似してみる。

for i, cnt in enumerate(contours):
    # 輪郭線の長さを計算
    arclen = cv2.arcLength(cnt, True)
    # 輪郭線の近似
    approx = cv2.approxPolyDP(cnt, 0.01 * arclen, True)
    # 何角形かを見てみる
    print("Figure #{:d} has {:2d} corners!".format(i + 1, len(approx)))
    # 輪郭線の描画
    cv2.drawContours(image, [approx], -1, (255, 0, 0), 3, cv2.LINE_AA)

Figure #1 has 13 corners!
Figure #2 has  4 corners!
Figure #3 has  4 corners!
Figure #4 has 15 corners!
Figure #5 has  3 corners!
Figure #6 has  6 corners!
Figure #7 has  2 corners!

上記のコードでは cv2.arcLength を使って曲線の長さを計算し、その長さの 100 分の 1 の精度を持つように輪郭線を近似している。この精度はあまり細かすぎると角が増え、粗過ぎても角が減ってしまうので、多少の調整が必要ではある。print で出力された内容を見てみると 6 や 4 といった角の数と思われる数字が得られていることが分かる。

Ramer-Douglas-Peucker法

このアルゴリズムは、ある図形を適当な離散点(開曲線なら端点)を選んでその間を直線で結んだときに、最も離れている点を順次追加してポリライン(直線を結んで曲線を近似したもの)を更新していく。最も離れた点までの距離が一定以下になったら処理を終える。閉曲線の場合には、すべての候補となる点の中で最も離れた2点を見つけ、その二点を直線で結んで、二点の上部と下部を別々のポリラインで近似する (以下のアニメーションを参照)。

Show code cell source Hide code cell source

from IPython import display
from matplotlib.animation import ArtistAnimation


def curve(x):
    y = x**3 - x
    return y


def dist_p2l(px, py, x0, x1, y0, y1):
    vx = x1 - x0
    vy = y1 - y0
    length = np.sqrt(vx**2 + vy**2)
    if length == 0.0:
        return np.sqrt((px - x0) ** 2 + (py - y0) ** 2)

    vx /= length
    vy /= length
    dot = vx * (px - x0) + vy * (py - y0)
    if dot < 0.0:
        return np.sqrt((px - x0) ** 2 + (py - y0) ** 2)

    if dot > length:
        return np.sqrt((px - x1) ** 2 + (py - y1) ** 2)

    x_proj = x0 + vx * dot
    y_proj = y0 + vy * dot
    return np.sqrt((x_proj - px) ** 2 + (y_proj - py) ** 2)


fig = plt.figure()
plt.gca().set_aspect("equal")
plt.xlim(-1.0, 1.0)
plt.ylim(-1.0, 1.0)

xs = np.linspace(-1.0, 1.0, 50, endpoint=True)
ys = curve(xs)

px = [xs[0], xs[-1]]
py = [ys[0], ys[-1]]

# Render frames
frames = []
num_frames = 9
for i in range(num_frames):
    # Draw the current frame
    # plt.clf()
    pts = plt.scatter(px, py, color="tab:red", zorder=2)
    lns = plt.plot(px, py, color="tab:blue", linestyle="--", zorder=1)
    frame = plt.plot(xs, ys, color="tab:blue", zorder=0)
    frames.append([pts] + lns + frame)

    # Find the point farthest from the current polyline
    ds = np.full_like(xs, np.inf)
    for x0, x1 in zip(px, px[1:]):
        for y0, y1 in zip(py, py[1:]):
            temp_ds = np.array([dist_p2l(x, y, x0, x1, y0, y1) for x, y in zip(xs, ys)])
            ds = np.minimum(ds, temp_ds)

    max_idx = np.argmax(ds)

    # Sort point coordinates
    px.append(xs[max_idx])
    py.append(ys[max_idx])
    idx = np.argsort(px)
    px = [px[i] for i in idx]
    py = [py[i] for i in idx]

# Convert animation to HTML+JS
ani = ArtistAnimation(fig, frames, interval=1000, blit=True)
html = display.HTML(ani.to_jshtml())
display.display(html)
plt.close()

Once Loop Reflect

---

角の数が正しく得られていることが分かったら、頂点の数を数えて、図形の種類を判別する。ここでは、10 個以上の頂点を持つ場合は円であると見なす。

n_gon = len(approx)
text = "unknown"
if n_gon > 10:
    text = "circle"
elif n_gon == 6:
    text = "hexagon"
elif n_gon == 5:
    text = "pentagon"
elif n_gon == 4:
    text = "rectangle"
elif n_gon == 3:
    text = "triangle"

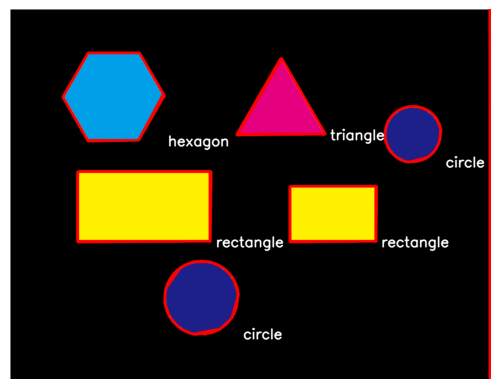
この判別結果を画像中にテキストとして書き込む。OpenCV に用意されたputTextを用いる。以下のコードでは、contoursに格納された輪郭線一つ一つについて、何角形かを判定して、その輪郭線と種類を表わすテキストを順に描画している。

result = image.copy()
font = cv2.FONT_HERSHEY_SIMPLEX

for cnt in contours:
    arclen = cv2.arcLength(cnt, True)
    approx = cv2.approxPolyDP(cnt, arclen * 1.0e-2, True)
    cv2.drawContours(result, [approx], -1, (255, 0, 0), 3)

    n_gon = len(approx)
    text = "unknown"
    if n_gon > 10:
        text = "circle"
    elif n_gon == 6:
        text = "hexagon"
    elif n_gon == 5:
        text = "pentagon"
    elif n_gon == 4:
        text = "rectangle"
    elif n_gon == 3:
        text = "triangle"

    position = np.asarray(approx).reshape((-1, 2)).max(axis=0).astype("int32")
    px, py = position
    cv2.putText(result, text, (px + 10, py + 10), font, 1.0, (255, 255, 255), 2, cv2.LINE_AA)

Show code cell source Hide code cell source

plt.imshow(result)
plt.axis("off")
plt.show()

問題

Ramer-Douglas-Peucker のアルゴリズムでは、「開曲線」を線分の集合により近似する方法を紹介した。では、閉曲線に対して、同アルゴリズムを適用するにはどうすれば良いか。

2.2. 実写真からの図形の検出

続いては、以下の駅の写真から看板を抜き出してみよう。

単純図形の時と同じように輪郭線を抜き出そう。ただし、今回は自然画像であり、含まれる画像の色が様々なので少し工夫が必要になる。

2.2.1. 画像の前処理

まず、エッジを抜き出す際には、細かな輝度の変化はそれほど重要ではなく、大きな輝度の変化が起こる場所だけが分かれば良い。自然画像には多くの場合、細かなノイズがのっているので、最初にぼかしフィルタをかけてノイズを減らしておく。

次に、看板が白いことに注目して、グレースケール画像を先に二値化してしまう。この際、自動で閾値を決める方法に「大津の二値化」と呼ばれる方法がある。大津の二値化は画像を輝度のヒストグラムとして表わしたときに、2 つに分けられたヒストグラムのそれぞれが持つ色の分散をできる限り小さくするように閾値を決める。

image = cv2.imread("../../data/inawashiro.jpg", cv2.IMREAD_COLOR)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)

# ぼかし処理
gray = cv2.GaussianBlur(gray, None, 3.0)

# 大津の二値化
thr, binary = cv2.threshold(gray, 0, 255, cv2.THRESH_OTSU)

Show code cell source Hide code cell source

plt.imshow(binary, cmap="gray")
plt.title("Otsu's binarization (threshold={:d})".format(int(thr)))
plt.show()

大津の二値化では、上記のように「自然画像を自然なまま二値化」した画像が得られるため、より白い領域だけを残すように閾値を調整する。thresholdの第 1 戻り値は実際に二値化に用いた閾値であるため、これを少し大きくなるようにスケーリングして、再度二値化処理をかける。

new_thr = min(int(thr * 1.5), 255)
_, binary = cv2.threshold(gray, new_thr, 255, cv2.THRESH_BINARY)

plt.imshow(binary, cmap="gray")
plt.title("Binarization (threshold={:d})".format(int(new_thr)))
plt.show()

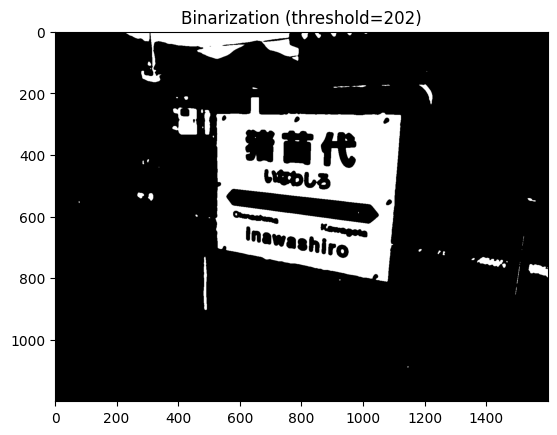
すると、上記のように看板の部分だけが強調されたような画像を得ることができる。

2.2.2. エッジの検出

二値化により前処理した画像から「基本図形」の時と同様にエッジを検出する。今回は Canny 法によりエッジを検出し、モルフォロジー演算で余計な輪郭線を除去する。この際、dilation と erosion で dilation 側の構造要素を少し大きめに取っておくと、エッジがはっきりと残る。

edge = cv2.Canny(binary, 150, 200)
edge = cv2.dilate(edge, np.ones((11, 11), dtype=edge.dtype))
edge = cv2.erode(edge, np.ones((9, 9), dtype=edge.dtype))

plt.imshow(edge, cmap="gray")
plt.title("After morphology operation".format(int(new_thr)))
plt.show()

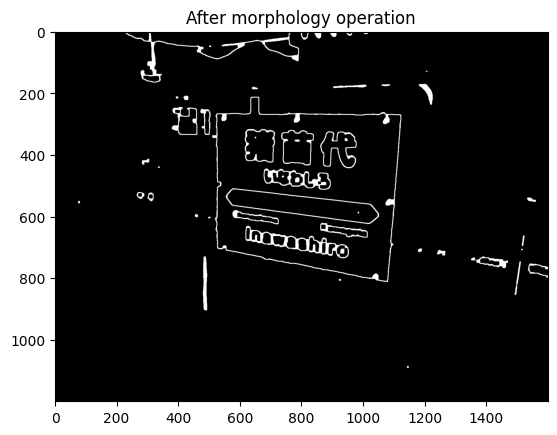
2.2.3. 図形の検出

看板を取り出すための方針として、写真に写っている物のうち、輪郭線が最も長いものが写真に写っている主要物体であると仮定する。この仮定に基づき、各輪郭線の長さを計算し、最も長い輪郭線だけを残す。

まずはfindContoursを使って、どのような輪郭線が抽出されるのかを確認する。仮定に基づいて処理を行う際には、考えた仮定が本当に成り立ちそうかを予め必ずチェックすること。

contours, _ = cv2.findContours(edge, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

result = image.copy()
cv2.drawContours(result, contours, -1, (255, 0, 0), 3, cv2.LINE_AA)
plt.imshow(result)
plt.show()

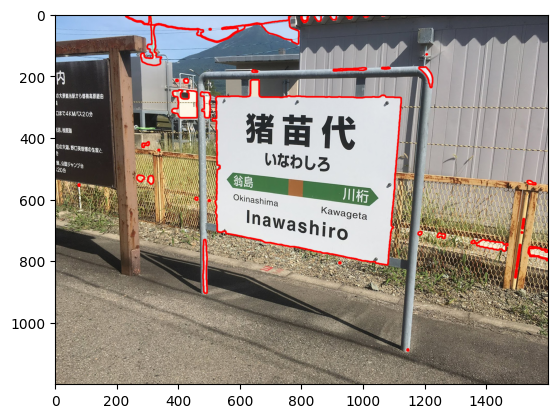
輪郭線の描画結果を見てみると、確かに一番長い輪郭線が看板を囲むものになっていそうに見える。実際に、輪郭線の長さを計算して、最も長い輪郭線がどれかを確認してみる。

longest_cnt = None
max_length = 0.0
for cnt in contours:
    # 輪郭線の長さを計算
    arclen = cv2.arcLength(cnt, True)
    if max_length < arclen:
        max_length = arclen
        longest_cnt = cnt

result = image.copy()
cv2.drawContours(result, [longest_cnt], -1, (255, 0, 0), 3, cv2.LINE_AA)
plt.imshow(result)
plt.show()

確かに最も長い輪郭線が看板に対応していることが分かったので、次に看板の四つ角を取ってくる。approxPolyDPを使い、短い辺を潰してしまうことで四角形を得ることができる。

arclen = cv2.arcLength(longest_cnt, True)
approx = cv2.approxPolyDP(longest_cnt, arclen * 1.0e-1, True)

result = image.copy()
cv2.drawContours(result, [approx], -1, (255, 0, 0), 3, cv2.LINE_AA)
plt.imshow(result)
plt.title("Red region has {:d} corners".format(len(approx)))
plt.show()

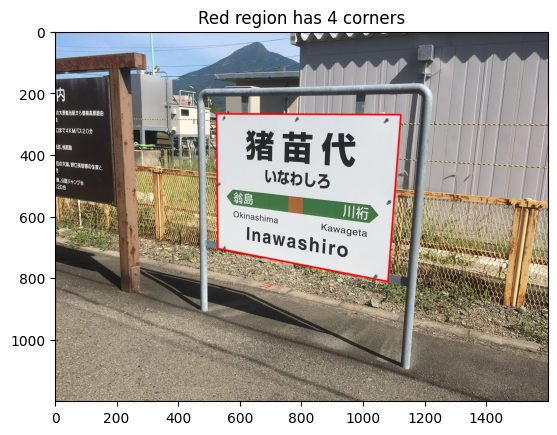
図のタイトルにあるように、今、赤色で描かれている矩形の角は 4 つであり、これで、看板に対応する四角形を取り出すことができた。

2.2.4. パースの除去

三次元の情報を二次元の写真に投影する方法はいくつかあり、その代表的なものが直投影 (orthographic projection)と透視投影 (perspective projection)である。人間の視覚は透視投影に近いとされており、カメラで写真を撮るときにも、およそ透視投影として二次元画像が得られる。

日本語のパースとは perspective のことで、美術の授業などで、一点透視や二点透視などの図法を習った人も多いだろう。透視投影は、数学的には同次座標 (homogeneous coodinates)と 4×4 の行列を用いて表わすことができる。

同次座標

同次座標とは二次元の座標を表わすのに三次元の、三次元の座標を表わすのに四次元のベクトルを使うような座標表現である。例えば、二次元座標 \(\mathbf{x} = (x, y)\)の場合であれば、四次元目に冗長次元として\(z = 1\)を付与する。このベクトルに対して 3×3 の行列を作用させることで、様々な幾何変換を行うことができる。

例えば、二次元空間上での平行移動は、単純な二次元ベクトルに 2×2 の行列を作用させるだけでは表わすことができないが、同次座標を考えることで、

\[\begin{split} \begin{bmatrix} \mathbf{I} & \mathbf{t} \\ \mathbf{0}^\top & 1 \end{bmatrix} \begin{bmatrix} \mathbf{x} \\ 1 \end{bmatrix} = \begin{bmatrix} \mathbf{x} + \mathbf{t} \\ 1 \end{bmatrix} \end{split}\]

のように表わすことができる。また、行列を作用させた結果、第 3 成分\(z\)が 1 でない値をとった時は、ベクトルを\(z\)で割り算して、第 3 成分が 1 になるように正規化する。従って、同じ座標表現においては、

\[\begin{split} \begin{bmatrix} \mathbf{x} \\ w \end{bmatrix} \equiv \begin{bmatrix} \mathbf{x} / w \\ 1 \end{bmatrix} \end{split}\]

である。この時、作用させる行列のどの部分に 0 でない値 (対角成分は 1 でない値)が入っているかによって、変換の種類を以下のように分類できる。

• 線形変換: 左上 2×2 の要素のみが有意な値を持つ

• アフィン変換: 左上 2x3 の要素のみが有意な値を持つ

• 透視投影変換: 全 3x3 の要素が有意な値を持つ

透視投影変換 (perspective transform)を表わす行列を 3x3 の成分全てが未知であるとして

\[\begin{split} \mathbf{M} = \begin{bmatrix} \mathbf{A} & \mathbf{b} \\ \mathbf{c}^\top & d \end{bmatrix} \end{split}\]

としよう。この時、変換後のベクトル\(\mathbf{x}'\)は以下のように書ける。

(2.1)\[ \mathbf{x}' = \frac{\mathbf{A}\mathbf{x} + \mathbf{b}}{\mathbf{c}^\top \mathbf{x} + d} \]

この方程式の未知数は3×3=9個で、式の数は2個である。実用的には\(d=1\)であるとして、未知数を一つ減らし、変換前後の二次元座標の組\((\mathbf{x}, \mathbf{x}')\)を4組の対応づけることで、方程式を8つ定義する。 $$

ここで察しの良い方は、(2.1)が\(\mathbf{M}\)の成分の線形式になっていないことに気づいたかもしれない。この式の右辺は未知数の分数となっているため、このままでは線形問題として解くことはできない。しかし、\(d=1\)として、右辺の分母を両辺にかけると、

\[ \mathbf{A}\mathbf{x} + \mathbf{b} - (\mathbf{x}' \mathbf{x}^\top) \mathbf{c} = 1 \]

という\(\mathbf{A}\), \(\mathbf{b}\), \(\mathbf{c}\)に関する線形式に変換することができる。あとは、この式を 4 組分集めることで、変形前後の四角形と四角形を対応付ける透視投影変換行列をを求めることができる。

---

今回の例では、看板の 4 隅の点が分かっているので、その 4 点が、長方形の点に移るような透視投影変換を求める。ただし、このままでは、長方形の縦横比が分からないので、看板の 4 隅の点の座標を元に縦横比を求めた後、高さが 1000 画素となるように変換を考える。

src_pts = approx.reshape((-1, 2)).astype("float32")

# 縦横比の計算
w = np.linalg.norm(src_pts[3] - src_pts[0])
h = np.linalg.norm(src_pts[1] - src_pts[0])
aspect = abs(w) / abs(h)

# 新しい画像サイズを設定
new_w = int(1000 * aspect)
new_h = 1000
dst_pts = np.array([(0, 0), (0, new_h), (new_w, new_h), (new_w, 0)], dtype="float32")

# 射影変換を計算して、パースをキャンセルする
warp = cv2.getPerspectiveTransform(src_pts, dst_pts)
result = cv2.warpPerspective(image, warp, (new_w, new_h))

fig, ax = plt.subplots()
ax.imshow(result)
ax.set(xticks=[], yticks=[])
plt.show()

このように、透視投影変換を考えることで、看板をあたかも正面から見たような画像を得ることができた。

問題

実写真からの図形の検出の例について、看板が白いことに着目して、二値化した時点で一番大きな白の領域を取り出すことにより、看板の領域を抽出せよ。この際、最大の白色領域を取り出した後で、その最も外側にある輪郭を、看板の輪郭線とすれば良い。

問題

直投影と透視投影の工学的な応用先の違いについて、ものの見え方、縮尺の変化の観点から説明せよ。

2.3. 参考文献

SA85

Satoshi Suzuki and Keiichi Abe. Topological structural analysis of digitized binary images by border following. Computer Vision, Graphics, and Image Processing, 29(3):396, mar 1985. doi:10.1016/0734-189x(85)90136-7.