2. カラー画像と色空間

前節「デジタル画像の表現」では、写真の各画素が赤、緑、青の三成分によって表されている、と述べた。しかし、色の表現方法には、応用的な目的に応じて様々な方法が存在する。

参考資料

• 『ディジタル画像処理 改訂第二版』 P.50 第3章 画像の性質と色空間

2.1. 色の表現

画像の色が赤、緑、青の3色を基本として表されているのは、人間の視細胞が強く反応する光の波長に関係がある。

人間の視細胞には桿体細胞 (rod cell)と 錐体細胞 (cone cell) がある。桿体細胞は光の強さを知覚する役割を持ち、錐体細胞は色を知覚する役割を持つ。このうち錐体細胞には反応する色の異なる三つの細胞があり、反応する波長の長さからL錐体、M錐体、S錐体のように呼ばれる。また、可視光の中で長波長領域は赤色、中間の波長領域は緑色、短波長領域は青色に対応することから、L, M, Sの各錐体細胞は赤錐体、緑錐体、青錐体と呼ばれることもある。

このような人間の視覚の性質に合わせて、赤、緑、青の三色で定義される色空間をRGB色空間と呼ぶ。なお、各波長の光に対するL, M, Sの各錐体細胞の反応の強さは 図 2.1 のようになっている。

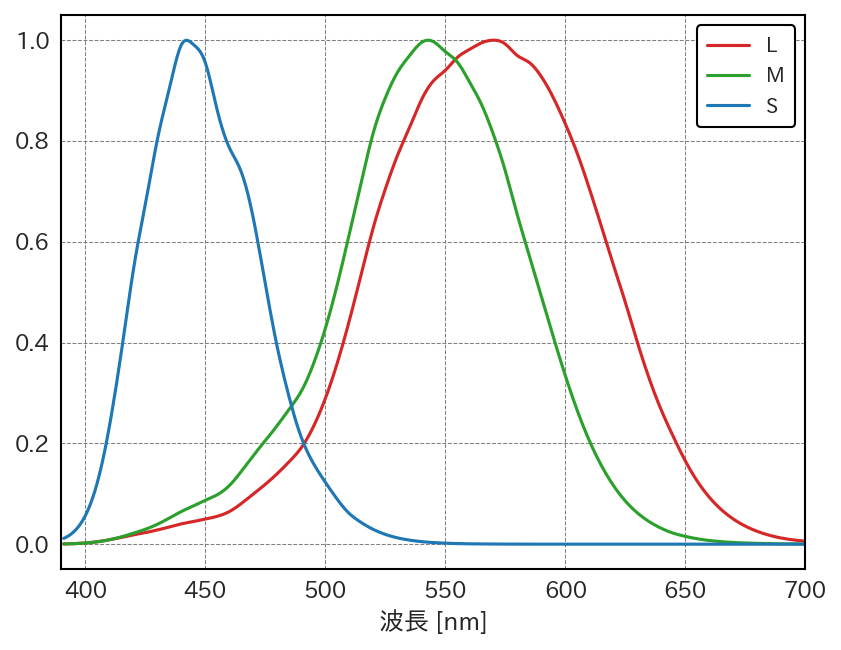
図 2.1 L, M, S錐体の各波長の光に対する反応強度

なお、ヒトは三種の色覚細胞を持つが、動物の中には二種以下の色覚細胞を持つものや3種類より多くの色覚細胞を持つ動物もいる。例えば、シャコ (mantis shrimp)は12種類もの色覚細胞を持つことが知られている (ただし、12種類の色覚で混合色を作るわけではないことが近年の研究 [4] で明らかになった)。

補足: 中心視野と周辺視野

明るさを感じる桿体細胞は網膜上で周囲領域に多く集まっており、錐体細胞は網膜の中心に多く集まっている。そのため、人間の視覚においては中心視野において色を感じやすく、周辺視野では輝度のコントラストに基づく運動情報などを感じやすい。

2.1.1. Young-Helmholtzの三色説

Youngの干渉実験でも知られる物理学者のThomas Youngは、光の波長がある程度ことなる3つの単波長光を適切に混色すると白色光と見分けがつかない光が作り出せることを発見した。同様の性質は単波長光を2つしか用いない場合には実現できず、彼は3つの光として、赤、緑、バイオレットの三色が基本色であると考えた。

その後、生理学者のHermann von Helmholtzは、人間の網膜に赤、緑、バイオレット(または青)の三色に強く反応する視細胞(今日の錐体細胞)の存在を予言した。このように、YoungとHelmholtzによって提唱された色の三原色の組み合わせによる色の表現方法をYoung-Helmholtzの三色説 (Young Helmholtz trichromatic theory)と呼ぶ。

今日でも、光の三原色として赤、緑、青の三成分が用いられている他、多くの表色系においても、性質のことなる3つの成分を用いて色を表現するのが一般的である。

2.1.2. Heringの反対色説

神経学者のHeringは、赤、緑、青 (バイオレット)の三色を基本とするYoung-Helmholtzの三色説に対して、次のようなことを考えた。

• オレンジは、赤と黄色が混ざった色に見える

• シアンは、緑と青が混ざった色に見える

• しかし、赤と緑が混ざったように見える色や青と黄色が混ざったように見える色は思いつかない

この仮定に基づき、Heringは色の表現方法として赤-緑の成分、青-黄色の成分、白-黒の成分という3つの互いに対立する色の組み合わせを用いることを提唱した。このような色の表現方法をHeringの反対色説と呼ぶ。

実際、後述する光の混色においては、赤に似た色であるマゼンタと緑の混色は無彩色になり、同様に青と黄色の混色も無彩色となる。従って、Heringの考えた「青と黄が混ざった色 (=有彩色)」というのは実際に定義しがたい色であることが分かる。

2.1.3. Munsell表色系

アメリカの画家で美術教育者のAlbert Munsellは、色を色相 (hue)、彩度 (saturation)、輝度 (brightness value)という三つの指標で表すことを提案した。この三要素で表される色空間をHSV色空間と呼ぶ。

Musellが提案したHSVの表式では、色相は円状に配置される。その中の代表的な色として、赤、黄、緑、青、紫の5色が取られ、その間を補間する色が間に配置される。このルールに基づいて円上に代表色を配置したものをMunsellの色相環と呼ぶ。

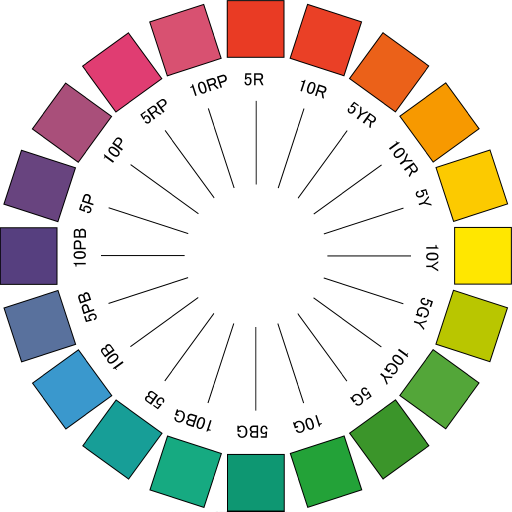
図 2.2 Munsellの色相環

Munsellの色相環は彩度と輝度の情報を追加することで三次元に拡張することもできる。輝度を高さ方向に、彩度を半径方向に取ると、Munsellの色立体と呼ばれる歪な形の立体が得られる。

図 2.3 Munsellの色立体

Munsellの色立体上では、人間が知覚可能な色のみが描かれている。人間の知覚は色ごとに感じられる輝度や色の濃さが異なるので、Munsellの色立体は 図 2.3のような歪な形となる。

2.1.4. 加法混色と減法混色

代表的には色が赤、緑、青の三成分で表されるとして、その三色で定義される空間の内部をどのように表現するかには、二通りの方法がある。例えば、読者の皆さんは、赤色と青色を混ぜると何色になると思うか、少し考えてみてほしい。

おそらく、多くの読者は「紫色」と答えたことと思う。これは答えの一つであり、もう一つの答えはピンクに近い色である「マゼンタ」である。紫色は赤色の青色の「絵の具」を混ぜたときに得られる色であり、マゼンタは赤色の光と青色の「光」を混ぜたときに得られる色である。

光は重ねるとだんだん明るくなっていくので、複数の色を混ぜると白色に近づいていく。このようなメカニズムに基づく色の混ぜ方を加法混色と呼ぶ。一方、絵の具は光の色を吸収することで、吸収されない側の色が人間の目に入ってくる。従って、絵の具を混ぜると、より多くの色が吸収されることになり、吸収されない側の色はだんだん暗く、すなわち黒に近づいていく。このようなメカニズムに基づく色の混ぜ方を減法混色と呼ぶ。

写真は、フィルムや光学素子に届く光の強さを記録したものなので、加法混色に基づく色表現を用いるのが一般的である。一方で、プリンタなどの印刷器では、インクの混色により色を表現するため、減法混色に基づく色表現を用いることが多い。

通常、プリンタのインクは黒とシアン、マゼンタ、イエローの4色で構成されている。この4色を基本とする色空間を CMYK表色系 と呼ぶ。CMYKのC, M, Yはそれぞれシアン (cyan), マゼンタ (magenta), イエロー (yellow)の頭文字であり、KはKeyの頭文字で黒に対応している。写真などのようにRGB表色系で表されているデータであっても、プリンタで印刷する際にはCMYK表色系に変換された後に、インクを用いて印刷される。

色の表現

• Young-Helmholzの三色説により三つの異なる光の混色によって白色の光と見分けがつかない光が得られることが示された

• Heringの反対色説では、光が赤-緑, 青-黄, 白-黒の3つの反対色の軸によって表せると考えた

• Muncellの表色系では、色を色相、彩度、輝度の3つの要素によって記述する

2.2. 色空間

一度、デジタル画像がRGB色空間で表現されると、そこから目的に応じて他の色空間への変換が可能となる。例えば、Munsell表色系のように色相、彩度、輝度の三成分を用いて表現される色空間にはHSV色空間やHSL色空間があり、Heringの反対色説に基づくような色空間にはYUV色空間やYCbCr色空間などがある。

しかし、デジタル画像に記録されるRGBの値は、より厳密には一体何を表しているのだろうか。人間の目に知覚される色は、物理的には波長の異なる光の組み合わせで構成されている。具体的には、光は異なる波長 \(\lambda\) ごとに異なる強度を持っており、その分布は分光強度分布 \(S(\lambda)\) で表される。

本項では、この分光強度分布 \(S(\lambda)\) を知覚色である赤、緑、青の三成分に変換する方法について見ていきたい。

2.2.1. 等色関数

色空間を理解する上で重要な考え方の一つに等色関数がある。等色関数とは、とある波長の単色光が与えられたときに、赤、緑、青の単色光をどのくらいの割合で混ぜると、人間の視覚が同じ色だと感じるかを表した関数である。人間が同じ色だと感じるようになることを動詞として等色するという。

より厳密には、赤、緑、青と述べた光は必ずしも単色光でなくとも良く、何らかの適当な光の混色であっても良い。この混色の元となる光のことを 原刺激 と呼ぶ。この原刺激にどのような色の光を使うかは色空間の定義によって異なる。

等色関数の測定実験は 図 2.4 に示すような環境で実施される。被験者は遮蔽板で区切られた二つの領域を見ており、各領域には一方に参照光、もう一方に原刺激を混色した光が当てられている。参照光を固定して、原刺激をの強さを調整したときに、被験者が同じ色だと感じたら、その光の強度を等色関数の値とする。

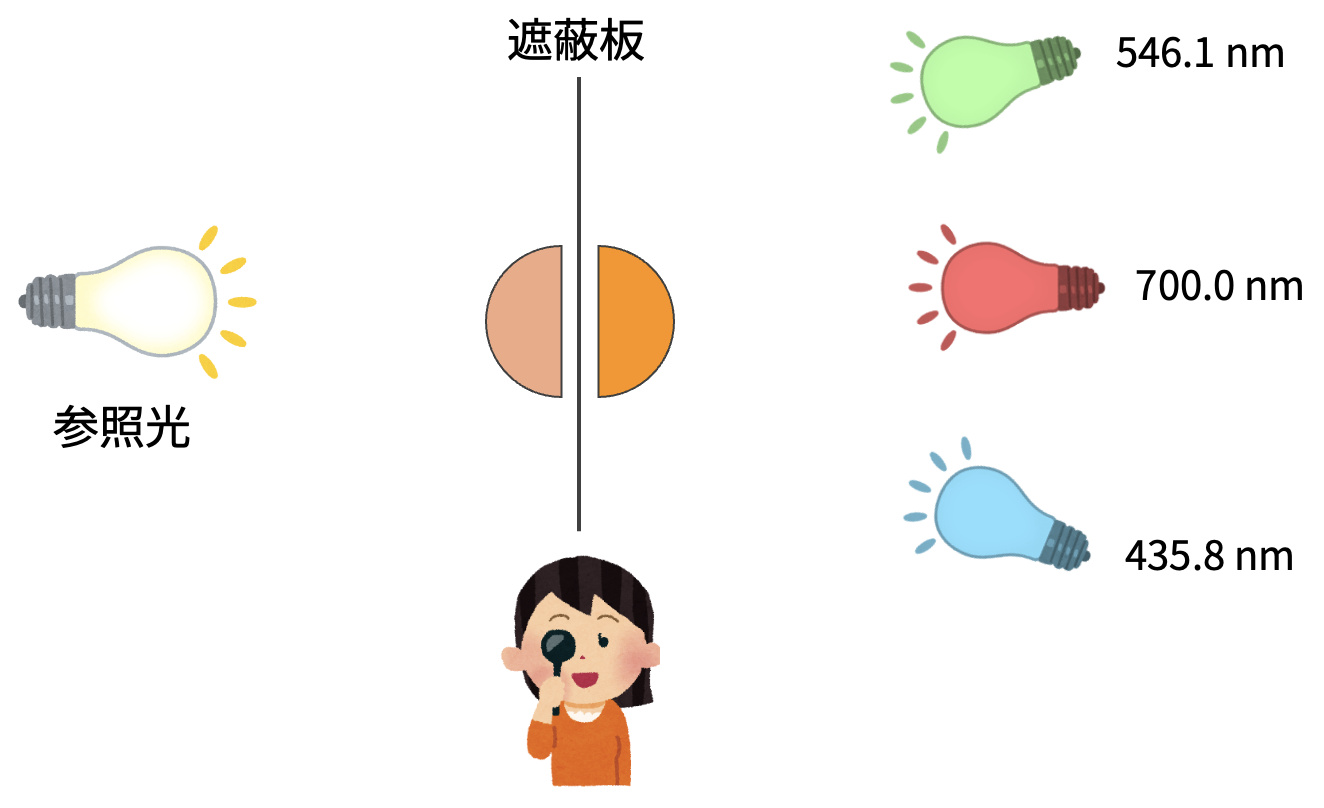
図 2.4 等色関数の測定実験

CIE 1931 RGB表色系 (以後、CIE RGB表色系)では、原刺激として波長が700nm、546.1nm、435.8nmの三種類の単色光を用いて測定が行われた。CIE RGB表色系の等色関数を 図 2.5 に示す。このグラフは、参照光の波長 \(\lambda\) が横軸に取られている。

赤、緑、青の原刺激に対応する \(\bar{r}(\lambda)\), \(\bar{g}(\lambda)\), \(\bar{b}(\lambda)\) の値は、可視光の範囲で積分したときに同じ値になるように正規化されている。すなわち以下の式が満たされる。

(2.1)\[ \int_0^\infty \bar{r}(\lambda) \mathrm{d} \lambda = \int_0^\infty \bar{g}(\lambda) \mathrm{d} \lambda = \int_0^\infty \bar{b}(\lambda) \mathrm{d} \lambda \]

実際に参照光と同じ色を得るためには、輝度の比として 1 : 4.5907 : 0.0601 の強さを持つ単色光を用意し、その光の強度を \(\bar{r}(\lambda)\), \(\bar{g}(\lambda)\), \(\bar{b}(\lambda)\) に設定して混色すれば良い。

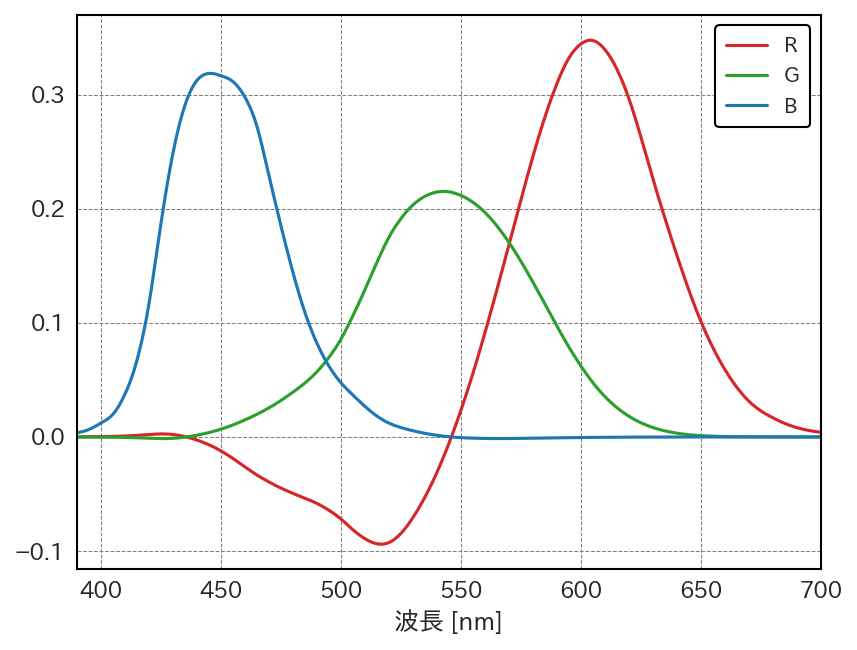
図 2.5 CIE RGB表色系の等色関数

図 2.5 をよく見てみると、 \(\bar{r}(\lambda)\) の値が一部の波長で負の値を取っていることが分かる。図 2.4では、一方に参照光、他方に原刺激が当てられていたが、負の値の意味するところは、とある原刺激を参照光側に移動して混色することを意味する。520nm付近の \(\bar{r}(\lambda)\), \(\bar{g}(\lambda)\), \(\bar{b}(\lambda)\) の値を例に取ると、参照光と赤色の原刺激を混色したものが、緑色と青色の原刺激を混色したものと等色したことを意味する。

またCIE RGB表色系の等色関数からはいくつかの色の性質が読み取れる。分かりやすいところでは、原刺激に対応する波長、すなわち 700nm, 546.1nm, 435.8nmの箇所では、原刺激の1つが非零の値を、その2つの原刺激は0を取っている。

また、原刺激の波長に対応する箇所以外では、3つの原刺激の強さの少なくとも一つは負の値を取っている。参照光として用いられる光は単色光であり、この光は彩度が最大であると考えられる。一方で、加法混色の場合には光を混色すると彩度が下がる方向に向かう。したがって、必ず負の値が現れる、ということは、原色に対応する単色光の色はいかなる原刺激の混色でも表せないことを意味している。

2.2.2. Grassmannの法則

とある単色光 \(C_1\)と等色する原刺激の強さが \((R_1, G_1, B_1)\)であるとする。また、別の単色光 \(C_2\)と等色する原刺激の強さは \((R_2, G_2, B_2)\)であるとする。このとき、\(C_1\) と \(C_2\)を混色して得られる色 \(C_3\) と等色する原刺激の強さは \((R_1 + R_2, G_1 + G_2, B_1 + B_2)\) となる。この法則を Grassmannの法則 と呼ぶ。

この法則を用いると任意の分光分布 \(S(\lambda)\) を持つ光を表すのに必要な原刺激の強度 \(R\), \(G\), \(B\)は次のように表せる。

\[\begin{split} \begin{align*} R = \int_0^{\infty} S(\lambda) \bar{r}(\lambda) \mathrm{d} \lambda \\ G = \int_0^{\infty} S(\lambda) \bar{g}(\lambda) \mathrm{d} \lambda \\ B = \int_0^{\infty} S(\lambda) \bar{b}(\lambda) \mathrm{d} \lambda \end{align*} \end{split}\]

この結果は、人間が知覚できる任意の色が、たとえ物理的に異なる分光分布を持っていたとしても、\(R\), \(G\), \(B\)の三成分によって記述できることを意味している。

2.2.3. CIE XYZ表色系

CIE RGB表色系は部分的に負の値を取るため、扱いが複雑になることがある。そこで、CIE XYZ表色系はCIE RGB表色系の原刺激の値を線形変換することで、等色関数が可視光範囲内で非負の値をとるように定義している。

CIE XYZ表色系で用いられる原刺激は実際に存在する光ではなく、仮想的な光で、それぞれの等色関数を \(\bar{x}(\lambda)\), \(\bar{y}(\lambda)\), \(\bar{z}(\lambda)\) のように表す。この際、 \(\bar{y}(\lambda)\) は、錐体細胞の明るさ感度関数 \(V(\lambda)\) と同じになるように定義される。CIE XYZ表色系の等色関数は 図 2.6 のようになる。

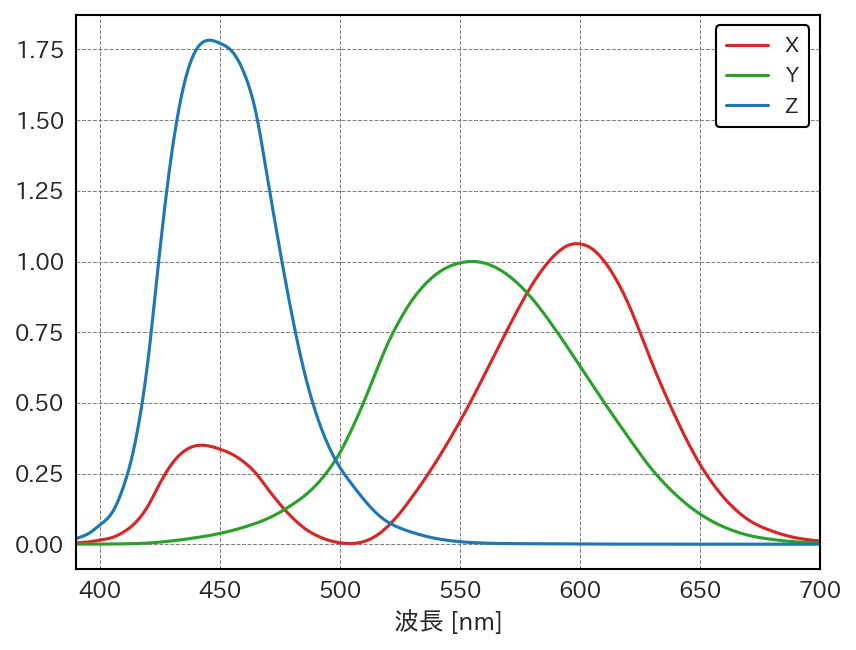
図 2.6 CIE XYZ表色系の等色関数

CIE XYZ表色系で表された色の3要素 \((X, Y, Z)\) はCIE RGB表色系で表された色の3要素 \((R, G, B)\) から求められる。

(2.2)\[\begin{split} \begin{align*} \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} &= \frac{1}{0.17697} \begin{pmatrix} 0.49000 & 0.31000 & 0.20000 \\ 0.17697 & 0.81240 & 0.01063 \\ 0.00000 & 0.01000 & 0.99000 \end{pmatrix} \begin{pmatrix} R \\ G \\ B \end{pmatrix} \\ &= \begin{pmatrix} 2.7688 & 1.7517 & 1.1301 \\ 1.0000 & 4.5906 & 0.0601 \\ 0.0000 & 0.0575 & 5.5942 \end{pmatrix} \begin{pmatrix} R \\ G \\ B \end{pmatrix} \end{align*} \end{split}\]

(2.2)に現れる行列の係数はどこからやってきたのだろうか。この変換の意味を少し考えてみたい。

(2.2)の1行目に現れる \(3 \times 3\) の係数行列は横に要素を足し上げるとすべての行で1となるように値が設定されている。これは、 (2.1)に示したような性質を \(\bar{x}(\lambda)\), \(\bar{y}(\lambda)\), \(\bar{z}(\lambda)\)にも持たせるためのもので、実際、これらの等色関数は次の等式を満たす。

(2.3)\[ \int_0^\infty \bar{x}(\lambda) \mathrm{d} \lambda = \int_0^\infty \bar{y}(\lambda) \mathrm{d} \lambda = \int_0^\infty \bar{z}(\lambda) \mathrm{d} \lambda \]

また、(2.2)の2行目に現れる \(3 \times 3\) の係数行列の2行目の3つの係数は、CIE RGB表色系の計測実験に用いられた原刺激の強さに基づくことが確認できる。

これに加えて、XYZ表色系において、

\[ x = \frac{X}{X + Y + Z}, \quad y = \frac{Y}{X + Y + Z} \]

のように\(x\), \(y\)を定義して、xy平面上に色をプロットしたものを色度図と呼ぶ。CIE XYZ色空間はCIE 1931 xy色度図に示すように、可視光が色度図上で \((0, 0)\), \((0, 1)\), \((1, 0)\)の三角形の内側に収まるように定義されている。

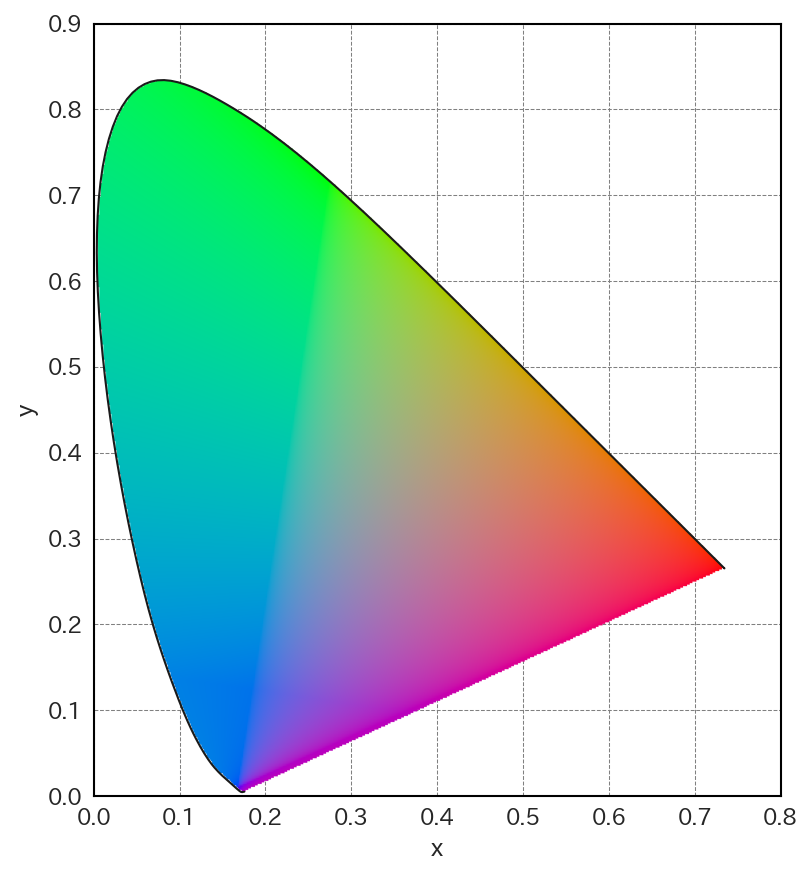
図 2.7 CIE 1931 xy色度図

2.2.4. CIE L^*a^*b^*表色系

CIE 1976 L^*a^*b^*表色系 (以後、簡単のためにCIE Lab表色系)は、CIE XYZ表色系を基にして、 色覚的均一性 を持つように定義された色空間である。色覚的均一性とは、任意の2つの色が与えられたときにLab色空間上での距離が人間の感じる色の違いに比例するような性質を指す。

CIE Lab表色系による色表現はCIE XYZ表色系の3要素 \((X, Y, Z)\) から次のように計算できる。

(2.4)\[\begin{split} \begin{align*} L^{*} &= 116 f(Y / Y_n) - 16 \\ a^{*} &= 500 (f(X / X_n) - f(Y / Y_n)) \\ b^{*} &= 200 (f(Y / Y_n) - f(Z / Z_n)) \end{align*} \end{split}\]

ただし、 \(X_n\), \(Y_n\), \(Z_n\)は参照白色点の値を表す。例えば、D65と呼ばれる参照白色点の場合には、\(X_n = 95.047\), \(Y_n = 100\), \(Z_n = 108.883\)となる (ただしY = 100として正規化した場合)。また、関数\(f\)は次のように定義される。

\[\begin{split} f(t) = \begin{cases} t^{1/3} & (t > \delta) \\ \frac{t}{3 \delta^2} + \frac{4}{9} & (t \leq \delta) \end{cases} \end{split}\]

CIE Lab表色系において、L^*は0から100の値を取り、a^*ならびにb^*はおおむね-1から1の間の値を取る。

2.3. デジタルカラー画像

ここまで、画像の色表現に用いられる色表現について見てきたが、ここからは、どのようにしてデジタルカラー画像を取得し、表示するのかについて見ていきたい。

2.3.1. カラー画像の取得

前節 デジタル画像の表現 ではCCDあるいはCMOSをイメージセンサとして用いることで光の強さをデジタルデータとして記録できることを述べた。しかし、ここまでの説明から分かる通り、色を表現するには赤、緑、青といった3つ以上の基本色が必要であるため、光の強さを記録できるだけでは不十分である。

一般的なデジタルカメラは、CCDやCMOSのセンサが並んだセンサアレイ上にBayerフィルタと呼ばれる色フィルタが備え付けられており、各イメージセンサは赤、緑、青のいずれかの色フィルタを通した光の強度を観測する。この際、人間の視覚系が緑の光に対して相対的に高い感度を持つことから、Bayerフィルタ上は赤、緑、青に対するイメージセンサの数の比が1 : 2 : 1になるように設計されている。

Bayerフィルタを用いる場合、カメラから直接得られる画像は各画素が赤、緑、青のいずれかの値しか持っていない。このような画像をモザイク画像と呼ぶ。したがって、全画素が色を持つようなカラー画像を得るためには事後的な画像処理が必要である。このようなモザイク画像からカラー画像への変換処理を デモザイキング (demosaicing)と呼ぶ。

モザイク画像	デモザイキング後

デモザイキングには非常に多数のアルゴリズムが提案されている[5]が、最もシンプルなアルゴリズムは、モザイク画像の各色の情報を、有効値を持つ隣接画素の値の平均によって求めるバイリニア補間である。

上記のモザイク画像は赤、緑、青の成分が次の条件を満たす画素で有効値を持つ (x座標, y座標ともに0から始まる整数)。

• 赤成分: x座標が奇数かつy座標が偶数

• 緑成分: x座標とy座標がともに偶数あるいはともに奇数 (x座標とy座標の和が偶数)

• 青成分: x座標が偶数かつy座標が奇数

以下の図に示す通り、赤と青の成分を補間する場合には隣接する有効画素が2つの場合と4つの場合が存在する。一方、緑成分を補間する場合、隣接する有効画素はいずれも4つ存在する。

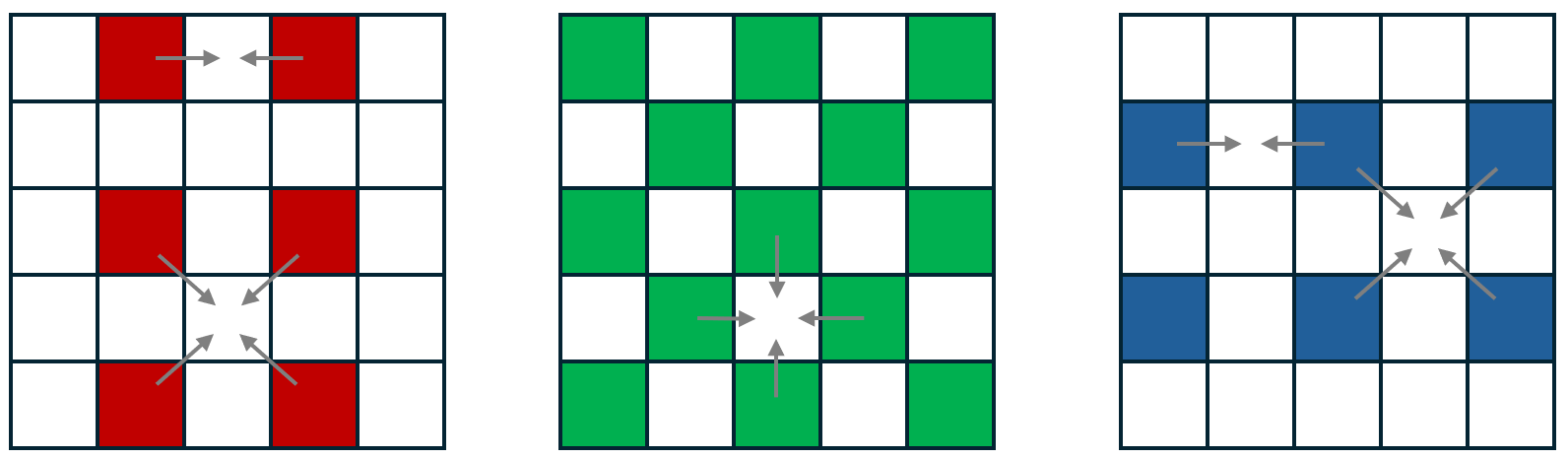
図 2.8 赤、緑、青の各成分に対するデモザイキングの例

ただし、バイリニア補間のように空間的に近い位置の画素を全て平均してしまうと、エッジのような輝度の変化を持つ部分で色がぼやけてしまい、結果として、エッジ付近に偽色 (false color)と呼ばれる色のにじみやジッパー効果 (zipper effect)と呼ばれるゴマ粒上のアーティファクトが発生してしまう [6]。

このような問題を防ぐ手法の一つに エッジセンシング手法 と呼ばれる手法がある。エッジセンシング手法では、周囲の有効値を持つ画素の情報を用いて、x方向ならびにy方向のエッジ強度を最初に求め、各方向のエッジ強度の大小関係を用いて色の補間に用いる有効画素を選択する。

練習問題

隣接画素値の平均に基づくデモザイキングのプログラムを作成し、上記のモザイク画像に対して、その効果を検証せよ。

2.3.2. カラー画像の表示

カラー画像をディスプレイに表示したり、プリンタを用いて印刷物にする場合、各デバイスが表現できる色には物理的な制約がある。従って、異なるディスプレイや異なるプリンタで表現される色は必ずしも同じではない。このようなデバイスに依存する色表現を デバイス依存色 と呼ぶ。

当然ながら、CIE RGB表色系やCIE XYZ表色系は色の定義が物理的な分光分布と等色関数によって定義されるためデバイスに依存しない色表現である。このような色表現を デバイス独立色 と呼ぶ。

デバイス独立色には多くのものが存在するが、ディスプレイやプリンタなどで表現できる色域は、sRGB色空間やAdobe RGB色空間などで定義されている。これらのデバイスのほとんどはsRGB色空間で表せる色域全体を表現できるように作られているため、その範囲内であればデバイスが変わっても同じ色を表示したり印刷したりできる。一方で、Adobe RGB色空間はsRGB色空間よりも広い色域を持つものの、全てのデバイスでその広い色域が表現できるわけではないので注意が必要である。

sRGBで定義された色は、適当な変換を行うことでCIE XYZ表色系やCIE Lab表色系などで表すことができる。CIE XYZ表色系はデバイス独立色であるので、一定の変換により得られるsRGBも当然デバイス独立色である。

ガンマ補正

ガンマ補正 はディスプレイや印刷物など人間が目にする媒体に色を表示する際に、色の明るさを調整するために用いられる。

ここまでに紹介したCIE RGB表色系やCIE XYZ表色系は、等色関数を用いて物理的な光の強さに比例するような値を成分として持っている。しかし、人間が光の明るさを知覚する場合には、物理的な光の強さが2倍になったからといって、2倍明るく感じるわけではない。

実際、人間の視覚は暗い光の変化には敏感で、逆に明るい光の変化にはそれほど敏感でない。そこで、光の強さが弱い (=暗い)場合には範囲を広く、光の強さが強い(=明るい)場合には範囲を狭くするような非線形変換を施して色の明るさを調整する。

ガンマ補正にはガンマ値と呼ばれるパラメータ\(\gamma\)があり、多くの場合は \(\gamma = 2.2\)が用いられる。ガンマ補正の式は単純には次のように表される。

(2.5)\[ I_{\text{out}} = I_{\text{in}}^{\frac{1}{\gamma}} \]

ただし、 \(I_{\text{in}}\) は入力の強度、 \(I_{\text{out}}\) は出力の強度でそれぞれ0から1の範囲の値を取るものとする。

なお、上記のガンマ補正の式をそのまま用いると、 \(I_{\text{in}}\) の値が小さいときに数値計算上の誤差が大きくなるという問題がある。そこで\(\gamma = 2.2\)とする代わりに、暗い色は線形に変換し、明るい色はガンマ値を\(\gamma = 2.4\)として変換するような変換が行われる。

(2.6)\[\begin{split} I_{\mathrm{out}} = \begin{cases} 12.92 I_{\mathrm{in}} & (I_{\mathrm{in}} < 0.0031308) \\ 1.055 I_{\mathrm{in}}^{1 / 2.4} - 0.055 & (I_{\mathrm{in}} \geq 0.0031308) \end{cases} \end{split}\]

こうすると、低輝度の領域は単純な線形変換であるために、数値誤差の影響を受けづらくなる。

練習問題

ガンマ補正に用いられる (2.6) と (2.5) の違いを0-1の範囲でプロットし、その違いを確認せよ。

sRGBからCIE XYZへの変換

sRGBからCIE XYZへの変換は次のように行う。sRGBの値は通常0から255の間の整数値ないし、0から1の間の実数値で表されている。ここでは、0から255の整数値で表されている場合にはあらかじめ255で除しておき、0から1の間の実数値に変換してから以下の操作を行う。

まず、sRGBの値を逆ガンマ補正によりLinear RGBと呼ばれる値に変換する。

\[\begin{split} C_{\text{linear}} = \begin{cases} \frac{C_{\text{sRGB}}}{12.92} & (C_{\text{sRGB}} \leq 0.04045) \\ \left( \frac{C_{\text{sRGB}} + 0.055}{1.055} \right)^{2.4} & (C_{\text{sRGB}} > 0.04045) \end{cases} \end{split}\]

ここで、\(C_{\text{sRGB}}\)はsRGBの各成分の値、\(C_{\text{linear}}\)はLinear RGBの各成分の値を表す。次に、Linear RGBからCIE XYZへの変換を行う。

\[\begin{split} \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} = \begin{pmatrix} 0.4124 & 0.3576 & 0.1805 \\ 0.2126 & 0.7152 & 0.0722 \\ 0.0193 & 0.1192 & 0.9505 \end{pmatrix} \begin{pmatrix} R_{\text{linear}} \\ G_{\text{linear}} \\ B_{\text{linear}} \end{pmatrix} \end{split}\]

ただし、Linear RGBからCIE XYZへの変換に用いる行列は「白色がどの色か」によって異なる。上記の例はD65と呼ばれる白色点を用いた場合の変換行列であるので注意すること。

CIE XYZからsRGBへの変換

CIE XYZからsRGBへの変換は、sRGBからCIE XYZへの変換の逆変換を行う。まず、CIE XYZからLinear RGBへの変換を行う。

\[\begin{split} \begin{pmatrix} R_{\text{linear}} \\ G_{\text{linear}} \\ B_{\text{linear}} \end{pmatrix} = \begin{pmatrix} 3.2406 & -1.5372 & -0.4986 \\ -0.9689 & 1.8758 & 0.0415 \\ 0.0557 & -0.2040 & 1.0570 \end{pmatrix} \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} \end{split}\]

先ほどと同様、上記の行列もD65を白色点として用いた場合の行列であることに注意すること。次に、ガンマ補正により、Linear RGBからsRGBへの変換を行う。

\[\begin{split} C_{\text{sRGB}} = \begin{cases} 12.92 C_{\text{linear}} & (C_{\text{linear}} \leq 0.0031308) \\ 1.055 C_{\text{linear}}^{1/2.4} - 0.055 & (C_{\text{linear}} > 0.0031308) \end{cases} \end{split}\]

練習問題

Matplotlibには viridisやinfernoといった知覚的に均一なカラーマップがいくつか用意されている (参考)。このカラーマップ上の値を取得し、CIE Lab色空間上において、各色がおよそ等間隔に並んでいることを確認せよ。

なお、カラーマップからRGBで表された色を取り出すには次のようにすれば良く、ここで得られる数値がsRGBの値であるとしてプログラムを作成せよ。

import numpy as np
from matplotlib import cm

vals = np.linspace(0.0, 1.0, 256)
cmap = cm.viridis(vals)[:, :3]

2.3.3. ダイナミックレンジ

前述の通り、各画素に記録された色情報は有限のビット深度を持っている。従って、画像の中で表現できる色、あるいは光の暗さ・明るさには制限がある。このような表現 (知覚・表示)できる明るさの範囲のことを ダイナミックレンジ (dynamic range)と呼ぶ。

実は、人間の視覚にも一度に知覚できる光の強度には一定の幅がある。そのため、暗い部屋から明るい場所に出たときに、しばらく周囲が眩しく感じることがある。この際、人間の視覚では周囲の明るい状況に応じて知覚できる光の強度範囲を変化させる明順応が起こっている (逆に暗い環境に合わせて知覚を調整する機能を暗順応と呼ぶ)。

デジタル画像上で高いダイナミックレンジを持つ画像を表すには、より多くのビットを色の記録に用いる必要があり、デジタルカメラで撮影できるいわゆる RAW画像 は14ビット前後のビット深度 (カメラの機種により異なる)を持っており、JPEG等の8ビット深度の画像よりも広いダイナミックレンジを持っている。そのため、RAW画像を撮影後に編集することで、人間の暗順応や明順応の要領で、8ビット深度のJPG画像にどの範囲の明るさを残すかを決めることもできる。

輝度が8ビット深度で表される画像を 低ダイナミックレンジ画像 (low-dynamic-range image, LDR)と呼び、反対に8ビットより大きなビット深度を持つ画像を 高ダイナミックレンジ画像 (high-dynamic-range image, HDR)と呼ぶ。

HDR画像合成

狭いダイナミックレンジしか持たないLDR画像を取り出す明るさを変えながら複数枚撮影し、それらの画像を合成することで事後的にHDR画像を作り出す技術がある。この技術を HDR画像合成 (HDR imaging)と呼ばれ、現在はスマートフォンなどにも搭載されている機能である。

スマートフォンを用いて写真を撮影しているとそれほど意識することはないが、写真の明るさは、絞りをどれくらい開いているか、シャッターをどのくらいの時間開けているか、などの複数の要因によって決まる。HDR画像合成を行う場合には、シャッターを開けている時間を変えながら撮影することが多い。

HDR画像合成の技術は、1998年にPaul Devebecらによって提案されたもので、ビット深度がいくつであっても、露出を変更しながら複数の画像を撮影することでダイナミックレンジを持つ画像が撮影できる可能性を示した [7]。この技術は、コンピュータ・グラフィクスにおいて画像を光源の代わりに用いる環境マップを作成するうえで大変重要である。

反対に高いダイナミックレンジを持つ画像を見た目の情報をなるべく保持するようにLDR画像に変換する技術も非常によく研究されている。このような技術は トーンマッピング (tone mapping)と呼ばれており、代表的なものにはReinhardらが2002年に提案した手法[8]やFattalらが2002年に提案した手法[9]などがある。

図 2.9 HDR画像合成の例。右側の合成結果はトーンマップ済みの画像 (画像出典)