4. 画像の幾何変換

本節では、画像の平行移動、回転の他、アフィン変換、射影変換などによる画像の変形について解説する。画像の幾何変換には、画像の再サンプリングが必要になるが、この時に重要になるのが デジタル画像の表現 でも述べた標本化定理である。本設では、標本化定理の簡単な証明にも触れ、なぜエイリアシングの発生原因にも言及する。

参考資料

• 『ディジタル画像処理 改定第二版』 P.172 第8章 幾何学的変換

4.1. 同次座標系

画像の幾何変換について説明するための道具として、まず 同次座標系 (homogeneous coordinates) について説明する。

画像の各画素は、それぞれの位置を表す二次元座標を持っていると考えられる。一例として、画像を角度 \(\theta\) だけ回転させる場合を考えてみると、回転後のとある画素の位置 \((x', y')\) は、その画素の元の位置 \((x, y)\) に対して回転行列 \(\mathbf{R}\) を掛けることで求められる。

\[\begin{split} \begin{pmatrix} x' \\ y' \end{pmatrix} = \mathbf{R} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \end{split}\]

この変換に対して、さらに移動量のベクトルを \(\mathbf{t}\) とする平行移動が加わったとすると、移動後の位置は次のように表せる。

(4.1)\[\begin{split} \begin{pmatrix} x' \\ y' \end{pmatrix} = \mathbf{R} \begin{pmatrix} x \\ y \end{pmatrix} + \mathbf{t} = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} t_x \\ t_y \end{pmatrix} \end{split}\]

この \((x', y')\) の表現は元の位置 \((x, y)\) に対して、行列との積、ベクトルとの和という二つの演算を行う必要がある。同次座標系の目的は、このような座標変換を1つの変換行列によって表すことである。

同次座標系では、二次元座標を冗長次元を1つ加えて、三次元ベクトルとして表す。ただし、実際の二次元座標を取り出すときには、冗長次元の値が1になるように正規化する。すなわち、同次座標系における三次元ベクトル \((x, y, z)\) に対応する二次元座標は \((x / z, y / z)\) である。

とある二次元座標 \((x, y)\) に対して、同次座標系を用いた座標変換を行う場合、三次元ベクトル \((x, y, 1)\) を用意し、\(2 \times 3\) あるいは、\(3 \times 3\) の行列を作用させる。 (4.1) の式を同次座標系で扱うと、次のように書き直せる。

(4.2)\[\begin{split} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} \cos \theta & -\sin \theta & t_x \\ \sin \theta & \cos \theta & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{split}\]

この式から分かる通り、同次座標系を用いると、並進を含む座標変換であっても、行列を掛けるだけで表現できる。また、同次座標系を用いると、二次元空間における行列積やベクトル和だけでは表せない「せん断」 (shear)や「射影変換」 (perspective transformation) などの変換を表すことができる。

4.1.1. 同次座標系を用いた変換の意味

ここまでの説明で、二次元平面上の図形の変換を考える際に同次座標系を用いると、表せる変換の幅が広がることは理解してもらえたと思う。しかし、同次座標系を用いた変換で何が起こっているのかを直感的に理解するのは少々難しい。

イメージとして同次座標系を用いた変換を理解するために、まずは次の図を見てほしい。

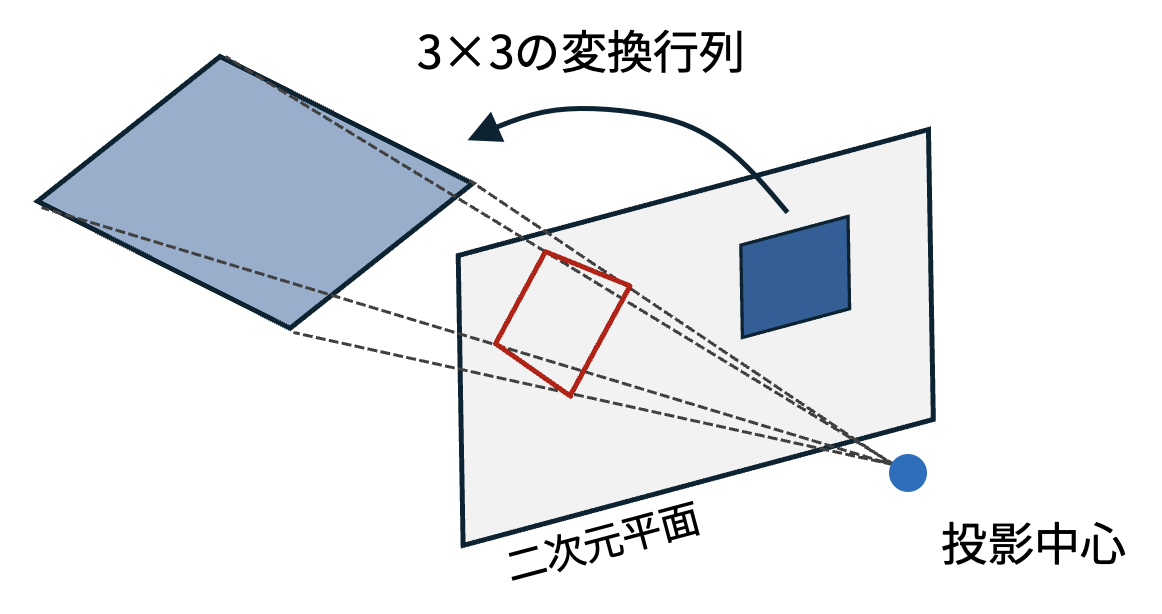
図 4.1 同次座標系を用いた幾何変換のイメージ

本図は三次元空間上に投影中心と書かれた点が原点であり、その投影中心から z軸方向に距離1だけ離れた場所に図形が描かれるべき二次元平面が位置している。 従って、二次元平面上の点の三次元位置は常に \((x, y, 1)\) のように書ける。

この三次元座標を \(3 \times 3\) の行列で変換することを考えよう。三次元空間において \(3 \times 3\) の行列を用いる変換は、二次元空間において \(2 \times 2\) の行列を用いる変換と同様に平行移動などは表せず、回転や拡大・縮小といった一部の変換だけを表現できる。

三次元空間内で、二次元平面上に描かれた図形を回転したり拡大・縮小したりすると、当然、平面から外れた位置に図形が移動する。その平面から外れた図形を二次元平面に再投影することで得られる図形が、同次座標系を用いた変換の結果なのである。この際、投影中心が原点であることを考えれば、この投影操作がz座標によるx, y両座標の割り算で実現できることは容易に理解できるだろう。

このように、同次座標系を用いた二次元図形の変換は、原点から一定の距離にある平面上の図形を、三次元空間内で線形変換した結果なのである。

4.1.2. アフィン変換

アフィン変換 (affine transformation)とは、同次座標系に対して \(2 \times 3\) の行列を掛けることで表現できる変換のことを指す。アフィン変換を用いると平行移動、回転、拡大・縮小などの変換を表すことができる。

アフィン変換を用いる場合、変換前の座標は \((x, y, 1)\) のように同次座標系で表され、変換後の二次元位置は \((x', y')\) のように通常の二次元座標系で表される。

\[\begin{split} \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{split}\]

言うまでもなく、 (4.2) に示した回転と並進を含む座標変換はアフィン変換で表せる。

アフィン変換の重要な性質に群構造がある。とある変換が群構造をなす、というのは、合成変換を表す作用素を \(\otimes\) のように定義したときに、変換が次の性質を満たすことを言う。

• 単位元としての恒等変換が存在する。

• 任意の変換に対して逆変換が存在する。

• 変換の合成が作用素 \(\otimes\) 対して閉じている。

この事実は、アフィン変換を表す \(2 \times 3\) の行列に行を追加して (4.2) のような \(3 \times 3\) の行列として表すと簡単に理解できる。この場合、アフィン変換 \(\mathcal{T}\) は、\(2 \times 2\) の行列 \(\mathbf{A}\) と \(2\) 次元ベクトル \(\mathbf{b}\) を用いて次のように表せる。

\[\begin{split} \mathcal{T} = \begin{pmatrix} \mathbf{A} & \mathbf{b} \\ \mathbf{0} & 1 \end{pmatrix} \end{split}\]

このアフィン変換 \(\mathcal{T}\) は、 \(\mathbf{A}\) が単位行列、 \(\mathbf{b}\) がゼロベクトルのとき恒等変換を表す。また、 \(\mathbf{A}\) が正則行列、すなわち逆行列を持つ行列である時、 \(\mathcal{T}\) の逆変換 \(\mathcal{T}^{-1}\) は次のように表せる。

\[\begin{split} \mathcal{T}^{-1} = \begin{pmatrix} \mathbf{A}^{-1} & -\mathbf{A}^{-1} \mathbf{b} \\ \mathbf{0} & 1 \end{pmatrix} \end{split}\]

最後に、二つのアフィン変換 \(\mathcal{T}_1\) と \(\mathcal{T}_2\) の合成変換は次のようなアフィン変換で表せる。

\[\begin{split} \mathcal{T}_1 \otimes \mathcal{T}_2 = \begin{pmatrix} \mathbf{A}_1 \mathbf{A}_2 & \mathbf{A}_1 \mathbf{b}_2 + \mathbf{b}_1 \\ \mathbf{0} & 1 \end{pmatrix} \end{split}\]

以上のことから、アフィン変換が群構造を持つことが確認できた。このようなアフィン変換を元とする群を特に アフィン群 と呼ぶ。

4.1.3. 射影変換

二次元座標系において、四角形を構成する4点を別の四角形の4点に移すような変換を考えたい。同次座標系を用いる場合、1対の点の対応関係は以下の式で表されるのだった。

\[\begin{split} \begin{pmatrix} x' \\ y' \\ z' \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{split}\]

この連立方程式において変換後の座標は \((x' / z', y' / z')\) であるので、変換後の座標 \((X, Y)\) は次のように表せる。

(4.3)\[\begin{split} \begin{align*} X &= \frac{a_{11} x + a_{12} y + a_{13}}{a_{31} x + a_{32} y + a_{33}} \\ Y &= \frac{a_{21} x + a_{22} y + a_{23}}{a_{31} x + a_{32} y + a_{33}} \end{align*} \end{split}\]

今求めたいのは変換行列の成分 \(a_{ij}\) であるので、これらの成分に関する線形式に変換すると、次の二式が得られる。

\[\begin{split} \begin{align*} a_{31} x X + a_{32} y X + a_{33} X &= a_{11} x + a_{12} y + a_{13} \\ a_{31} x Y + a_{32} y Y + a_{33} Y &= a_{21} x + a_{22} y + a_{23} \end{align*} \end{split}\]

四角形の4点に対して同様の式を考えると、制約式として線形式が4つ得られる。一方、一般的な同次座標系における変換は未知数が9つであるので、自由度が1余ってしまう。

ここで (4.3) に注目すると、座標変換後の結果 \((X, Y)\) の値を求めるにあたっては、右辺の分数の分母と分子の両方を \(a_{33}\) で割ったとしても結果が変わらないことが分かる。そこで、新たに \(a'_{ij} = a_{ij} / a_{33}\) と置き換えると、次のような式が得られる。

\[\begin{split} \begin{align*} X &= \frac{a'_{11} x + a'_{12} y + a'_{13}}{a'_{31} x + a'_{32} y + 1} \\ Y &= \frac{a'_{21} x + a'_{22} y + a'_{23}}{a'_{31} x + a'_{32} y + 1} \end{align*} \end{split}\]

このようにすると、求めるべき係数から \(a_{33}\) が減り、合計8個になる。故に、四角形の4点の対応関係によって与えられる制約式8個から全ての係数 \(a'_{ij}\) を決定することができる。結果として、求めるべき変換は次のような行列になる。

\[\begin{split} \mathbf{H} = \begin{pmatrix} a'_{11} & a'_{12} & a'_{13} \\ a'_{21} & a'_{22} & a'_{23} \\ a'_{31} & a'_{32} & 1 \end{pmatrix} \end{split}\]

このような任意の四角形を別の任意の四角形に移すような変換を 射影変換 と呼ぶ。

4.2. 画像の再サンプリング

ここまで、二次元座標系における同次座標系を用いた座標変換について見てきた。ここからは、矩形領域に定義された画像を幾何変換して、別の二次元平面上の(必ずしも長方形でない)四角形の上に再配置する方法について見ていこう。

安直に考えると、変換元の画像の各画素について、その画素の位置を幾何変換して得られる変換後の画像上の位置を求めて、その位置に対応する画素に変換元の画像と同じ色を塗れば良さそうだ。しかし、このやり方にはいくつか問題がある。

単純な画像の拡大を例にとって考えてみると、拡大された画像のすべての画素は、何らかの有意な色情報を持っているべきだが、上記のやり方を用いると、拡大後の画像上で拡大前の画像の画素の数分だけしか、画素が塗りつぶされず、歯抜けのような画像になってしまう。

反対に、画像を縮小する場合を考えてみると、縮小前の画像の異なる2つの画素が、縮小後の画像の同じ画素と対応することも起こり得る。もちろん、そのような場合には、同じ画素に対応する複数の画素の平均などを取れば良いのだろうが、縮小後の各画素について対応する縮小前の画素の画素値を保持する必要があり、あまりスマートなやり方とは言えない。

そこで、画像の幾何変換を行う場合には、元の画像の画素の位置を幾何変換するのではなく、 変換結果の画像の画素を逆変換することで元画像の画素と対応付ける。こうすれば、変換後の画像の画素について、変換前の画像の内側の領域に対応する画素については、常に何らかの色情報を割り当てることができる。

ただし、逆変換によって得られる変換前の画像上の対応位置は整数値の座標になるとは限らないので、実数値の座標に対して、どのように色情報を割り当てるかを考える必要がある。この操作のことを 再サンプリング (resampling) と呼ぶ。

4.2.1. 再サンプリングの方法

再サンプリングの方法にはいくつのかの方法があるが、ここでは、代表的な3つの方法を紹介する。

• 最近傍補間 (nearest-neighbor interpolation)

• バイリニア補間 (bilinear interpolation)

• バイキュービック補間 (bicubic interpolation)

これらの方法は、一般的な画像の幾何変換に用いることができるが、画像の「縮小」を行う場合に限っては、インターエリア法 (inter-area method)と呼ばれる方法を用いる場合もある。この理由については後述する。

最近傍補間

変換後の画像上の位置 \(\bar{\mathbf{p}}' = (\bar{x}' \bar{y}')\) を考える。以後、整数の座標値と実数の座標値を区別するために、整数の座標値には \(\bar{x}, \bar{y}\) のように上にバーを付けて表すことにする。

この変換後の位置に対応する変換前の画素の位置 \(\mathbf{p} = (x, y)\) は実数の座標値を持ち、座標変換 \(M\) を用いて

\[ \mathbf{p} = M^{-1} \bar{\mathbf{p}}' \]

のように書ける。ここで、 \(\mathbf{p}\) に対応する画素の値として、 \(\mathbf{p}\) に最も近い整数座標の画素、すなわち、

\[ \bar{\mathbf{p}} = (\lfloor x + 0.5 \rfloor, \lfloor y + 0.5 \rfloor) \]

に対応する画素値を用いるような補間法を 最近傍補間 と呼ぶ。

バイリニア補間

バイリニア補間は実数座標 \(\mathbf{p}\) の周囲の4つの画素の値を用いて、 \(\mathbf{p}\) に対応する画素の値を求める方法である。バイリニア補間に用いられる4つの近傍画素とは、それぞれ整数を座標値に持つ画素で、次の4つの位置を指す。

\[\begin{split} \begin{align*} \bar{\mathbf{p}}_{00} &= (\lfloor x \rfloor, \lfloor y \rfloor) \\ \bar{\mathbf{p}}_{01} &= (\lfloor x \rfloor, \lfloor y \rfloor + 1) \\ \bar{\mathbf{p}}_{10} &= (\lfloor x \rfloor + 1, \lfloor y \rfloor) \\ \bar{\mathbf{p}}_{11} &= (\lfloor x \rfloor + 1, \lfloor y \rfloor + 1) \end{align*} \end{split}\]

これら4つの位置に対応する画素値を線形補間に用いるパラメータ \(u, v\) を次のように定義する。

\[\begin{split} \begin{align*} u &= x - \lfloor x \rfloor \\ v &= y - \lfloor y \rfloor \end{align*} \end{split}\]

4つの位置に対応する画素値を \(I_{00}, I_{01}, I_{10}, I_{11}\) とすると、バイリニア補間によって求められる画素値 \(I(\mathbf{p})\) は次のように表される。

(4.4)\[ I(\mathbf{p}) = (1 - u)(1 - v) I_{00} + (1 - u)v I_{01} + u(1 - v) I_{10} + uv I_{11} \]

バイリニア補間に用いられる (4.4) は、以下のようなベクトルと行列の積によって書き換えられる。

\[\begin{split} I(\mathbf{p}) = \begin{pmatrix} 1 - u \\ u \end{pmatrix}^\top \begin{pmatrix} I_{00} & I_{01} \\ I_{10} & I_{11} \end{pmatrix} \begin{pmatrix} 1 - v \\ v \end{pmatrix} \end{split}\]

この補間方法はx方向の画素をパラメータ \(u\) で補間する操作とy方向の画素をパラメータ \(v\) で補間する双線型補間に対応するので、そこからバイリニア補間と呼ばれる。

バイキュービック補間

バイキュービック補間は、前述の2つの補間法と比べると少々複雑だが、実数座標 \(\mathbf{p} = (x, y)\) の周囲の4×4 = 16個の画素を用いて \(I(\mathbf{p})\) を求める方法である。この値は、 (4.4) のように、以下のようなベクトルと行列の積で書き表せる。

\[\begin{split} I(\mathbf{p}) = \begin{pmatrix} h(x_1) \\ h(x_2) \\ h(x_3) \\ h(x_4) \end{pmatrix}^\top \begin{pmatrix} I_{00} & I_{01} & I_{02} & I_{03} \\ I_{10} & I_{11} & I_{12} & I_{13} \\ I_{20} & I_{21} & I_{22} & I_{23} \\ I_{30} & I_{31} & I_{32} & I_{33} \end{pmatrix} \begin{pmatrix} h(y_1) \\ h(y_2) \\ h(y_3) \\ h(y_4) \end{pmatrix} \end{split}\]

本式に現れる \(h(x)\) は後述するsinc関数を三次式で近似したものであり、次の式で表せる。

\[\begin{split} h(x) = \begin{cases} (a + 2) x^3 - (a + 3) x^2 + 1 & (|x| < 1) \\ a x^3 - 5 a x^2 + 8 a x - 4 a & (1 \leq |x| < 2) \\ 0 & (2 \leq |x|) \end{cases} \end{split}\]

この式において \(a\) は補間関数の形を調整するパラメータで一般的には \(a = -0.5\) が用いられる。 \(a = -0.5\) の場合の \(h(x)\) は次のような形になる。

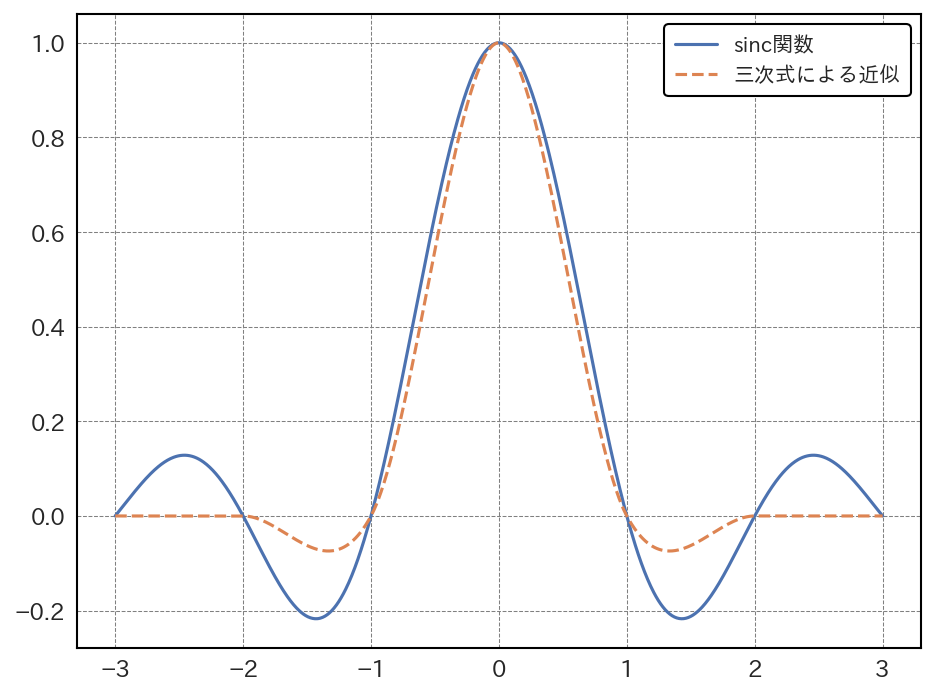
図 4.2 バイキュービック補間のためのsinc関数の近似式

sinc関数を用いると、一定の条件下で、元の連続信号を完全に復元できるという性質があり、バイキュービック補間はバイリニア補間よりも急峻な輝度の変化を復元できる。

一方で、バイキュービック補間の背景にある標本化定理は周波数空間の画像表現に大きく依存しており、エッジの周りが明るくなったり暗くなったりするような特有のアーティファクトが発生しやすいという欠点もある。

表 4.1 画像拡大における補間法の比較

最近傍補間	バイリニア補間	バイキュービック補間

インターエリア法

ここまでに紹介した3つの補間法は、「補間」、すなわち、サンプリングされている画素の値を用いて、その画素の間にあるであろう画素の値を推定する方法であった。このような「補間」は画像の拡大において必要となる操作であり、画像を縮小する場合には別の処理を考える必要がある。

画像を縮小すると、縮小後の画像の1画素には、縮小前の画像の複数の画素が対応することになるので、その中から1画素だけを選んで、縮小後の画素値とすると、不自然な結果となる。また、バイキュービック補間で用いる画素が4×4の領域であるので、縮小率が一定以上になると、バイキュービック補間でも、縮小後の画素に対応する複数の画素の影響を十分に反映することができなくなる。

このような理由から、画像の縮小を行う場合には、インターエリア法 (inter-area method) と呼ばれる方法を用いることがある。インターエリア法は、縮小前の画像の画素の値をそのまま用いるのではなく、縮小前の画像の画素の値を平均化して、縮小後の画素に対応する画素値とする方法である。

この方法は、縮小後の画像の画素に対応する縮小前の画素の平均値を求める必要があるので、計算量が増えるという欠点がある。しかし、インターエリア法は、縮小後の画像の画素に対応する複数の画素の影響を十分に反映できるので、画像を縮小する場合においては、バイキュービック補間等よりも自然な結果になることが多い。

バイキュービック補間	インターエリア法

上の画像に示す通り、画像の縮小にバイキュービック補間を用いると、ジャギーがかったような結果になる。これは、縮小前の画像上で対応する位置の周辺画素しか用いていないためで、そのため、サンプルされる画素が飛び飛びになってジャギーのようなアーティファクトが発生する。一方、インターエリア法の場合には、縮小後の画素に対応する領域に含まれる 縮小前の画像の画素全て を平均するので、ややボケた見た目にはなるものの、画像として自然な縮小結果となっていることが確認できる。

4.3. 標本化定理

Shannon-Nyquistの 標本化定理 は、画像における標本化を考える上で非常に重要な定理である。この定理が直接的に述べていることは以下のようなことである。

とある信号が周波数 \(f_{\text{max}}\) 以下の成分のみを持つ場合、サンプリング周波数を \(2f_{\text{max}}\) 以上、すなわちサンプリング間隔を \(T = 1 / (2 f_{\text{max}})\) 以下にして標本化を行うと、元の信号を完全に復元することができる。

これはにわかには理解しがたいが、直感的には、より細かな特徴 (= \(f_{\text{max}}\) が大きな成分を持つ) を持つ信号を標本化する場合、元の信号を正しく復元するには、より細かな間隔でサンプリングをする必要がある、ということを述べている。元の信号を復元するのに必要な最低のサンプリング周波数 \(2f_{\text{max}}\) を Nyquist周波数 と呼ぶ。

では、実際に、一定の周波数以下の成分だけを持つ一次元信号を標本化して、標本化定理の主張が正しいかを検証してみよう。今回は、2つの正弦関数を組み合わせた次の関数 \(h(x)\) を考える。

\[ h(x) = \sin(x) + \frac{1}{2} \sin\left(2 x + \frac{\pi}{2}\right) \]

\(h(x)\) は周期がそれぞれ \(2 \pi\) と \(\pi\) の正弦波の和であるので、最大の周波数は \(f_{\text{max}} = \frac{1}{\pi}\) である。\(h(x)\) をプロットすると、次のようになる。

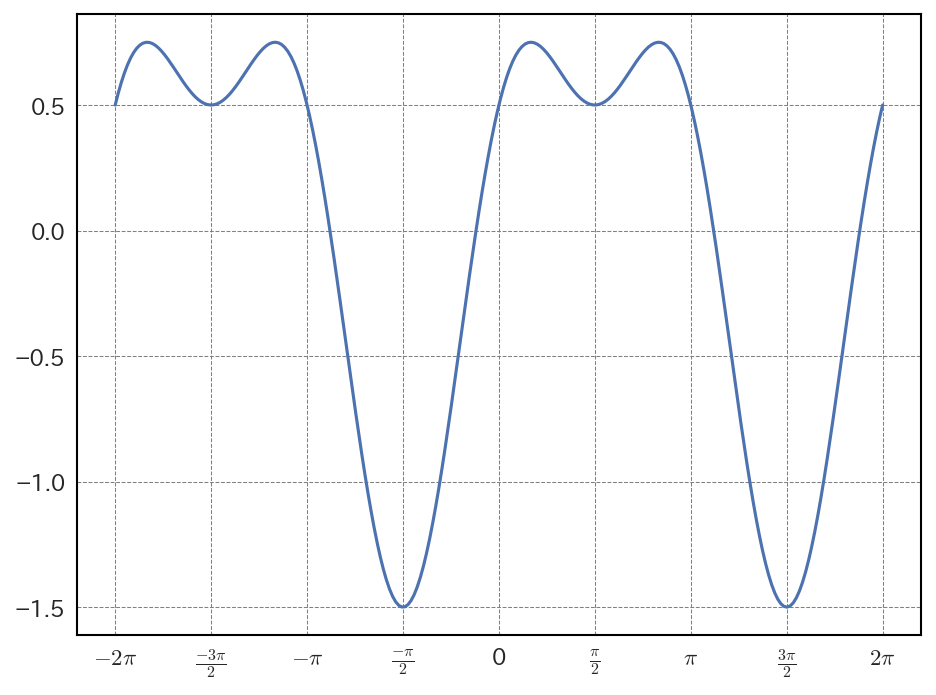
標本化定理によれば、サンプリング間隔を \(T = \frac{1}{2 f_{\text{max}}} = \frac{\pi}{2}\) 以下に設定すれば元の関数が再現できる。この間隔で取られたサンプル点 \((x_n, y_n)\) とすると、

\[\begin{split} \begin{align*} x_i &= n T \\ y_i &= h(x_n) = h(n T) \end{align*} \end{split}\]

のように表せる。これらのサンプル点を使って \(h(x)\) を復元するには、sinc関数 (ジンクかんすう、シンクかんすう)と呼ばれる次の関数を用いる。

\[ \text{sinc}(x) = \frac{\sin(x)}{x} \]

具体的には、次の無限級数によって元の関数 \(h(x)\) を完全に復元することができる。

(4.5)\[ h(x) = \sum_{n=-\infty}^{\infty} y_n \text{sinc}\left(\frac{\pi (x - x_n)}{T}\right) \]

\(T = \frac{\pi}{2}\) を使用し、(4.5) を用いて復元された \(h(x)\) と、元の \(h(x)\) を比較してみよう。以下に、コード例と復元結果の比較を示す (NumPyの np.sinc は \(\mathrm{sinc}(\pi x)\) に対応することに注意)。

import numpy as np
import matplotlib.pyplot as plt

# サンプリング間隔
T = np.pi * 0.5

# 実際の関数
xs = np.linspace(-2.0 * np.pi, 2.0 * np.pi, 250, endpoint=True)
ys = func(xs)

# 復元に用いる点. 十分に広い範囲からサンプルしておく
xn = np.arange(-100, 101) * T
yn = func(xn)

# 関数の復元
rec = np.zeros_like(xs)
for i in range(len(xs)):
    for j in range(len(xn)):
        rec[i] += yn[j] * np.sinc((xs[i] - xn[j]) / T)

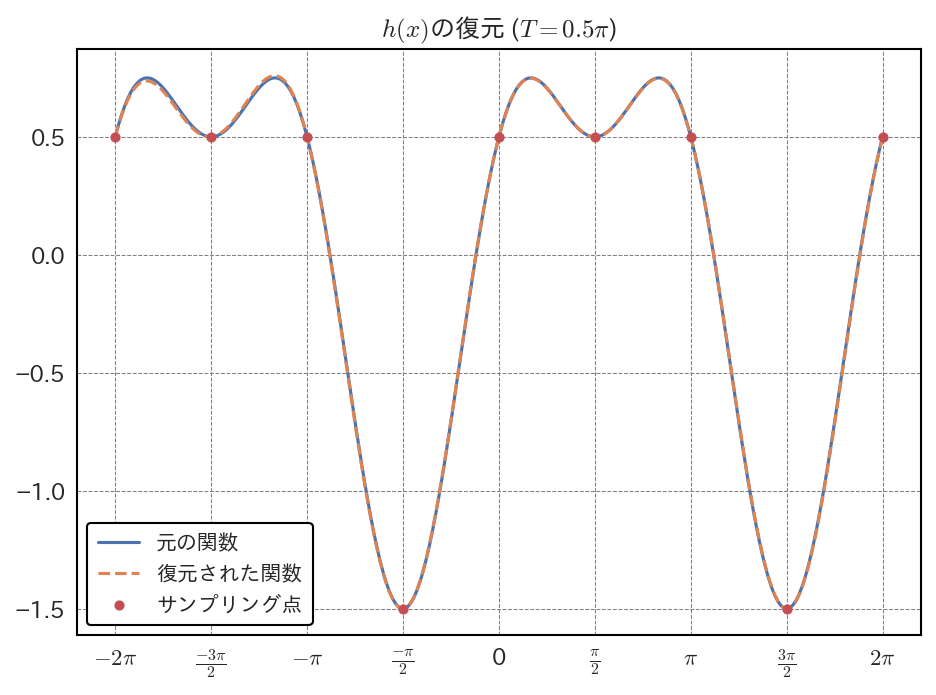
しかし、このサンプリング間隔をわずかに大きくして \(T = 0.51 \pi\) とすると、次のような関数が得られる。

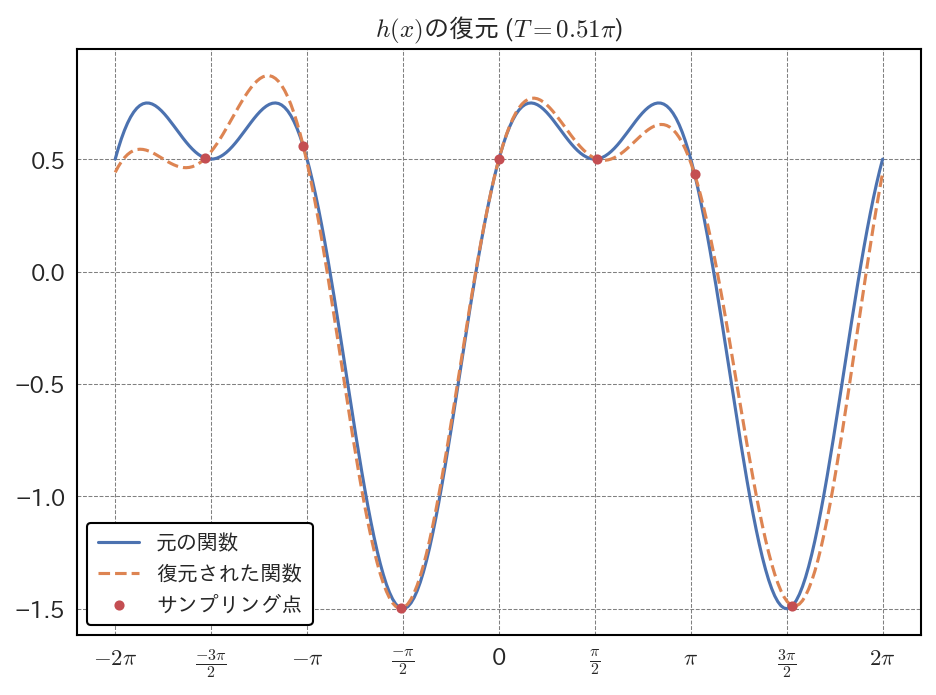
図 4.3 サンプル間隔をわずかに大きくした場合の復元結果

図 4.3 の復元結果には元の信号に含まれている周波数とは異なる周波数の成分が現れてしまっている。このように標本化の影響で、元の信号に含まれていない周波数成分が現れる現象を エイリアシング (aliasing) と呼ぶ。

また画像処理の分野では、エイリアシングの影響で現れる本来は存在しないはずの周波数を持った縞模様のようなアーティファクトを モアレ (moiré) と呼ぶ。

練習問題

上記のソースコードを編集し、サンプリング間隔を \(T = \frac{\pi}{2}\) より大きく、または小さくした場合に、復元される関数がどのようになるかを確認せよ。

4.3.1. 標本化定理の証明

標本化定理を証明するにあたりサンプリングを数式として表すことを考えてみる。サンプリング間隔を \(T\) とすると、理想的なサンプリングはDiracのデルタ関数 \(\delta(x)\) を用いて次のように表せる。

(4.6)\[ g(x) = h(x) \sum_{n=-\infty}^{\infty} \delta(x - n T) = \sum_{n=-\infty}^{\infty} h(n T) \delta(x - n T) \]

この式において

\[ \text{comb}_{T}(x) \sum_{n=-\infty}^{\infty} \delta(x - n T) \]

の部分はDiracの櫛形関数 (Dirac's comb function)と呼ばれる。櫛形関数は、サンプリング間隔を \(T\) ごとにDiracのデルタ関数が並んだような関数である。

定義から櫛形関数は周期 \(T\) を持つ周期関数であるので、Fourier級数展開を用いて表せる。

\[ \text{comb}_{T}(x) = a_0 + \sum_{n=1}^{\infty} \left( a_n \cos\left(\frac{2 \pi n x}{T}\right) + b_n \sin\left(\frac{2 \pi n x}{T}\right) \right) \]

この時、Fourier級数の各係数を求めるのに必要な積分区間が \([-\frac{T}{2}, \frac{T}{2}]\) であって、この区間内には一つのDiracのデルタ関数だけが含まれることに着目すると、各級数は次のように求められる。

\[\begin{split} \begin{align*} a_0 &= \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} \delta(x) dx = \frac{1}{T} \\ a_n &= \frac{2}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} \delta(x) \cos\left(\frac{2 \pi n x}{T}\right) dx = \frac{2}{T} \cos\left( \frac{2 \pi n 0}{T} \right) = \frac{2}{T} \\ b_n &= \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} \delta(x) \sin\left(\frac{2 \pi n x}{T}\right) dx = \sin\left( \frac{2 \pi n 0}{T} \right) = 0 \end{align*} \end{split}\]

となる。従って、Diracのデルタ関数のFourier級数展開は次のように表せる。

\[ \text{comb}_{T}(x) = \frac{1}{T} + \sum_{n=1}^{\infty} \frac{2}{T} \cos\left(\frac{2 \pi n x}{T}\right) \]

従って、\(h(x)\) を標本化して得られる関数 \(g(x)\) は次のように書ける。

\[\begin{split} \begin{align*} g(x) &= h(x) \text{comb}_{T} (x) \\ &= \frac{1}{T} h(x) + \frac{2}{T} h(x) \cos\left( \frac{2 \pi x}{T} \right) + \frac{2}{T} h(x) \cos\left( \frac{4 \pi x}{T} \right) + \cdots \end{align*} \end{split}\]

この級数の両辺をFourier変換することを考える。なお、 \(g(x)\) ならびに \(h(x)\) のFourier変換は \(G(x)\) と \(H(x)\) で表すことにする。各項のFourier変換を計算してみよう。

\[ \cos\left( \frac{2 \pi n x}{T} \right) = \frac{e^{i \frac{2 \pi n x}{T}} + e^{-i \frac{2 \pi n x}{T}}}{2} \]

であることを利用すると、第2項のFourier変換は次のように計算できる。

\[\begin{split} \begin{align*} & \int_{-\infty}^{\infty} h(x) \cos\left(\frac{2 \pi n x}{T} \right) e^{-i \omega x} \mathrm{d} x \\ =& \frac{1}{2} \int_{-\infty}^{\infty} h(x) e^{-i \left( \omega - \frac{2 \pi n}{T} \right) x} \mathrm{d} x + \frac{1}{2} \int_{-\infty}^{\infty} h(x) e^{-i \left( \omega + \frac{2 \pi n}{T} \right) x} \mathrm{d} x \\ =& \frac{1}{2} H\left( \omega - \frac{2 \pi n}{T} \right) + \frac{1}{2} H\left( \omega + \frac{2 \pi n}{T} \right) \end{align*} \end{split}\]

したがって、 \(g(x)\) のFourier変換は次のように表せる。

\[ G(\omega) = \frac{1}{T} H(\omega) + \sum_{n=1}^{\infty} \frac{1}{T} \left( H\left( \omega - \frac{2 \pi n}{T} \right) + H\left( \omega + \frac{2 \pi n}{T} \right) \right) \]

ここで \(h(x)\) が帯域制限された関数であったことを思い出してほしい。従って、 \(H(\omega)\) はとある実数 \(B\) に対して \([-B, B]\) の範囲外では0である。

ここで、\(G(\omega)\) をプロットすると、下図のようになると考えられる。

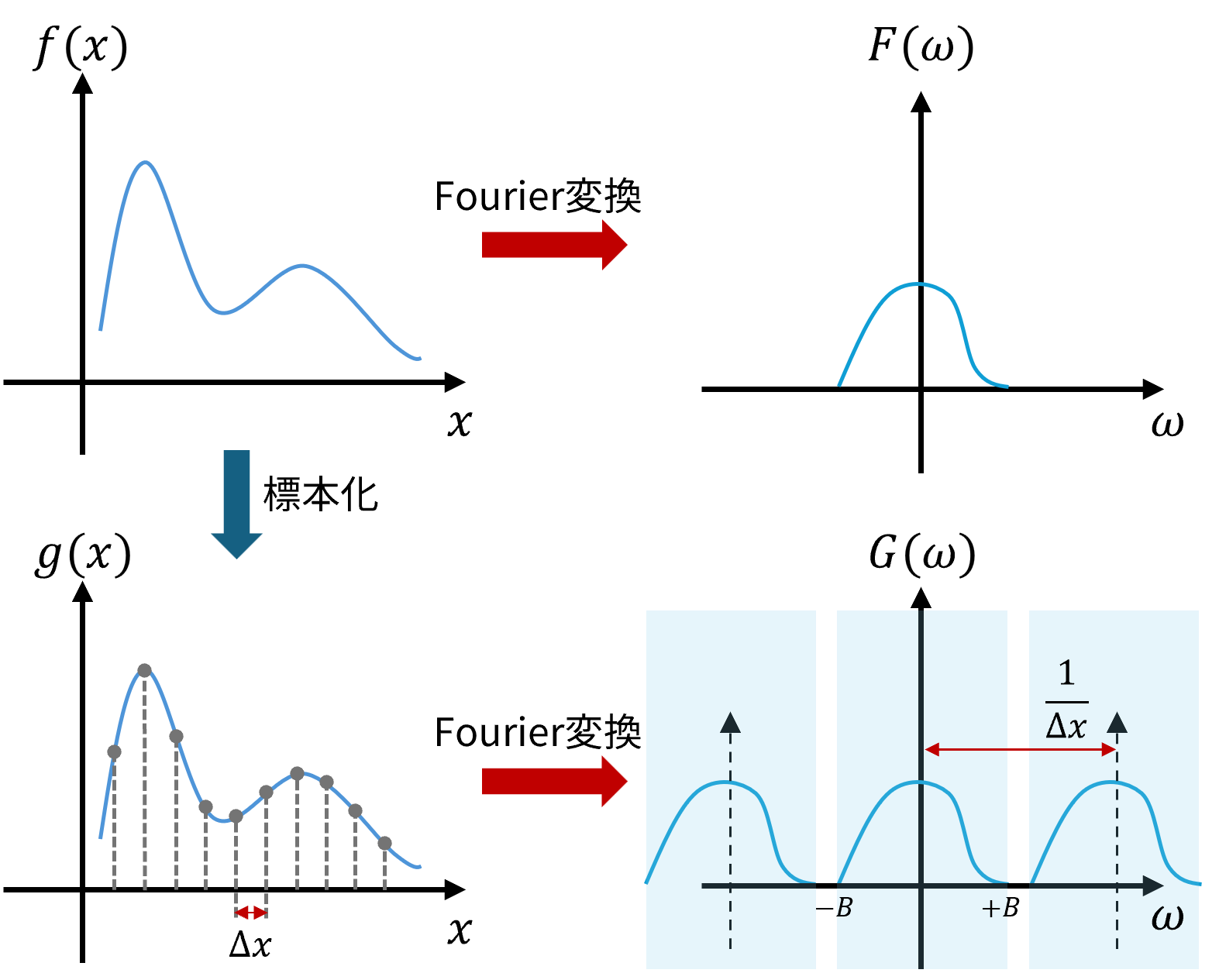
図 4.4 標本化前後の信号とそのFourier変換の関係

このプロット上では \(H(\omega)\) が一定間隔 \(\frac{2 \pi}{T}\) ごとに繰り返されていることが分かる。この各 \(H(\omega)\) のコピーのことを特に レプリカ (replica) と呼ぶ。各レプリカが十分に離れていれば、中央のレプリカ \(H(\omega)\) に \([-\frac{\pi}{T}, \frac{\pi}{T}]\) の範囲内でだけ1を取るような矩形関数をかけて逆Fourier変換を行えば、元の関数 \(h(x)\) を完璧に復元できる。

今、基本の矩形関数を次のように定義する。

\[\begin{split} \text{rect}(x) = \begin{cases} 1 & |x| < \frac{1}{2} \\ 0 & \text{otherwise} \end{cases} \end{split}\]

このような矩形関数のFourier変換は次のように書ける。

\[ \mathcal{F} \left\{ \text{rect}(x) \right\} = \text{sinc}(\frac{\omega}{2}) \]

矩形関数が幅\(2B\)を保つ場合には、定義域全体での積分結果が1になるように正規化した次の式を用いる

\[\begin{split} \text{rect}_{2B}(x) = \frac{1}{2B} \text{rect}\left( \frac{x}{2B} \right) = \begin{cases} \frac{1}{2B} & |x| \leq B \\ 0 & \text{otherwise} \end{cases} \end{split}\]

この矩形関数のFourier変換はsinc関数を用いて次のように書ける。

\[ \mathcal{F} \left\{ \text{rect}_{2B}(x) \right\} = \text{sinc}\left( B \omega \right) \]

今求めたい関数は周波数空間における \(G(\omega)\) と \(\text{rect}_{\frac{2\pi}{T}}(\omega)\) の積を逆Fourier変換したものである。Fourier変換の性質から、関数の積のFourier変換は変換後の関数の畳み込みで表せる。すなわち、

\[ \mathcal{F} \left\{ f \ast g \right\} = F \cdot G \]

である。従って、復元される信号 \(\hat{h}(x)\) は次のように表せる。

\[\begin{split} \begin{align*} \hat{h}(x) &= \mathcal{F}^{-1} \left\{ G(\omega) \cdot \text{rect}_{2B}(\omega) \right\} \\ &= \mathcal{F}^{-1} \left\{ G(\omega) \right\} \ast \mathcal{F}^{-1} \left\{ \text{rect}_{\frac{2\pi}{T}}(\omega) \right\} \\ &= g(x) \ast \text{sinc}\left( \frac{\pi x}{T} \right) \end{align*} \end{split}\]

ここで(4.6)に示した \(g(x)\) の定義を思い出してほしい。 \(g(x)\) は \(h(x)\) と櫛形関数の積であり、定義に現れる無限級数の各項は \(h(x) \delta(x - n T)\) であった。この項とsinc関数の畳み込みを考えると、次のような式が得られる。

\[\begin{split} \begin{align*} & \left[ h(x) \delta(x - n T) \right] \ast \text{sinc}\left( \frac{\pi x}{T} \right) \\ = & \int_{-\infty}^{\infty} h(t) \delta(t - n T) \text{sinc}\left( \frac{\pi (x - t)}{T} \right) \mathrm{d} t \\ = & h(n T) \text{sinc}\left( \frac{\pi (x - nT)}{T} \right) \\ \end{align*} \end{split}\]

従って、 \(\hat{h}(x)\) は次のように表せる。

\[ \hat{h}(x) = \sum_{n=-\infty}^{\infty} h(n T) \text{sinc}\left( \frac{\pi (x - nT)}{T} \right) = \sum_{n=-\infty}^{\infty} y_n \text{sinc}\left( \frac{\pi (x - x_n)}{T} \right) \]

以上より、 (4.5) に示した完全復元の式が得られた。

4.3.2. エイリアシングの正体

エイリアシングは、信号の持つ空間周波数よりも一定以上低いサンプリング周波数を用いたときに発生するアーティファクトである。

実はこのエイリアシングの正体は 図 4.4 から説明できる。 図 4.4 では元の信号の周波数 \(f(x)\) が最大 \(B\) で帯域制限されており、 \(f(x)\) のFourier変換である \(F(\omega)\) は \(\omega \in [-B, +B]\) の外側では常に0を取る。そのため、 \(f(x)\) をサンプリング間隔 \(\Delta x\) で標本化する場合、サンプリング間隔 \(\Delta x\) が \(\frac{1}{\Delta x} > 2B\) を満たす, すなわち \(\Delta x < \frac{1}{2B}\) より細かい間隔でサンプリングされていれば、標本化後の信号 \(g(x)\) のFourier変換 \(G(\omega)\) に現れるレプリカは同士が重ならずに済む。

一方で、サンプリング間隔が十分に小さくない場合には、標本化後の信号 \(g(x)\) のFourier変換 \(G(\omega)\) の中でレプリカ同士が重なり合ってしまい、適当な領域を切り取るなどの操作で、元の信号 \(f(x)\) を復元できなくなる。このような場合に現れるアーティファクトが エイリアシング である。

このような、元の信号に含まれない周波数成分の混入は、前述の

\[ h(x) = \sin(x) + \frac{1}{2} \sin\left(2 x + \frac{\pi}{2}\right) \]

のような単純な波の重ね合わせを考えれば容易に理解できる。 \(h(x)\) のFourier変換は次のように表せる。

\[ H(\omega) = i \pi \left( \delta(\omega + 1) - \delta(\omega - 1) \right) + \frac{i \pi}{2} \left( \left( \delta(\omega + 2) - \delta(\omega - 2) \right) \right) \]

この \(H(\omega)\) は \(\omega = \pm 1, \pm 2\) にしか非零の値を持たず、 \(| \omega | \geq 2\)　で帯域制限されているわけだが、レプリカ同士が重なり合うと、帯域内の異なる \(\omega\) でも比例の値を取るようになり、結果としてその周波数成分がエイリアシングとして現れる。