9. 深層学習

深層学習 とは多層のニューラルネットを用いる機械学習モデルのことである。

人工的なニューラルネット (artificial neural network)は、人間の脳におけるニューロンのシナプスを介した情報伝達網 (biological neural network)を模したモデルとして1950年代から研究されていた。

多層のニューラルネットの考え方を最初に提唱したのは、当時NHKの放送技術研究所の研究員であった福島邦彦 が提案した ネオコグニトロン (neocognitron) であると言われている。驚くべきことに、その論文は1980年に出版されている [32]。

これは2024年にノーベル物理学賞を獲得したJeffery Hintonの代表研究である誤差逆伝搬の論文[33] (1986年発表) や、John HopfieldのHopfieldネットワークの論文[34] (1982年発表)よりも前である。

ただし、ネオコグニトロンが提案された1980年代は、ニューラルネットワークの持つ多数のパラメータを上手く最適化する手法がなく、その時代には今で言う深層ニューラルネットの実現は難しいと考えられていた。事実、当時のニューラルネットは入力層、隠れ層、出力層の三層から成るニューラルネットが主流であった。

しかし、2010年代に入ると、それまで下火だったニューラルネットが再び注目を集めることになる。

それまで細々と続けられていたニューラルネットワークの研究の中で、パラメータの過学習や、最適化時の勾配消失といった問題が徐々に解決されるとともに、GPUを用いた汎用計算であるGPGPU (General Purpose Computing on GPU)により並列計算の効率が大幅に上昇するなど、ニューラルネットワークを取り巻く環境が徐々に変化してくる。

ImageNetと呼ばれる大規模画像データセットの識別チャレンジであるILSVRC (ImageNet Large Scale Visual Recognition Challenge)において、トロント大学のGeoffrey Hintonらの研究チームが、AlexNet (筆頭著者のfirst nameから)と呼ばれるニューラルネットを用いて優勝する [35]。

AlexNetはエラー率わずか17.0％を達成したが、その性能は2位チームのエラー率26.2%を大幅に上回るものであった。ちなみに、この時に2位に入賞したチーム(東京大学の研究グループ)が用いた手法はSIFT, Fisherベクトル, サポートベクトルマシンを組み合わせたものであった。

この優勝を皮切りに、2013年の大会ではオックスフォード大学のチームがVGGというネットワークで2位に入り、以後、2014年はGoogleのチームが GoogLeNet というネットワークで2位、2015年はMicrosoftのチームが ResNet というネットワークで優勝した。

すると、画像認識の分野では深層学習がさかんに研究されるようになり、その応用が生成モデルや強化学習など、様々な分野に広がって現在に至る。本節では、画像の認識と生成における深層学習の基礎について順を追って見ていこう。

参考資料

• 『ディジタル画像処理 改訂第二版』 P.293 第13章 深層学習による画像認識と生成

• 『深層学習』 編: 神嶌 敏弘, 著: 麻生 英樹ら

9.1. ニューラルネット

本節の冒頭で述べた通り、ニューラルネットは生物の脳神経系に着想を得た計算モデルである。

生物の脳内では複数のニューロンがシナプスで結合されており、ニューロンはシナプスを介して他のニューロンと情報をやり取りしている。ニューロンは、他のニューロンからの入力信号がある閾値を超えると、活動電位と呼ばれる信号を発生させる。この活動電位は、他のニューロンに伝達され、次のニューロンの活動を引き起こす。

この活動を計算機で模倣したものが ニューラルネットワーク (artificial neural network)である。通常、生物のニューロンは多くの別のニューロンと結合していて、その結合網は複雑なグラフ構造となっているが、これを計算機上で模倣しようとすると処理が複雑になりすぎてしまう恐れがある。

そのため、現代につながるニューラルネットでは、ニューロンを層状に配置し、隣接する層と層の間での情報伝達を考える 階層的ニューラルネット を用いるのが一般的である。

9.1.1. 階層型ニューラルネット

ここでは単純な階層型のニューラルネットとして、入力層、隠れ層、出力層の3つの層を持つモデルを考えよう。

各層のニューロンは自分が発火しているのかしていないのかを表す0か1かの数値を持っている。これを数学的に表すなら、入力層、隠れ層、出力層のそれぞれがもつ情報をベクトル \(\mathbf{x} \in \{ 0, 1 \}^{N_1}\), \(\mathbf{h} \in \{ 0, 1 \}^{N_2}\), \(\mathbf{y} \in \{ 0, 1 \}^{N_3}\) で表すことになる (\(N_1\), \(N_2\), \(N_3\)はそれぞれの層のニューロン数)。

今、とある層のニューロンが次の層のニューロン全てに接続されているとすれば、そのニューロン間の接続の強さを行列で表すことができる。すなわち、入力層から隠れ層への接続の強さは \(\mathbf{W}_{1} \in \mathbb{R}^{N_2 \times N_1}\)、隠れ層から出力層への接続の強さは \(\mathbf{W}_{2} \in \mathbb{R}^{N_3 \times N_2}\) のように表すことができる。

情報を受け取った各ニューロンは、受け取った値が、あるしきい値 (例えば0.5)を超えていたら1、そうでなければ0を取るような活性化される。従って、しきい値処理を行う関数を

\[\begin{split} \sigma(x) = \begin{cases} 0 & (x < 0.5) \\ 1 & (x \geq 0.5) \end{cases} \end{split}\]

のように書くことにすると、隠れ層の各ニューロンの発火状態は、入力層のニューロンの発火状態を用いて次の式で書き表せる。

\[ \mathbf{h} = \sigma(\mathbf{W}_{1} \mathbf{x}) \]

同様に、出力層のニューロンの発火状態は、隠れ層のニューロンの発火状態を用いて次の式で書き表せる。

\[ \mathbf{y} = \sigma(\mathbf{W}_{2} \mathbf{h}) \]

このように入力から出力に向かって情報を順々に伝達する操作を フィードフォワード (feedforward)と呼ぶ。

機械学習モデルとしてのニューラルネットは、訓練データセット上で定義された入力 \(\mathbf{x}\) に対して、それにふさわしい出力 \(\mathbf{y}\) を返すように訓練される。従って、この3層のニューラルネットでは \(\mathbf{W}_{1}\), \(\mathbf{W}_{2}\)の2つの行列を訓練データに合うように最適化すれば良い。

9.1.2. 誤差逆伝播法

誤差逆伝搬法 (backpropagation) [33] は、階層型ニューラルネットを効率的に訓練するためのテクニックの一つである。

この方法では、不連続なしきい値処理を行っていた活性化関数 \(\sigma\) を連続的な関数に置き換える。しきい値処理を滑らかな関数で置き換えたシグモイド関数

\[ \sigma(x) = \frac{1}{1 + e^{-x}} \]

を用いると、活性化関数が微分可能になる。

すると、出力層の発火状態 \(\mathbf{y}\) を、入力層の発火状態に関する連続的な関数として表すことができるようになる。具体的には、シグモイド関数 \(\sigma\) を用いて、次の関係式が得られる。

\[ \mathbf{y} = \sigma(\mathbf{W}_{2} \sigma(\mathbf{W}_{1} \mathbf{x})) \]

すると、出力 \(\mathbf{y}\) を入力や隠れ層の状態、あるいは重み行列 \(\mathbf{W}_{1}\), \(\mathbf{W}_{2}\) に関して微分できるようになる。例えば、出力 \(\mathbf{y}\) を重み行列 \(\mathbf{W}_{2}\) に関して微分すると、次のような式が得られる。

(9.1)\[\begin{split} \begin{align*} \frac{\partial \mathbf{y}}{\partial \mathbf{W}_{2}} &= \frac{\partial \sigma(\mathbf{W}_{2} \sigma(\mathbf{W}_{1} \mathbf{x}))}{\partial \mathbf{W}_{2}} \\ &= \sigma'(\mathbf{W}_{2} \sigma(\mathbf{W}_{1} \mathbf{x})) \sigma(\mathbf{W}_{1} \mathbf{x})^\top \\ &= \sigma'(\mathbf{W}_{2} \mathbf{h}) \mathbf{h}^\top \end{align*} \end{split}\]

同様にして、出力 \(\mathbf{y}\) を重み行列 \(\mathbf{W}_{1}\) に関して微分すると、次のような式が得られる。

(9.2)\[\begin{split} \begin{align*} \frac{\partial \mathbf{y}}{\partial \mathbf{W}_{1}} &= \frac{\partial \sigma(\mathbf{W}_{2} \sigma(\mathbf{W}_{1} \mathbf{x}))}{\partial \mathbf{W}_{1}} \\ &= \sigma'(\mathbf{W}_{2} \sigma(\mathbf{W}_{1} \mathbf{x})) \frac{\partial \sigma(\mathbf{W}_{1} \mathbf{x})}{\partial \mathbf{W}_{1}} \\ &= \sigma'(\mathbf{W}_{2} \mathbf{h}) \sigma'(\mathbf{W}_{1} \mathbf{x}) \mathbf{x}^\top \\ &= \sigma'(\mathbf{W}_{2} \mathbf{h}) \sigma'(\mathbf{W}_{1} \mathbf{x}) \mathbf{x}^\top \end{align*} \end{split}\]

ここで大事なことは、(9.1)と(9.2)は一部の項 (\(\sigma'(\mathbf{W}_{2} \mathbf{h})\))が共通しているという点である。

実は、階層型ニューラルネットの入力に近い方の層の変数による微分は、出力に近い方の変数による微分の値を用いて、出力に近い方から順に計算できる。これは、ニューラルネットが複数の関数の合成となっているためで、合成関数の微分の 連鎖律 (chain rule)が利用できるためである。

この連鎖律を利用して、出力に近い方の層から順に微分を計算していく手法を 誤差逆伝播法 と呼ぶ。

まとめ: ニューラルネット

• ニューラルネットは元々、生物の脳神経系に着想を得た計算モデルであった

• 現在は複数の層を持つ階層型ニューラルネットが主流である

• ニューラルネットのパラメータの最適化は誤差逆伝搬法を用いて効率化できる

9.2. 深層学習への歩み

ニューラルネットに関する研究において、今日の深層学習に大きな影響を与えたものはいくつもあるが、その中でも特に重要なものとして、2024年にノーベル物理学賞を受賞したJohn Hopfieldの Hopfieldネットワーク [34]、Geoffrey Hintonの 制限Boltzmannマシン (Restricted Boltzmann Machine, RBM) [36] について紹介しよう。

これら2つの技術は、ニューラルネットに与えられた複数の情報を記憶させる 連想記憶 のための手法である。考えてみると、ものごとの認識や生成というのは、人間の場合も何らかの過去の記憶を頼りにしていることが多い。その意味で、これらの2つの研究が提案した連想記憶の技術は、今日の深層学習モデルが行う認識や生成の基礎であるとも言える。

9.2.1. Hopfieldネットワーク

Hopfieldネットワークは、1982年にJohn Hopfield氏が提唱した、連想記憶 (associative memory)のためのニューラルネットである。

Hopfieldネットワークは、複数のニューロンを持ち、全てのニューロンがその他の全てのニューロンと結合している。各ニューロンは自分以外のニューロンに情報を伝達して、次の状態へと遷移する。

この時、Hopfieldネットワークの各ニューロンは、生物のニューロンにおける学習則の一つである Hebb則 (Hebbian rule)に着想を得た情報の伝達を行う。

Hebb則とは、シナプスにおいて情報を発出する側の前細胞と、情報を受け取る側の後細胞の間での結合の強化に関する学習則である。具体的には次のようなものである。

とある前細胞Aが後細胞Bに情報を伝達し、結果として後細胞Bが発火した場合、前細胞Aと後細胞Bの間の結合が強化される。

Hebb則を数学的に表現すると、\(n\)個の前細胞の発火状態 \(\mathbf{x} \in \{ 0, 1 \}^n\) と、\(m\)個の後細胞の発火状態 \(\mathbf{y} \in \{ 0, 1 \}^m\) の間で、情報の伝達を表す行列 \(\mathbf{W} \in \mathbb{R}^{m \times n}\) が次のように変化する。

(9.3)\[ \frac{\partial \mathbf{W}}{\partial t} = \mathbf{y} \mathbf{x}^\top \]

一方で、Hopfieldネットワークには前細胞や後細胞などの区別はなく、(9.3)を簡易化した次のような式を用いる。

\[ \frac{\partial \mathbf{W}}{\partial t} = \mathbf{x} \mathbf{x}^\top \]

ただし、Hopfieldネットワークで扱う発火状態は-1か+1のいずれかの値をとる (つまり \(\mathbf{x} \in \{ -1, +1 \}^n\)) 。また、各ニューロンは自分自身には情報伝達をしないので、 \(\mathbf{W}\) の対角成分は常に0であるとする。

Hopfieldネットワークは複数の-1と+1からなるパターンを記憶することができ、そのパターンに似たノイズを含む入力を与えると、ニューロンの発火状態が記憶したパターンに収束するという性質を持つ。

実際に、Hopfieldネットワークに0, 1, 2の数字を模した5×5のパターンを記憶させ、その後、ノイズ付きの入力を与えて得られた画像を以下に示す。

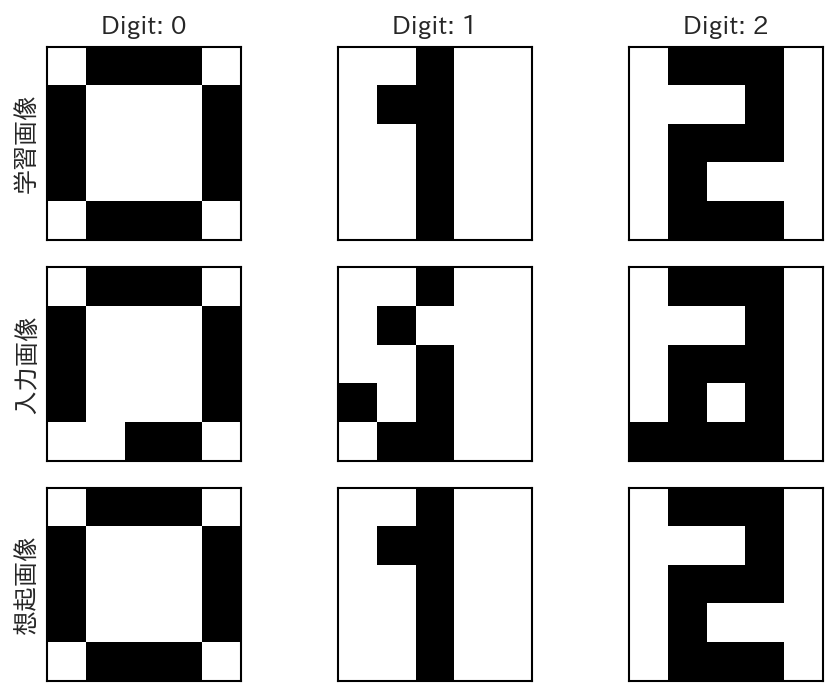
図 9.1 Hopfieldネットワークによる数字の想起結果

このように記憶するデータの数が比較的少数で、なおかつノイズの量が少ない場合については、Hopfieldネットワークが正しくパターンを記憶できていることが分かる。

9.2.2. 制限Boltzmannマシン (RBM)

制限Boltzmannマシン (Restricted Boltzmann Machine, RBM) は、1986年にGeoffrey Hinton氏が提唱した、確率的な連想記憶モデルであり、Hopfieldネットワークを確率的な表現を用いて拡張したものと位置づけられる。

RBMの前身であるBoltzmannマシンは、Hopfieldネットワークと同様に、全てのニューロンが他の全てのニューロンと結合しているニューラルネットであった。一方で、「制限」Boltzmannマシンのニューラルネットは、可視層 (visible layer)と隠れ層 (hidden layer)の2つの層を持ち、可視層と隠れ層のニューロンは互いに結合したような階層的ニューラルネットになっている。

今、RBMの可視層が持つニューロンの状態を \(\mathbf{x} \in \{ 0, 1 \}^{N_1}\)、隠れ層が持つニューロンの状態を \(\mathbf{h} \in \{ 0, 1 \}^{N_2}\) と表す。この際、ニューロンの状態を-1か+1かで表していたHopfieldネットワークと異なり、ニューロンの状態が0か1かで表されていることに注意してほしい。

RBMは可視層で情報を受け取ると、それを重み行列 \(\mathbf{W} \in \mathbb{R}^{N_2 \times N_1}\) とバイアスベクトル \(\mathbf{c} \in \mathbb{R}^{N_2}\) に基づいて用いて隠れ層に伝達する。

(9.4)\[ \mathbf{h} = \sigma(\mathbf{W} \mathbf{x} + \mathbf{c}) \]

RBMは、Hopfieldネットワークと異なり、隠れ層に伝達された情報が、シグモイド関数 \(\sigma\) を使って確率的に発火するようなモデルになっている。そのため、隠れ層に伝達された情報は0から1の間の実数値で、各ニューロンの発火確率を表す。

隠れ層のニューロンは、さらにその情報を可視層に伝達する。重み行列 \(\mathbf{W}\) が再利用され、バイアスベクトルとしては別の \(\mathbf{b} \in \mathbb{R}^{N_1}\) を用いる。

(9.5)\[ \mathbf{y} = \sigma(\mathbf{W}^\top \mathbf{h} + \mathbf{b}) \]

可視層ではシグモイド関数を用いて各ニューロンの発火確率が計算される。最終的に、この発火確率が0.5より大きければ、そのニューロンが発火しているとみなして出力を得る。

RBMは連想記憶のモデルであるので、入力された画像がパラメータ \(\Theta = \{ \mathbf{W}\), \(\mathbf{b}\), \(\mathbf{c} \}\) によって再現されることを期待している。

この際、ある入力画像 \(\mathbf{v}\) に対して、RBMは次の同次分布を考える。

(9.6)\[\begin{split} \begin{gather*} p(\mathbf{v}, \mathbf{h}) = \frac{1}{Z(\Theta)} \exp\left(-E(\mathbf{v}, \mathbf{h} \mid \Theta)\right) \\ E(\mathbf{v}, \mathbf{h} \mid \Theta) = -\mathbf{v}^\top \mathbf{W} \mathbf{h} - \mathbf{b}^\top \mathbf{v} - \mathbf{c}^\top \mathbf{h} \end{gather*} \end{split}\]

ただし、\(Z(\Theta)\) は \(p(\mathbf{v}, \mathbf{h} \mid \Theta)\) を正規化するための規格化定数で

(9.7)\[ Z(\Theta) = \sum_{\mathbf{v}, \mathbf{h}} \exp\left(- E(\mathbf{v}, \mathbf{h} \mid \Theta)\right) \]

とする。

この確率密度関数の定義には \(\mathbf{v}\) 同士または \(\mathbf{h}\) 同士の積は存在せず、これはRBMの構造において、可視層と隠れ層の間でだけ結合が存在することを示している。

このことから、一度、可視層が固定されれば、隠れ層のニューロン同士は独立に発火状態が決まるため、事後分布 \(p(\mathbf{h} \mid \mathbf{v}, \Theta)\) は次のように書ける。

\[ p(\mathbf{h} \mid \mathbf{v}, \Theta) = \prod_{i=1}^{N_2} p(h_i \mid \mathbf{v}, \Theta) = \prod_{i=1}^{N_2} \sigma\left( \sum_{j=1}^{N_1} W_{ij} v_j + c_i \right) \]

同様に、事後分布 \(p(\mathbf{v} \mid \mathbf{h}, \Theta)\) も次のように書ける。

\[ p(\mathbf{v} \mid \mathbf{h}, \Theta) = \prod_{i=1}^{N_1} p(v_i \mid \mathbf{h}, \Theta) = \prod_{i=1}^{N_1} \sigma\left( \sum_{j=1}^{N_2} W_{ji} h_j + b_i \right) \]

RBMでは、パラメータ \(\Theta = \{ \mathbf{W}, \mathbf{b}, \mathbf{c} \}\) に関する出力画像 \(\mathbf{v}\) の事後確率 \(p(\mathbf{v} \mid \Theta)\) を考え、この事後確率が真の確率密度分布 \(q(\mathbf{v})\) に近づくように、パラメータ \(\Theta\) する問題を考える。

ここで、確率密度分布同士の近さを図るために、次のKulback-Leiblerダイバージェンス (KLダイバージェンス)を導入する。

(9.8)\[\begin{split} \begin{align*} D_\text{KL}\left(q(\mathbf{v}) \mid\mid p(\mathbf{v} \mid \Theta) \right) &= \sum_{\mathbf{v}} q(\mathbf{v}) \log \frac{q(\mathbf{v})}{p(\mathbf{v} \mid \Theta)} \\ &= \mathbb{E}_{\mathbf{v} \sim q(\mathbf{v})}\left[ \log q(\mathbf{v})\right] - \mathbb{E}_{\mathbf{v} \sim q(\mathbf{v})} \left[\log p(\mathbf{v} \mid \Theta) \right] \end{align*} \end{split}\]

ここで、最適化するパラメータ \(W_{ij}\), \(b_i\), \(c_i\) のいずれかを表す変数として \(\theta\) を使い、(9.8)を \(\theta\) で微分する。 (9.8)の第1項はパラメータ \(\theta\) に依存しないので、次のように書ける。

\[ \frac{\partial D_\text{KL}\left(q(\mathbf{v}) \mid\mid p(\mathbf{v} \mid \Theta) \right)}{\partial \theta} = - \mathbb{E}_{\mathbf{v} \sim q(\mathbf{v})}\left[ \frac{\partial \log p(\mathbf{v} \mid \Theta)}{\partial \theta} \right] \]

これに (9.6) を代入して式を整理したい。まず、 (9.6) を周辺化して変数 \(\mathbf{h}\) を消去する。

(9.9)\[ p(\mathbf{v} \mid \Theta) = \sum_{\mathbf{h}} p(\mathbf{v}, \mathbf{h}) = \frac{1}{Z(\Theta)} \sum_{\mathbf{h}} \exp\left( -E(\mathbf{v}, \mathbf{h} \mid \Theta) \right) \]

(9.8)に、(9.9)と(9.7)を代入すると、次の式が得られる。

(9.10)\[\begin{split} \begin{align*} \frac{\partial D_\text{KL}\left(q(\mathbf{v}) \mid\mid p(\mathbf{v} \mid \Theta) \right)}{\partial \theta} &= - \mathbb{E}_{\mathbf{v} \sim q(\mathbf{v})}\left[ \frac{1}{\sum_{\mathbf{h}'} \exp\left( -E(\mathbf{v}, \mathbf{h}' \mid \Theta) \right)} \sum_{\mathbf{h}} \frac{\partial}{\partial\theta} \exp\left(-E(\mathbf{v}, \mathbf{h} \mid \Theta)\right) \right] \\ & \quad+ \sum_{\mathbf{v}, \mathbf{h}} \frac{\partial}{\partial \theta} \exp\left( - E(\mathbf{v}, \mathbf{h} \mid \Theta) \right) \\ &= \mathbb{E}_{\mathbf{v} \sim q(\mathbf{v})} \left[ \sum_{\mathbf{h}} \frac{\exp\left(-E(\mathbf{v}, \mathbf{h} \mid \Theta)\right)}{\sum_{\mathbf{h}'} \exp\left( -E(\mathbf{v}, \mathbf{h}') \right)} \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta} \right] \\ & \quad- \sum_{\mathbf{v}, \mathbf{h}} \frac{\exp \left( -E(\mathbf{v}, \mathbf{h} \mid \Theta) \right)}{\sum_{\mathbf{v}', \mathbf{h}'} \exp\left( -E(\mathbf{v}', \mathbf{h}') \right)} \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta} \\ &= \mathbb{E}_{\mathbf{v} \sim q(\mathbf{v}),~\mathbf{h} \sim p(\mathbf{h} \mid \mathbf{v}, \Theta)} \left[ \frac{\partial E(\mathbf{v}, \mathbf{h} \mid \Theta)}{\partial\Theta} \right] - \mathbb{E}_{\mathbf{v},~\mathbf{h} \sim p(\mathbf{v}, \mathbf{h} \mid \Theta)} \left[ \frac{\partial E(\mathbf{v}, \mathbf{h} \mid \Theta)}{\partial\Theta} \right] \end{align*} \end{split}\]

この式のようにKLダイバージェンスのパラメータ \(\theta\)に関する勾配が求まったら、あとは最急降下法の要領でパラメータを更新すればよいのだが、ここで一つ問題がある。それは第2項の期待値を解析的にも数値的にも計算することが困難、という点である。

この点を少し詳しく見ていこう。

まず、第1項は訓練データに含まれる画像を \(\mathbf{v}\) とすれば、\(q(\mathbf{v})\) は訓練データの分布そのものなので問題ない。また \(p(\mathbf{h} \mid \mathbf{v}, \Theta)\) についても、パラメータ \(\Theta\) が与えられれば、(9.4) を用いて計算できる。

従って、これらのサンプルに感する期待値は、訓練データからのサンプルを用いて計算可能である。

一方で、第2項の期待値計算のために用いる \(p(\mathbf{v}, \mathbf{h} \mid \Theta)\) を評価するには、任意の \(\mathbf{h}\) を考える必要があるため、この確率に関する期待値を求めるのは実質的に不可能である。

ここで、(9.6) の \(p(\mathbf{v}, \mathbf{h} \mid \Theta)\) の定義に話を戻そう。前述の通り、この定義では、\(\mathbf{v}\) 同士、または \(\mathbf{h}\) 同士の結合は存在せず、(9.4) と(9.5) を用いて 確率密度分布 \(p(\mathbf{h} \mid \mathbf{v}, \Theta)\) と \(p(\mathbf{v} \mid \mathbf{h}, \Theta)\) に従うサンプルを得ることはできる。

このようなケースでは、Gibbsサンプリングと呼ばれる手法をもちいて、 \(p(\mathbf{v}, \mathbf{h} \mid \Theta)\) に従うサンプルを近似的に取得することができる。Gibbsサンプリングの詳細については割愛するが、以下の操作によって、\(p(\mathbf{v}, \mathbf{h} \mid \Theta)\) に従うサンプルを得ることができる。

1. 可視層のニューロンの状態を \(\mathbf{v}\) として与える。

2. (9.4) を用いて、隠れ層のニューロンの状態 \(\mathbf{h}\) を計算する。

3. (9.5) を用いて、可視層のニューロンの状態 \(\mathbf{y}\) を計算する。

4. \(\mathbf{y}\) の値を \(\mathbf{v}\) として2.に戻る。

5. ある回数だけ3.と4.を繰り返す。

このようにして得られた \(\mathbf{v}\) と \(\mathbf{h}\) の組み合わせは、\(p(\mathbf{v}, \mathbf{h} \mid \Theta)\) に従うサンプルとなるので、これを用いて(9.10)の第2項の期待値を近似的に計算すれば良さそうだ。

通常、Gibbsサンプリングによって十分な数のサンプルを取得して(9.10)の第2項の期待値を求める必要がありそうだが、RBMではこのサンプリングを少ない回数 \(k\) 回だけ行って近似する。

このようにして得られたサンプルを用いた勾配の近似法を コントラストダイバージェンス法 (Contrastive Divergence, CD) と呼ぶ。興味深いことに、RBMの文脈では \(k = 1\) でも十分に良い学習が行えることが分かっている。

制限Boltzmannマシンに、先ほどと同様に0-9の数字を模した5×5のパターンを記憶させてみた結果が以下である。

以下の結果では、上の行にノイズ付の入力画像を、下の行に制限Boltzmannマシンによる出力画像を示した。

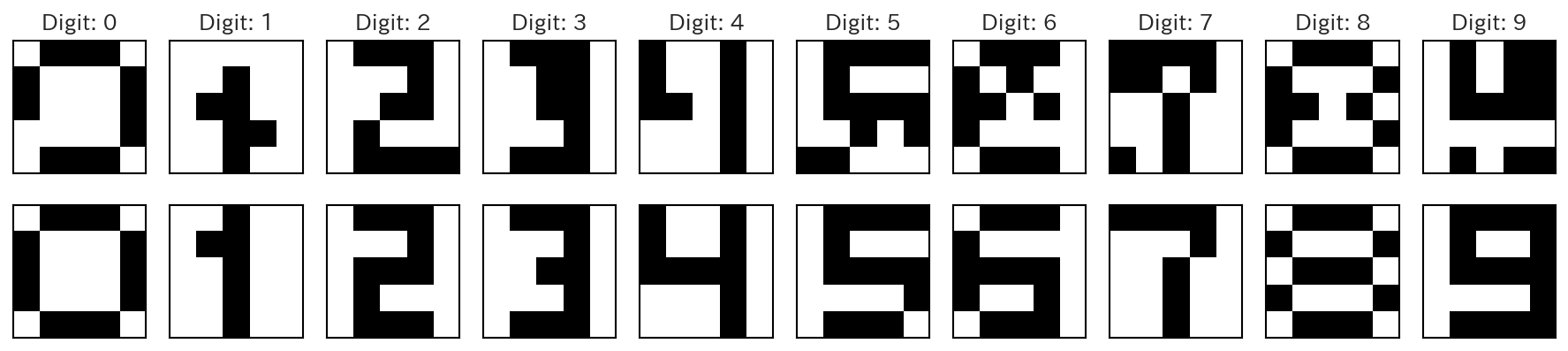
図 9.2 RBMによる画像の再構成結果

今回はスペースの都合上、学習した画像は示していないが、RBMが学習したパターンを完璧に再現できていることを付け加えておく。

これら、HopfieldネットワークやRBMの考え方が基礎となり、深層Boltzmannマシン (Deep Boltzmann Machine, DBM) や深層信念ネットワーク (Deep Belief Network, DBN) といった、より深い階層を持つニューラルネットの研究が行われ、今日の深層学習へと繋がっていく。

まとめ: 深層学習への歩み

• Hopfieldネットワークは、Hebb則に着想を得た連想記憶モデルである

• RBMは可視層と隠れ層からなり、その間の情報伝達を確率的に表現した連想記憶モデルである

• HopfieldネットワークやRBMは連想記憶のための古典的手法で、今日の深層学習の基礎を築いた

9.3. 深層学習モデルと画像認識

ここまでの流れのなかで発展した深層学習だが、初期の深層学習モデルはどのような構造だったのかを見ていこう。

本項ではまず、画像認識を主として提案された深層学習モデルについて見ていく (ただし、その用途を画像認識に限っているわけではない)。

9.3.1. LeNet-5

LeNet-5 は1998年にYann LeCunらが手書き数字認識のために開発した5層の階層的ニューラルネットである。

LeNet-5は複数の 畳み込み層 と プーリング層 を持ち、最後に全結合層を持つという今日の畳み込みニューラルネット (CNN)の典型的な構造を持つ。

しかし、この当時はプーリング層として平均プーリング (現在は最大プーリングが一般的)、活性化関数に双曲線余接 (tanh)関数 (現在はReLUが一般的)を使っているなど、今日の一般的なニューラルネットと異なる部分も多かった。

図 9.3 LeNet-5の構造 (c) CC BY-SA 4.0 Wikipedia Commons

LeNet-5の構造で興味深いのは、最後の全結合層が完全な全結合ではなく、ニューロン間の結合の一部が断ち切られている点である。

この構造は今日で言うところのドロップアウトと似た考え方であり、過学習を防ぐために一部のニューロンの結合を制限しているのだと捉えられる。

9.3.2. AlexNet

AlexNetは、2012年にILSVRCで優勝した深層学習モデルである [35]。AlexNetは、LeNet-5を改良したもので、以下のような特徴を持つ。

• 5層の畳み込み層と3層の全結合層からなる (LeNet-5より層の数が多い)

• 活性化関数にReLUを採用

• 過学習を抑制するためにドロップアウトを採用

LeNet5から10年以上の時を経て提案されたAlexNetは、これらの現在では一般的になっている多くの特徴を階層型ニューラルネットに取り込んでいる。

特に注目すべきは、これまでシグモイド関数は双曲線余接関数が一般的であった活性化関数に ReLU (rectified linear unit)を採用した点である。

ReLUは、入力が0以下のときは0を出力し、入力が0より大きいときはそのまま出力するという単純な関数であるが、シグモイド関数を用いる場合に問題であった 勾配消失 を防ぐことができる。

シグモイド関数は、入力の値の絶対値が大きい場合にその微分の値がほとんど0になる。数学的には、それほど問題には思えないかもしれないが、有限の解像度でしか数値を表現できないコンピュータにとっては、この小さな差が致命的なのである。すなわち、誤差逆伝播の過程において、シグモイド関数の微分が何度も掛け合わされると、最終的に勾配がほとんど0になってしまい、パラメータの更新が行われなくなってしまうのである。

一方で、ReLUの微分は言うまでもなく0か1のいずれかであるため、勾配消失の問題は起こらない。これにより、AlexNetは、より深い階層を持つニューラルネットの学習に成功した。

9.3.3. より大規模な畳み込みニューラルネット

AlexNet以降、VGG-16/19やGoogLeNet (Inception v3), ResNetなど、様々な深層学習モデルが提案された。

VGG-16/19 は、Visual Geometry Group (VGG)というオックスフォード大学の研究グループが提案したニューラルネットで、画像認識の性能改善のために、どのような構造が重要なのかを検討した結果を反映したものである。

VGGの研究では、AlexNetに用いられたLocal Response Normalization (LRN)が多層のニューラルネットでは、あまり効果がないことや、畳み込み層の数を増やせば増やすほど認識精度が向上することなどを示した。

しかし、19層からなるVGG-19よりも層を増やすと、性能が頭打ちになり、時には性能が低下することも分かった。そこで GoogLeNet では、層を枝分かれさせて、異なるサイズの畳み込みそうで特徴を抽出するInceptionモジュールを導入した。これによりGoogLeNetは22層のニューラルネットの学習を可能にした [37] 。

さらに、Microsoftの研究チームが発表したResNetは、残差学習と呼ばれる機構を用いて、実に50層以上の深いニューラルネットの学習に成功した [38]。

こうして、ニューラルネットは様々な工夫を得ながら層の数を増やすことで性能の向上を続けた。

9.3.4. Vision Transformer (ViT)

Vision Transformer (ViT)は、それまで自然言語処理の分野で広く用いられていたTransformerと呼ばれるニューラルネットワークを画像向けに改良したモデルである [39]。

ViTは、入力の画像を小さなパッチに分割し、各パッチからCNN等を用いて何らかの特徴ベクトルを抽出する。

最初の論文で提案されたViTは、画像を16×16のタイルに区切って、合計256個の画像パッチから特徴ベクトルを抽出しているのだが、各画像パッチをCNNに通さずに、単なる全結合層によって特徴ベクトルに変換している。

その後、抽出された特徴ベクトルを1つの配列上に並べて、Transformerに入力する。この際、オリジナルのTransformerと同様に、 位置エンコーディング (positional encoding) と呼ばれる手法を用いて、画像パッチの位置の情報を追加情報としてTransformerに与える。

その後、Transformerは、自己注意機構 (self attention module)を用いて、各パッチの特徴のうち、画像の認識に有効な特徴を強化するような操作を繰り返し行う。

このような操作を行うと、多層のCNNに比べて少ない層を持つTransformerであっても、十分な画像認識性能が得られることが実験的に示されている。

まとめ: 深層学習と画像認識

• 画像認識における深層学習モデルはLeNet-5を始めとして、畳み込みニューラルネットが主流となってきた

• AlexNet以降、徐々にニューラルネットの層の数を増やすことで認識精度を高めてきた

• 今日では、Vision Transformer (ViT)のように、CNN以外のニューラルネットにも注目が集まっている

9.4. 生成のための深層学習

深層学習が現れるまで、画像を1から生み出すような人工知能を作ることは難しく、生成に近いタスクとしては、前述の制限Boltzmannマシンのように画像を記憶するようなモデルが主流であった。

しかし、よく考えてみると、生成、というのは多くの画像を記憶して、それらを組み合わせて新しい画像を作る操作であり、記憶と生成には一定の関連性がある。

9.4.1. 変分オートエンコーダ (VAE)

変分オートエンコーダ (Variational Autoencoder, VAE)は、自己符号化器 (autoencoder)の拡張で画像を生成するためのニューラルネットである [40]。

VAEを理解するうえで大事な考え方に Evidence Lower Bound (ELBO)がある。VAEの説明に入る前に、まずはELBOの考え方について説明しよう。

当然ながら、画像生成のためのニューラルネットは画像データセット \(\mathcal{X} = \{ \mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_N \}\)を用いて訓練される。ここで、各画像がサンプルされる確率を \(p_\text{data}(\mathbf{x})\) とすると、画像生成は対数尤度の期待値

\[ \mathbb{E}_{\mathbf{x} \sim p_\text{data}} \left[ \log p_\theta(\mathbf{x}) \right] = \int p_\text{data}(\mathbf{x}) \log p_\theta(\mathbf{x}) d\mathbf{x} \]

をニューラルネットのパラメータ \(\theta\) について最大化する問題であると考えられる。ここで、生成される画像を説明する変数として潜在変数 \(\mathbf{z}\) を導入すると、Bayesの定理より、次の式が得られる。

(9.11)\[ p_\theta(\mathbf{x}) = \int p(\mathbf{x}, \mathbf{z}) \mathrm{d} \mathbf{z} = \int p_\theta(\mathbf{x} | \mathbf{z}) p(\mathbf{z}) \mathrm{d} \mathbf{z} \]

通常、潜在変数 \(\mathbf{z}\) は、多変量正規分布のような解析的にサンプル可能な分布に従うと仮定するので、 \(p(\mathbf{z})\)はパラメータ \(\theta\) に依存せず、簡単に計算できる。

しかし、(9.11) を解析的に計算することはできず、また、数値的に計算することも、次元の呪いの影響があり、通常は不可能である。

そこで、変分Bayes (variational Bayes)と呼ばれる手法を用いて、この積分の下界を近似的に求めることを考える。

変分Bayesでは、近似分布 \(q_\phi (\mathbf{z} | \mathbf{x})\) を導入し、次のような式を考える。

(9.12)\[\begin{split} \begin{align*} \log p_\theta(\mathbf{x}) &= \log \int p_\theta(\mathbf{x} | \mathbf{z}) p(\mathbf{z}) \mathrm{d} \mathbf{z} \\ &= \log \int \frac{q_\phi(\mathbf{z} | \mathbf{x})}{q_\phi(\mathbf{z} | \mathbf{x})} p_\theta(\mathbf{x} | \mathbf{z}) p(\mathbf{z}) \mathrm{d} \mathbf{z} \\ &= \log \int \frac{p_\theta(\mathbf{x} | \mathbf{z}) p(\mathbf{z})}{q_\phi(\mathbf{z} | \mathbf{x})} q_\phi(\mathbf{z} | \mathbf{x}) \mathrm{d} \mathbf{z} \\ &= \log \mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z} | \mathbf{x})} \left[ \frac{p_\theta(\mathbf{x} | \mathbf{z}) p(\mathbf{z})}{q_\phi(\mathbf{z} | \mathbf{x})} \right] \\ \end{align*} \end{split}\]

この式には何らかの関数の平均の対数を取る、という操作が含まれている。ここでJensenの不等式と呼ばれる次の不等式を用いる。

Jensenの不等式

とある確率変数 \(X\) と下に凸の関数 \(f\) について、次の不等式をJensenの不等式と呼ぶ。

\[ f(\mathbb{E}[X]) \leq \mathbb{E}[f(X)] \]

逆に \(f\) が上に凸の関数であるときは次式が成り立つ。

\[ f(\mathbb{E}[X]) \geq \mathbb{E}[f(X)] \]

対数関数は上に凸の関数であるため、Jensenの不等式を用いると、(9.12)は次のように書き直せる。

(9.13)\[\begin{split} \begin{align*} \log p_\theta(\mathbf{x}) &\geq \mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z} | \mathbf{x})} \left[ \log \frac{p_\theta(\mathbf{x} | \mathbf{z}) p(\mathbf{z})}{q_\phi(\mathbf{z} | \mathbf{x})} \right] \\ &= \mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z} | \mathbf{x})} \left[ \log p_\theta(\mathbf{x} | \mathbf{z}) \right] - D_\text{KL}(q_\phi(\mathbf{z} | \mathbf{x}) || p(\mathbf{z})) \\ \end{align*} \end{split}\]

ただし、式中の \(D_\text{KL}(q_\phi(\mathbf{z} | \mathbf{x}) || p(\mathbf{z}))\) は、Kullback-Leiblerダイバージェンスと呼ばれる、2つの確率分布の差を表す指標で、

\[ D_\text{KL}(q_\phi(\mathbf{z} | \mathbf{x}) || p(\mathbf{z})) = \int q_\phi(\mathbf{z} | \mathbf{x}) \log \frac{q_\phi(\mathbf{z} | \mathbf{x})}{p(\mathbf{z})} d\mathbf{z} \]

のように定義される。

(9.13) の右辺が、ELBOであり、ELBOが周辺対数尤度の下界を与えていることが分かる。従ってELBOを最大化することで、周辺対数尤度についてもより大きな値を得ることができる。

VAEの概要

VAEが考えるのはELBOの最大化そのものである。すなわち、VAEを訓練するための損失関数は次のように定義される。

(9.14)\[ \mathcal{L}(\mathbf{x}; \theta, \phi) = - \mathbb{E}_{\mathbf{x} \sim p_\text{data}} \left[ \log p_\theta(\mathbf{x}) \right] + D_\text{KL}(q_\phi(\mathbf{z} | \mathbf{x}) || p(\mathbf{z})) \]

VAEは自己符号化器 (autoencoder)の一種であるので、ニューラルネットはエンコーダとデコーダによって構成される。損失関数に含まれる2つの確率密度分布 \(p_\theta(\mathbf{x})\) と \(q_\phi(\mathbf{z} | \mathbf{x})\) はそれぞれ、エンコーダとデコーダの処理に対応している。

ここで、エンコーダは入力の画像 \(\mathbf{x}\) を受け取り、潜在変数 \(\mathbf{z}\) を出力するようなニューラルネットであって、 \(q_\phi(\mathbf{z} | \mathbf{x})\) からのサンプリングを担う。一方、デコーダは潜在変数 \(\mathbf{z}\) を受け取り、画像 \(\mathbf{x}\) を出力するようなニューラルネットであって、 \(p_\theta(\mathbf{x} | \mathbf{z})\) からのサンプリングを担う。

さて、\(\mathbf{z}\) が多変量正規分布 (もしくは他の解析的にサンプリング可能な分布)に従うと仮定したことを思い出してほしい。この条件を満たすために、エンコーダは直接 \(\mathbf{z}\) を出力する代わりに、多変量正規分布の平均 \(\boldsymbol{\mu}\) と分散 \(\boldsymbol{\sigma}^2\) を出力するように設計される。

図 9.4 変分オートエンコーダ (VAE)の構造

結局、(9.14) の第一項は、エンコーダに渡された画像 \(\mathbf{x}\) とデコーダからの出力 \(\mathbf{x}'\) の間の誤差を用いて近似され、第二項はエンコーダが出力する平均 \(\boldsymbol{\mu}\) と分散 \(\boldsymbol{\sigma}\) を持つ正規分布と \(p(\mathbf{z})\)として仮定した標準正規分布との間のKLダイバージェンスによって定義される。

9.4.2. 敵対的生成ネットワーク (GAN)

GANは、画像を生成する生成器 (generator)と、画像がデータセットに含まれる真の画像なのか、生成器によって作られた仮の画像なのかを見破る判別器 (discriminator)の2つニューラルネットにより構成される画像生成ためのニューラルネットである []。

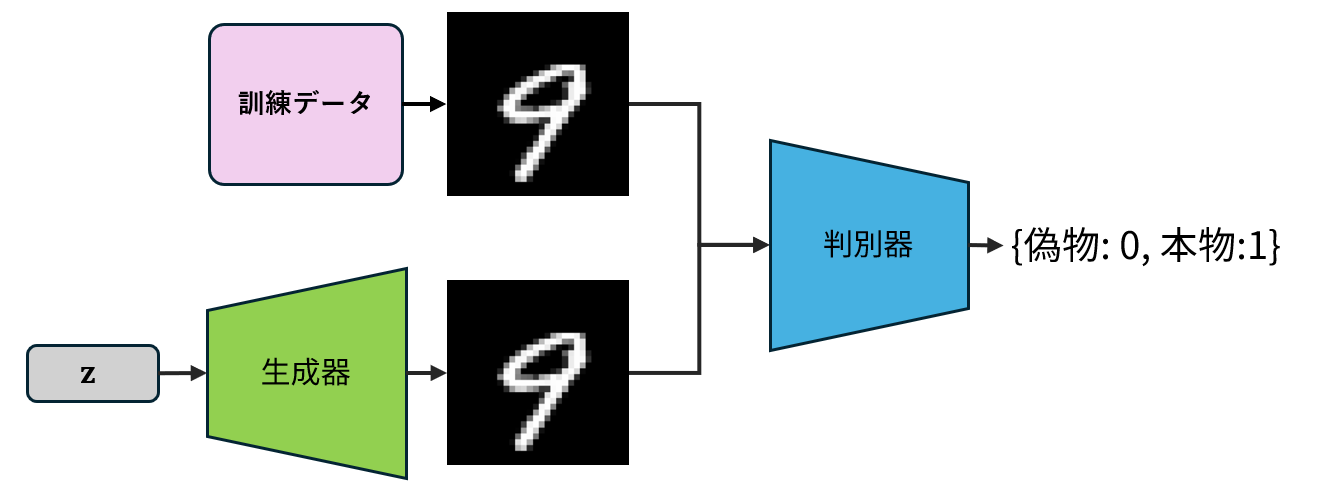
図 9.5 敵対的生成ネットワーク (GAN)の構造

Ian Goodfellowにより提案されたオリジナルのGANは、必ずしも深層学習を用いる手法ではなかったため、GANのうち、深層学習を用いるものを区別してDCGAN (Deep Convolutional GAN)と呼ぶこともある [41]。

GANが、より高品質な画像を生成できるようになる学習の過程は、偽札を作る犯罪者と、それを見破る警察との関係に例えられる。

すなわち、生成器は「判別器が本物と勘違いするような画像の生成」を目指し、判別器は「本物の画像と生成器が作った画像を見分けること」を目指して学習を行う。

この学習は、数学的には次のミニマックス関数の最適化問題として定式化される。

(9.15)\[ \min_G \max_D \mathbb{E}_{\mathbf{x} \sim p_\text{data}} \left[ \log D(\mathbf{x}) \right] + \mathbb{E}_{\mathbf{z} \sim p_\mathbf{z}} \left[ \log (1 - D(G(\mathbf{z}))) \right] \]

この式が一体何を意味するのかもう少し詳しく見ていこう。

GANが目指すもの

GANが最終的に達成したいのは、生成器により画像を生成する操作を、とある確率密度分布 \(p_G\) からのサンプリングに見立てた時に、この分布がデータの分布と一致する、すなわち \(p_G = p_\text{data}\) となることである。

GANの論文では、(9.15) の最適化が、2つの確率密度分布の差として、Jensen-Shannonダイバージェンスを最小化する問題と同義であることが述べられている。

Jensen-Shannon ダイバージェンス

Jensen-Shannonダイバージェンスは、2つの確率分布 \(p\) と \(q\) の間の距離を測る指標で、次のように定義される。

\[ D_\text{JS}(p, q) = \frac{1}{2} D_\text{KL}(p || m) + \frac{1}{2} D_\text{KL}(q || m) \]

ただし、 \(m\) は確率密度 \(p\) と \(q\) の混合分布で \(m = (p + q) / 2\) である。

GANが目指す「Jensen-Shannonダイバージェンスの最小化」について順に見ていこう。

まず初めに、「理想的な判別器」について考える。理想的な判別器は、任意の生成器 \(G\) に対して次の量 \(V(G, D)\) を最大化することを目指す。

\[\begin{split} \begin{align*} V(G, D) &= \int p_\text{data}(\mathbf{x}) \log D(\mathbf{x}) \mathrm{d}\mathbf{x} + \int p_\mathbf{z}(\mathbf{z}) \log (1 - D(G(\mathbf{z}))) \mathrm{d}\mathbf{z} \\ &= \int p_\text{data}(\mathbf{x}) \log D(\mathbf{x}) + p_G(\mathbf{x}) \log(1 - D(\mathbf{x})) \mathrm{d}\mathbf{x} \end{align*} \end{split}\]

この式は、交差エントロピーのような式になっていて、\(V(G, D)\)を最大化すると、第一項は \(p_\text{data}\) が高い確率を取る箇所では \(D\)が1に近い値を、\(p_\mathbf{z}\)が高い確率を取る箇所では \(D\) が0に近い値を取るようなる。

通常、\(a, b \in \mathbb{R}\)が \(a \neq 0\), \(b \neq 0\)を満たすとすると、 \(a \log y + b \log (1 - y)\) は \(y \in [0, 1]\) の範囲で \(y = \frac{a}{a + b}\)で最大値を取る。

従って、最適な判別器 \(D_G^{*}\) は任意の画像 \(\mathbf{x}\) について

\[ D_G^{*} = \frac{p_\text{data}(\mathbf{x})}{p_\text{data}(\mathbf{x}) + p_G(\mathbf{x})} \]

を満たす。

任意の \(G\)について、最適な\(D_G^{*}\) を与えることができたので、(9.15) を \(G\) に関する指標として \(C(G)\) と書くことにすると、\(C(G)\) は、次のような式で与えられる。

\[\begin{split} \begin{align*} C(G) &= \mathbb{E}_{\mathbf{x} \sim p_\text{data}} \left[ \log D_G^{*}(\mathbf{x}) \right] + \mathbb{E}_{\mathbf{z} \sim p_\text{noise}} \left[ \log (1 - D_{G}^{*}(G(\mathbf{z}))) \right] \\ &= \mathbb{E}_{\mathbf{x} \sim p_\text{data}} \left[ \log D_G^{*}(\mathbf{x}) \right] + \mathbb{E}_{\mathbf{x} \sim p_G} \left[ \log (1 - D_{G}^{*}(\mathbf{x})) \right] \\ &= \mathbb{E}_{\mathbf{x} \sim p_\text{data}} \left[ \log \frac{p_\text{data}(\mathbf{x})}{p_\text{data}(\mathbf{x}) + p_G(\mathbf{x})} \right] + \mathbb{E}_{\mathbf{x} \sim p_G} \left[ \log \frac{p_G(\mathbf{x})}{p_\text{data}(\mathbf{x}) + p_G(\mathbf{x})} \right] \end{align*} \end{split}\]

ここで、

\[\begin{split} \begin{align*} \mathbb{E}_{\mathbf{x} \sim p_\text{data}} \left[ \log \frac{p_\text{data}(\mathbf{x})}{p_\text{data}(\mathbf{x}) + p_G(\mathbf{x})} \right] &= \mathbb{E}_{\mathbf{x} \sim p_\text{data}} \left[ \log \frac{1}{2} + \log \frac{p_\text{data}(\mathbf{x})}{\frac{p_\text{data}(\mathbf{x}) p_G(\mathbf{x})}{2}} \right] \\ &= - \log 2 + D_\text{KL} \bigg( p_\text{data} \bigg\| \frac{p_\text{data} + p_G}{2} \bigg) \end{align*} \end{split}\]

であって、同様に \(\mathbb{E}_{\mathbf{x} \sim p_G}\) も書き直せるので、結局、\(C(G)\) は次のように書ける。

\[\begin{split} \begin{align*} C(G) &= -\log 4 + D_\text{KL} \bigg( p_\text{data} \bigg\| \frac{p_\text{data} + p_G}{2} \bigg) + D_\text{KL} \bigg( p_G \bigg\| \frac{p_\text{data} + p_G}{2} \bigg) \\ &= -\log 4 + 2 D_{JS} (p_\text{data} || p_G) \end{align*} \end{split}\]

Jensen-Shannonダイバージェンスは \(p_\text{data} = p_G\) のときに最小の0を取る。

以上から、(9.15) を最適化する操作は、\(p_\text{data}\) と \(p_G\) の間のJensen-Shannonダイバージェンスを最小化する操作と同等であることが確認できた。

モード崩壊

GANの画像生成の過程は偽札を作る犯罪者と、それを見破る警察の関係に例えられると、本節の冒頭で述べた。

しかし、あなた自身が偽札を作る犯罪者だとして、日本で言うところの1000円札、5000円札、10000円札の全ての偽札を作りたいと思うだろうか？当然、本当に作りたいのは10000円札だけだろう。

このことと同様の問題がGANにも発生する。GANの生成器は、判別器に見破られない画像を作るために、自分の得意な画像だけを生成すれば十分なのである。そのため、GANの生成画像は、元の画像データセット全体を模倣するのではなく、その一部だけを模倣するようになってしまう。

このように似たような画像ばかりが生成されてしまう問題を モード崩壊 (mode collapse)と呼ぶ。

モード崩壊はGANの中心的な課題として、いくつもの研究で解決が試みられてきた。例えば、Wasserstein GAN (WGAN) [42] [43] や、Spectral Normalization[44]などの手法により、モード崩壊が緩和できるとされている。

9.4.3. 拡散モデル

拡散モデル (diffusion model)は、2020年台に登場した新しいタイプの生成モデル[45]で、非常に高精細な画像を生成できることで注目を集めている。

拡散モデルのポイントは、ある画像に徐々にノイズを加えていくと、最終的には完全なノイズ画像と見分けがつかないような画像になる、という点にある。

図 9.6 MNISTの数字画像にノイズを付加する様子

そこで反対に、完全なノイズ画像から徐々にノイズを取り払っていけば、鮮明な画像が得られそうだ。このアイディアに基づき、拡散モデルでは、ノイズを少しだけ取り払う操作をニューラルネットで行い、完全なノイズ画像を徐々に生成画像に近づけていく。

しかし、弱いノイズを付加して、完全なノイズ画像と見分けがつかないような画像を得るには、非常に多くのステップが必要になる。

従って、その反対の操作、すなわち完全なノイズ画像から徐々にノイズを取り払う操作にも非常に多くのステップが必要になる。

そのため、安直に考えると、完全な画像から数百回のステップでノイズを徐々に取り払って得られた画像が、訓練データに含まれる画像にするように学習することは非常に困難に思える。

しかし、拡散モデルは、その過程を理論的にうまく定式化しており、ニューラルネットの訓練時には、 数百のステップのうちの1ステップ分に相当するノイズ除去の処理だけを学習すれば良い。

9.4.4. マルチモーダル生成

近年では、OpenAIのDALL-E (URL) やGoogleのImagen (URL), Stability AIのStable Diffusion (URL)など、テキストから画像を生成する マルチモーダル生成モデルが注目を集めている。

ここでは、論文として公開されている情報から、これらのテキストに基づく画像生成モデルを簡単に紹介しよう。

DALL-E

OpenAIが、2021年の2月に公開したテキストから画像を生成するモデルが DALL-E で、そのおおよその内容は [46]にまとめられている。

オリジナルのDALL-Eの目的はTransformerを用いたテキストのエンコードと、それに基づいた画像の生成であると論文に述べられており、DALL-Eはエンコーダ部とデコーダ部にそれぞれTransformerを用いたVAEのような構造を持つ。著者らはこの構造のことをdVAE (discrete VAE) と呼んでいる。

このdVAEは、VAEの仲間の中で比較的高品質な画像を生成できるVector-Quantized VAE (VQ-VAE) [47]と類似しており、画像から得られた特徴ベクトルをベクトル量子化によって得られたコードブックにより離散的なトークンの情報へと変換する。

得られた画像のトークンはテキストから抽出されたトークンと結合後に、Transformerベースのデコーダへと渡されて、最終的な出力画像が得られる

DALL-Eの後継モデルである DALL-E 2 は、DALL-Eの公開からおよそ1年後の2022年4月に公開されてたモデルで、いくつかの改善が取り入れられている[48]。

その中でも注目すべきなのは、組になった画像情報とテキスト情報に類似した潜在ベクトルを与えるCLIP (Contrastive Language-Image Pretraining)を利用している点だろう。

DALL-E 2では、入力のテキスト情報からCLIPを用いて「言語的な潜在ベクトル」を得た後、それを「画像的な潜在ベクトル」へと変換する処理を行う。

その後、得られた画像的な潜在ベクトルは、GLIDE [49] (Generative Language-Image Diffusion for Editing)と呼ばれる拡散モデルに入力され、最終的な画像が得られる。

Imagen

Imagenは、DALL-E 2の公開からおよそ1ヶ月後の2022年5月にGoogleが公開したマルチモーダルモデルである [50]。

Imagenは、DALL-E 2のように、すでに画像とテキストが関係づけられているCLIPのようなモデルを利用せず、T5-XXLという大規模な言語モデル (ただし、今では中規模程度かもしれない)を使ってテキストから特徴を抽出する。

あとは、拡散モデルが、ノイズ画像から画像を復元する過程で、テキストから得られた特徴ベクトルを条件として与えることで、テキストに沿った画像を生成する。

Imagenは、テキストに沿った画像を生成するために、 Classifier-Free Guidance (CFG)と呼ばれる手法を用いており、これにより、画像生成時には、どの程度テキストに沿った画像を生成するかを調整できる。

また、Imagenは最初に解像度の小さな画像を生成したあとに、その解像度を拡散モデルを用いて徐々に大きくするという方式を取っており、必要に応じて高解像度画像の生成が可能になっている。

9.4.5. Stable Diffusion

これら3つのモデルの中で最も知名度が高いであろう Stable Diffusion は、2022年8月にStability AIが公開したマルチモーダル生成モデルである。

Stable DiffusionはDALL-E 2とImagenの両方の特徴を持ったモデルで、テキストからの特徴抽出と、画像生成のそれぞれにおいて、従来モデルの優れた点を取り入れている。

まず、テキストからの特徴抽出には、DALL-E 2と同様に事前学習済みのCLIPを利用する。このCLIP特徴は、Imagenと同様にCFGの枠組みで画像生成を担当する拡散モデルに渡される。

しかし、Stable Diffusionが、従来のモデルと最も異なっている点は、潜在空拡散 [51]と呼ばれる技術により、拡散モデルの計算量の問題を解決している点である。

潜在空間拡散モデルは、学習済みのVAEを用いて得られる潜在ベクトルを拡散モデルを用いて再現する。この潜在ベクトルのための拡散モデルにおいて、テキスト特徴を用いたCFGによる条件付けが行われる。

また、Stable Diffusionは、他の2つのモデルと異なり、モデル自体がHugging Faceのようなプラットフォームで公開されており、誰でも利用できるようになっている。

それ故、Stable Diffusionは、それ以後の研究において、いわゆる基盤モデルとして、様々な応用に広く利用されている。

まとめ: 生成のための深層学習

• 画像生成は深層学習の出現により大きく進歩した分野でVAEやGAN、拡散モデルなど、複数の技術が提案されている

• VAEは変分Bayesの枠組みを用いて、変分限界 (ELBO)を最大化するようにニューラルネットを訓練する

• GANは、生成器と判別器の2つのニューラルネットを競わせる形で、より高品質の画像を生成・判別するように訓練する

• 拡散モデルは、ノイズを徐々に取り除く処理をニューラルネットに学習させることで、最終的に高品質の画像を生成する