7. 物体追跡

本節では、動画像中の移動物体を検出・追跡するための手法について紹介する。

移動物体の検出には、オプティカルフローと呼ばれる動きベクトルがよく用いられる。

また、物体の追跡には、Lukas-Kanade法やMean-Shift法などの様々な手法があり、代表的な手法を順に紹介する。

参考資料

• 『ディジタル画像処理 改訂第二版』 P.331 第14章 動画像処理

7.1. オプティカル・フロー

オプティカル・フロー検出の代表的なアルゴリズムには、ブロック・マッチング法と勾配法の2つがある。

ブロック・マッチング法は2つの連続するフレームの間で、画像パッチの類似度を基にパッチの次の位置を推定する手法である。しかし、ブロック・マッチング法は、物体の動きが大きい場合にも利用できるが、その反面、画像パッチ同士の類似度計算に多くの計算時間を要する。

勾配法は、動画のように、連続するフレーム間の時間差が微小であると仮定できる場合に有効な手法で、以下では、勾配法を中心に、その原理を説明する。

7.1.1. 勾配法の基本

動画像は画像の \((x, y)\) における画素値が時間 \(t\) によって変化する関数 \(I(x, y, t)\) であると考えられる。この画素値が時間 \(\Delta t\) の間に、 \((\Delta x, \Delta y)\) だけ移動したとすると、次の等式が成り立つ。

(7.1)\[ I(x, y, t) = I(x + \Delta x, y + \Delta y, t + \Delta t) \]

この式の右辺を1次Taylor展開すると、次のように書ける。

(7.2)\[ I(x + \Delta x, y + \Delta y, t + \Delta t) = I(x, y, t) + \frac{\partial I}{\partial x} \Delta x + \frac{\partial I}{\partial y} \Delta y + \frac{\partial I}{\partial t} \Delta t \]

従って、 (7.1) と (7.2) から、次の等式が得られる。

\[ \frac{\partial I}{\partial x} \frac{\Delta x}{\Delta t} + \frac{\partial I}{\partial y} \frac{\Delta y}{\Delta t} + \frac{\partial I}{\partial t} = 0 \]

求めるべきオプティカル・フローは \((u, v) = (\Delta x / \Delta t, \Delta y / \Delta t)\) であるので、画像の\(x\), \(y\), \(t\)方向の勾配をそれぞれ \(I_x\), \(I_y\), \(I_t\) と書くことにすると、以下の式が得られる。

(7.3)\[ I_x u + I_y v + I_t = 0 \]

この式は、オプティカル・フローが満たすべき基本的な制約条件であり、 オプティカル・フローの拘束方程式 (optical flow constraint equation) とも呼ばれる。

しかし、この拘束方程式は未知数を \((u, v)\) の2つ持つので、この式を画素ごとに解くことはできない。そこで、いくつかの仮定を導入して \((u, v)\) を求める必要がある。

7.1.2. Lucas-Kanade法

Lucas-Kanade法は、勾配法によるオプティカル・フロー検出の代表的な手法で、1981年にBruce LucasとTakeo Kanadeによって提案された [27]。

この手法では、とある注目画素の近傍では同じオプティカル・フロー \((u, v)\) が得られると仮定して、(7.3) を解く。近傍に含まれる画素値を \((I_{x,1}, I_{y,1}, I_{t,1}), (I_{x,2}, I_{y,2}, I_{t,2}), \ldots, (I_{x,n}, I_{y,n}, I_{t,n})\) のように表すこととすると、(7.3) は次のような連立方程式で書き直せる。

\[\begin{split} \begin{pmatrix} I_{x,1} & I_{y,1} \\ I_{x,2} & I_{y,2} \\ \vdots & \vdots \\ I_{x,n} & I_{y,n} \end{pmatrix} \begin{pmatrix} u \\ v \end{pmatrix} = \begin{pmatrix} -I_{t,1} \\ -I_{t,2} \\ \vdots \\ -I_{t,n} \end{pmatrix} \end{split}\]

この連立方程式は、一般に過剰拘束な方程式になっているので、最小二乗法の枠組みによって \((u, v)\) を求めることができる。すなわち \(\mathbf{f} = (u, v)\) は次のように計算される。

\[ \mathbf{f} = -\begin{pmatrix} \mathbf{A}^T \mathbf{A} \end{pmatrix}^{-1} \mathbf{A}^T \mathbf{b} \]

ただし、\(\mathbf{A}\), \(\mathbf{b}\) は次のように定義される。

\[\begin{split} \mathbf{A} = \begin{pmatrix} I_{x,1} & I_{y,1} \\ I_{x,2} & I_{y,2} \\ \vdots & \vdots \\ I_{x,n} & I_{y,n} \end{pmatrix}, \quad \mathbf{b} = \begin{pmatrix} I_{t,1} \\ I_{t,2} \\ \vdots \\ I_{t,n} \end{pmatrix} \end{split}\]

Lucas-Kanade法は、各画素ごとに、比較的小さな連立方程式を解くだけで良いので、計算量も少なく、実装も容易である。

7.1.3. アパチャ―問題

Lucas-Kanade法のような局所情報に基づくオプティカル・フロー検出法の欠点の一つに、アパチャ―問題 (aperture problem) と呼ばれる問題がある。

アパチャ―問題は、小さな除き穴から、物体が移動する様子を観察したときに起こる動きの曖昧さに関する問題である。例えば、円形の窓の中で横方向に引かれた直線が上から下に移動するようなケースを考えよう。この場合、窓の中に見える情報だけを頼りにすれば、物体は単純に上から下に動いたと考えられる。

しかし、直線のように見えていたものが実は長方形の一辺を表す線分だったとしよう。この場合、長方形が実は斜め上方向に移動していたとしても、窓の中に見える情報だけから、横方向の動きを知ることはできない。もし、正しく長方形の動きを検出しようとするなら、長方形の一部だけでなく、全体を観察する必要があるのである。

このように、局所情報だけでは、物体の実際の動きを知ることはできない場合があり、Lucas-Kanade法も、アパチャ―問題により、正確なオプティカル・フローを検出できない場合がある。

Lucas-Kanade法において、アパチャ―問題を緩和する方法に、画像ピラミッドを用いる方法がある [28]。画像ピラミッドは、元の画像を様々な解像度に変換した画像の集合である。

画像ピラミッドを用いると、より低解像度の画像では広い範囲の情報を考慮したフローを計算できる。より具体的には、画像ピラミッド上の低解像度画像から順にLucas-Kanade法を適用し、得られたフローを高解像度画像に伝播していくことで入力の画像解像度に相当するオプティカル・フローを計算する。

7.1.4. Horn-Schunck法

Horn-Schunck法は、勾配法に基づくオプティカル・フロー検出の別手法で、Lucas-Kanade法と同年の1981年にBerthold K. P. HornとBoris G. Schunckによって提案された [29]。

こちらも、Lucas-Kanade法と同様にオプティカル・フローが近傍の画素では近い値になるはずである、という仮定を用いるが、Lucas-Kanade法とは対象的に、画像全体に対して定義される以下のエネルギー関数を用いる。

(7.4)\[ E = \sum_{x, y} \left( I_x u + I_y v + I_t \right)^2 + \lambda \sum_{x, y} \left( u_x^2 + u_y^2 + v_x^2 + v_y^2 \right) \]

各画素のオプティカル・フローは、このエネルギーを最小化することで求められる。

Euler-Lagrange方程式との関係

(7.4) を \(x\), \(y\) に関する積分式で書き表すと、次のようになる。

\[ E = \iint \left( I_x u + I_y v + I_t \right)^2 + \lambda \left( \left\| \nabla u \right\|^2 + \left\| \nabla v \right\|^2 \right) \mathrm{d} x \mathrm{d}y \]

このエネルギー関数において変数である \(u\) と \(v\) は、それ自体が \(x\), \(y\) の関数であるので、エネルギーを最小化するために、単純な微分を用いることはできない。ここで、関数 \(u\) と \(v\) が、微妙に変化したとしても、エネルギーが変化しないような状態を考える必要がある。このような状態のことを 定常状態 (stationary state) と呼ぶ。また、定常状態を求めるための、関数によるエネルギー関数の変化を求める方法を「微分」と区別して 変分 (variation) と呼ぶ。

Euler-Lagrange方程式 は変分を用いた目的関数の最小化に関する方程式である。一般的な位置 \(x\), 速度 \(\dot{x}\), 時刻 \(t\) に関する関数 \(L(x, \dot{x}, t)\) (この関数をLagrangianと呼ぶ) に対して、作用とも呼ばれる以下の目的関数\(S\)は次のように定義される。

(7.5)\[ S = \int L(x, \dot{x}, t) \mathrm{d} t \]

ここで注目すべきポイントは、

• \(L\) の引数に含まれる \(x\) と \(\dot{x}\) の両方が \(t\) に依存している

• \(L\) が時刻 \(t\) について積分されている

ということである。この作用 \(S\) を最小化するような \(x\) の定常状態は次のEuler-Lagrange方程式を満たす。

\[ \frac{\mathrm{d}}{\mathrm{d} t} \left( \frac{\partial L}{\partial \dot{x}} \right) - \frac{\partial L}{\partial x} = 0 \]

この方程式はLagrangeの運動方程式とも呼ばれていて、 \(L\) の定義次第では物理学における運動方程式の一般化された形となる。

ここでHorn-Schunck法におけるエネルギー関数に話を戻そう。(7.4) は、\(u\) と \(v\) の関数に対するエネルギー関数なのであった。

このエネルギー関数には、 \(u\) と \(v\) そのものに加えて、 \(x\), \(y\) のそれぞれによる偏微分が含まれている。さらに、\(u\) と \(v\) はそれぞれ \(x\), \(y\) の関数であって、関数の定義に現れる積分は \(x\), \(y\) に関するものである。

以上の特徴を踏まえると、Horn-Schunck法のエネルギー関数は、(7.5) の多変数版であることが分かる。すなわち、Horn-Schunck法のエネルギー関数 \(E\) における被積分関数を

\[ L(u, v, u_x, u_y, v_x, v_y, x, y) = \left( I_x u + I_y v + I_t \right)^2 + \lambda \left( \left\| \nabla u \right\|^2 + \left\| \nabla v \right\|^2 \right) \]

と書くと、 \(E\) を最小化するような \(u\) と \(v\) の定常状態は次のEuler-Lagrange方程式を満たす。

(7.6)\[\begin{split} \begin{align*} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial L}{\partial u_x} + \frac{\mathrm{d}}{\mathrm{d}y} \frac{\partial L}{\partial u_y} - \frac{\partial L}{\partial u} &= 2 \lambda \left( u_{xx} + u_{yy} \right) - 2 \left( I_x u + I_y v + I_t \right) I_x = 0 \\ \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial L}{\partial v_x} + \frac{\mathrm{d}}{\mathrm{d}y} \frac{\partial L}{\partial v_y} - \frac{\partial L}{\partial v} &= 2 \lambda \left( v_{xx} + v_{yy} \right) - 2 \left( I_x u + I_y v + I_t \right) I_y = 0 \end{align*} \end{split}\]

さて、ここまで、わざとエネルギー関数 \(E\) を連続化してEuler-Lagrange方程式を導出するという流れで、オプティカル・フローが満たすべき偏微分方程式を導いたが、数学的な厳密性を多少犠牲にすれば、この方程式はもう少し簡単に導くことができる。

というのも、 (7.4) において差分表現を用いて \(u_x, u_y\) 等を表しておけば、単純な \(u\), \(v\) に関する「微分」を考えるだけで、 (7.6) と同様の方程式を導けるのである。

例えば \(u_x^2\) を前方差分と後方差分を用いて

\[ u_x^2 = (u(x + 1, y) - u(x, y))(u(x, y) - u(x - 1, y)) \]

のように書いたとすると、 \(u(x, y)\) に関する \(u_x^2\) の微分は

\[\begin{split} \begin{align*} \frac{\partial u_x^2}{\partial u} &= (u(x + 1, y) - u(x, y)) - (u(x, y) - u(x - 1, y)) \\ &= u(x + 1, y) - 2u(x, y) + u(x - 1, y) \\ &= u_{xx} \end{align*} \end{split}\]

のように書ける。同様の操作を \(u_y^2\), \(v_x^2\), \(v_y^2\) にも適用すると、 (7.6) と同様の式が得られることが分かるだろう。

よって、Horn-Schunck法を離散的な画像に対して適用する場合には、

\[\begin{split} \begin{align*} \Delta u &= 2 \lambda \left( u_{xx} + u_{yy} \right) - 2 \left( I_x u + I_y v + I_t \right) I_x = 0 \\ \Delta v &= 2 \lambda \left( v_{xx} + v_{yy} \right) - 2 \left( I_x u + I_y v + I_t \right) I_y = 0 \end{align*} \end{split}\]

のように更新量を定義して、最急降下法の要領で \(u\) と \(v\) を更新していけば良い。ただし、この勾配は、動画全体に対して定義される必要があり、この勾配を用いたフローの更新を何度も行う必要があることから、Horm-Schunck法は計算量が大きくなる傾向がある。

まとめ: オプティカル・フロー

• オプティカル・フローは、動画像中の物体の動きを表すベクトル場である。

• フロー計算の代表的な手法には、Lucas-Kanade法とHorn-Schunck法がある。

• Lucas-Kanade法は、近傍の画素情報だけを用いる手法で、実装も容易だが、アパチャー問題の影響を受けやすい。

• Horn-Schunck法は、画像全体の情報を用いる手法で、アパチャー問題の影響を受けにくいが、計算量が多くなる。

7.2. 物体追跡

ここまでに紹介したオプティカル・フローは、動画像内における物体の移動量を表すベクトル場であったが、これを実際の物体検出に用いるには、移動方向をヒントとしつつ、次のフレームにおいて対応する箇所をテンプレート・マッチング等を用いて検出する必要がある。

しかし、このような方法は、計算量が大きく、対応点を見つけようとする箇所が時間経過に応じて変化する可能性などを考慮できないために頑健性に欠ける。そこで、以下ではより実用的な方向として、いくつかの物体追跡に特化した手法を紹介する。

7.2.1. Kanade-Lucas-Tomasi (KLT) 法

Kanade-Lucas-Tomasi (KLT) 法は、提案者の名前をとって名付けられた物体追跡手法で、オプティカル・フロー計算のアルゴリズムであるLucas-Kanade法の考え方をCarlo Tomasiが拡張したものである [30]。

KLTトラッカーでは、2つの連続するフレーム \(I\) が\(J\) を考え、\(I\) における注目点 \(\mathbf{x}\) が \(J\) 上でどこに移動するかを考える。対応点を考えるにあたって、 \(\mathbf{x}\) の近傍を表す窓内に存在する画素の集合を \(\mathcal{W}\) と書くことする。また、窓内の各点の座標は窓の中心を原点とする座標で表現されているとしよう。

ここで、窓内の点 \(\mathbf{x} \in \mathcal{W}\) の移動はアフィン変換を用いて \(\mathbf{A} \mathbf{x} + \mathbf{d}\) に移動すると考える。

こうすることで、画像内の物体の向きが変化したり、カメラに対して近づいたり遠ざかったりする効果を考慮することができる。なお、各点の座標は窓の中心を原点としているので、ベクトル \(\mathbf{d}\) は窓の平行移動量を表す。

この表現を用いると、窓内の画素の画素値が満たすべき条件は

\[ I(\mathbf{x}) = J(\mathbf{A} \mathbf{x} + \mathbf{d}) \]

のように書けるので、これを最小化するような\(\mathbf{A}\) と \(\mathbf{d}\) を求めれば良い。

ただし、このままの式では少々扱いにくいので、実際の画素の移動量である

\[ \mathbf{A}\mathbf{x} + \mathbf{d} - \mathbf{x} \]

を考えるために、行列 \(\mathbf{A}\) を次のように定義する。

\[ \mathbf{A} = \mathbf{D} + \mathbf{I} \]

ここで \(\mathbf{I}\) は単位行列を表す。

さらに、 \(\mathbf{u} = \mathbf{D} \mathbf{x} + \mathbf{d}\) と書くと、 \(\mathbf{A} \mathbf{x} + \mathbf{d} = \mathbf{x} + \mathbf{u}\) と書き直せる。

すると \(\mathbf{u}\) が十分小さければ \(J\) を \(\mathbf{u}\) に関して、1次の項までTaylor展開することで次の近似式が得られる。

(7.7)\[\begin{split} \begin{align*} J(\mathbf{Ax} + \mathbf{d}) &= J(\mathbf{x} + \mathbf{u}) \\ &= J(\mathbf{x}) + \nabla J(\mathbf{x})^T \mathbf{u} \end{align*} \end{split}\]

以上をまとめると、窓 \(\mathcal{W}\) 内の画素の変換 \((\mathbf{D}, \mathbf{d})\) が満たすべき条件は次のようになる。

(7.8)\[ I(\mathbf{x}) = J(\mathbf{x}) + \nabla J(\mathbf{x})^T (\mathbf{D} \mathbf{x} + \mathbf{d}) \]

KLTトラッカーでは、 \(\mathbf{D}_0 = \mathbf{I}\), \(\mathbf{d}_0 = \mathbf{0}\) で初期化した上で、(7.8) を最小化するような \(\mathbf{D}\) と \(\mathbf{d}\) によって \(\mathbf{D}_i\) と \(\mathbf{d}_i\) を更新していく。

ここでは詳細を割愛するが、(7.8) を満たすような\(\mathbf{D}\) と \(\mathbf{d}\) は単純な6次元の連立方程式を解くだけで求めることができる。

ただし、(7.7)で \(\mathbf{u}\) が小さいことを仮定した近似を用いているので、実際には\(\mathbf{D}\) と \(\mathbf{d}\) を求めては、それを差分として更新するという処理を何度か繰り返す必要がある。

以上の処理に基づくKLTトラッカーは、全ての画素を追跡するのではなく、一定の条件を満たす特徴点だけを追跡するので十分高速に動作できる。

7.2.2. Mean-Shiftトラッキング

Mean-Shiftトラッキングは、追跡対象物体の色分布を用いて物体の移動量を求める手法である。

物体の色分布は、初期フレームにおいてユーザによって設定された関心領域 (ROI, region of interest) 内の画素の色をヒストグラム化して作成される。一例として、初期フレームの関心領域を次の画像のように設定したとしよう。

図 7.1 初期フレームと関心領域

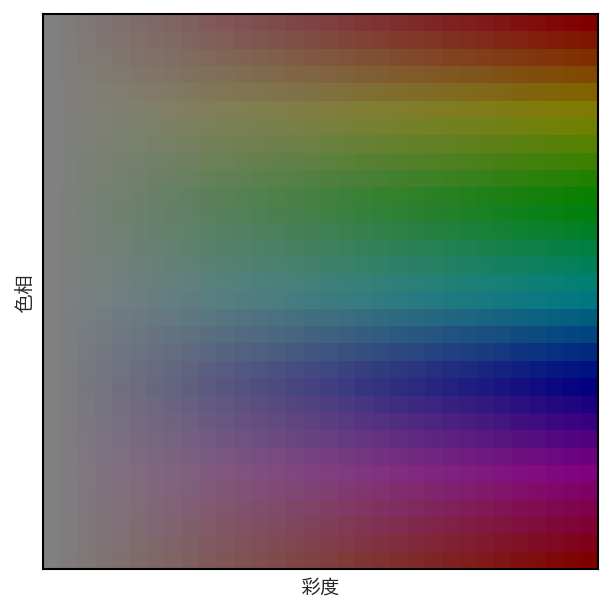
この関心領域内の画素が持つ色をヒストグラムに変換するのだが、RGB色情報を離散化するとヒストグラムのサイズが大きくなり、また、明るさの変化に影響されやすくなるので、RGB色空間の代わりにHSV色空間を用いることが多い。

カラー画像と色空間 で紹介したように、HSV色空間は、色相(Hue), 彩度(Saturation), 明度(Value) の3つの成分からなる色空間である。色相は色の種類を表し、彩度はその色の鮮やかさを表し、明度はその色の明るさを表す。

ヒストグラムを作成する場合には、H, S, Vの各成分をいくつかのビンで離散化する。例えば、Hの成分とSの成分だけに注目して、それぞれを32個のビンで離散化したとすると、以下の画像に示すような1024種類の色に対応するヒストグラムが計算できる。

さて、このようなビンをつかって先ほどの初期フレームの関心領域内の画素の色をヒストグラム化すると、以下のようなヒストグラムが得られる。

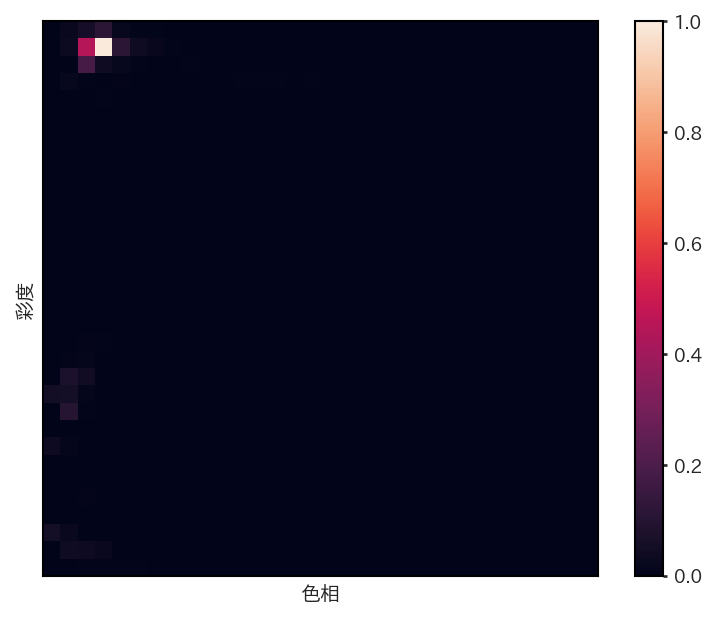
図 7.2 関心領域内の画素に対する色相と彩度の2次元ヒストグラム

このようなヒストグラムが得られたら、次のフレームの画像の各画像の画素について、「その画素が属するヒストグラムのビンの頻度」を画素値に持つ確率画像を作成する。

例えば、次のような画像を得ることができる。

図 7.3 確率画像の例

この確率画像を見てみると、物体が存在しそうな領域で大きな値を持っていることが確認できる。確率画像は、ブロック状の領域に分割され安い傾向があるので、実際に使用する際にはGaussianフィルタ等で平滑化すると良い。

確率画像が得られたら、前のフレームで得られている関心領域をMean-Shift法を用いて更新する。

Mean-Shift法は、

• 関心領域の矩形内に含まれる画素の位置を確率画像の値で重み付け平均して重心を求める

• 矩形の重心が新たに求められた重心に一致するように矩形を移動する

という操作を繰り返すことで、現在のフレームにおける関心領域を決定する。

このような確率画像の作成と、Mean-Shift法による関心領域の更新を繰り返すことで次の動画のような物体追跡が可能となる。

この結果から分かる通り、Mean-Shiftトラッキングによって、物体の移動をある程度追跡できている。しかし、やや関心領域の矩形の揺れが大きく、場合によっては追跡に失敗する可能性も多い。

7.2.3. Kalmanフィルタ

Kalmanフィルタは誤差を含むような観測情報から、誤差を含まない真の状態を推定するためのアルゴリズムである。KalmanフィルタはBayesianフィルタの一種で、Bayes推論に基づいて真の状態を予測する。

Kalmanフィルタ自体は非常に応用範囲の広い手法であるが、ここでは、動画像中の物体追跡に特化してKalmanフィルタの概要について説明する。この場合、Kalmanフィルタに入力される「誤差を含む観測情報」は別の物体追跡手法 (例えば、KLT法やMean-Shift法) によって取得する。

従って、Kalmanフィルタは、それ自体が物体追跡の手法というわけではなく、別の物体追跡手法と組み合わせて用いることで、より精度の高い物体追跡を実現するための手法であるといえる。

Kalmanフィルタの説明に入る前に、観測情報や状態といった言葉の意味について整理しておこう。 観測情報 とは何らかのセンサ等によって得られた観測対象の状態のことで、物体追跡に関して言えば、追跡対象物体の位置が観測情報にあたる。動画像から物体の位置を観測するには、例えばテンプレート・マッチングなどを使うことができるだろう。

状態 とは、通常、観測できる情報よりも多くの情報を含む、観測対象物体の様子を記述するパラメータを指す。物体追跡に関して言えば、物体の位置と速度を状態変数とすることが多い (もっと多くの情報を状態変数にとっても良い)。

観測方程式

以下では、単純な物体追跡のモデルとして、物体の位置と速度を含む状態 \(\mathbf{x}_t = (x_t, y_t, \dot{x}_t, \dot{y}_t)\) を予測するモデルを考える (\(t\) は時刻を表す)。

ただし、真の状態 \(\mathbf{x}_t\) は観測できないので、観測情報を用いて推定された値であることを明示するためにハット記号を用いて \(\hat{\mathbf{x}}_{t}\) のように書くことにしよう。

観測情報は通常何らかの計測誤差を含むので、観測情報 \(\mathbf{z}_t\) は真の状態に対してノイズを加算した形で \(\mathbf{z}_t = (x_t + \epsilon_x, y_t + \epsilon_y)\) のように表される。

状態から特定の要素を取り出すような行列 \(\mathbf{H}\) を用いると、次の 観測方程式 が得られる。

(7.9)\[\begin{split} \mathbf{z}_t = \mathbf{H} \mathbf{x}_t + \boldsymbol\epsilon_t, \qquad \mathbf{H} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{pmatrix} \end{split}\]

ただし、観測誤差 \(\boldsymbol\epsilon_t\) は平均が \(\mathbf{0}\) で共分散行列が \(\mathbf{R}\) であるような多次元ガウス分布に従うと仮定する。また、(7.9) においては、推定状態である \(\hat{\mathbf{x}}_t\) ではなく、真の状態 \(\mathbf{x}_t\) を用いていることに注意してほしい。

そして、観測方程式は見方を変えると、観測状態 \(\mathbf{z}_t\) が

(7.10)\[ \mathbf{z}_t \sim \mathcal{N}(\mathbf{H} \mathbf{x}_t, \mathbf{R}) \]

という形で多変量正規分布に従うことを表している。

状態方程式

次に状態の変化について考えてみよう。現在考えているモデルは状態を記述するために位置 \((x_t, y_t)\) と速度 \((\dot{x}_t, \dot{y}_t)\) を用いている。

従って、時刻 \(t - 1\) と時刻 \(t\) の間隔を \(\Delta t\) とすると、状態は次のように変化すると考えられる。

\[\begin{split} \begin{align*} x_{t} &= x_{t-1} + \dot{x}_{t-1} \Delta t \\ y_{t} &= y_{t-1} + \dot{y}_{t-1} \Delta t \end{align*} \end{split}\]

これをベクトル \(\mathbf{x}_t\) を用いて書くと、次のように表せる。

\[\begin{split} \mathbf{x}_{t} = \mathbf{F} \mathbf{x}_{t-1}, \qquad \mathbf{F} = \begin{pmatrix} 1 & 0 & \Delta t & 0 \\ 0 & 1 & 0 & \Delta t \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \end{split}\]

しかし、物体の状態を「実際に」記述している変数は位置と速度だけではないだろう。例えば、物体の加速度や回転に関する情報も必要かもしれない。

Kalmanフィルタでは、このような 考慮していない情報が状態に与える影響はノイズとして扱って予測を行う。ノイズの成分を \(\boldsymbol\eta_t\) と書くと、状態推定量 \(\hat{\mathbf{x}}_t\) の変化は次の 状態方程式 によって表せる。

(7.11)\[ \hat{\mathbf{x}}_{t}^{-} = \mathbf{F} \hat{\mathbf{x}}_{t-1} + \boldsymbol\eta_t \]

ただし、ノイズ成分 \(\boldsymbol\eta_t\) は平均が \(\mathbf{0}\) で共分散行列が \(\mathbf{Q}\) であるような多次元ガウス分布に従うと仮定する。

また、(7.11) において \(\hat{\mathbf{x}}_{t}^{-}\) は 観測情報を用いない仮の予測状態 であることを表すことに注意してほしい。Kalmanフィルタでは、この仮の予測を観測情報を用いて更新することで、次の時刻における状態推定量を求める。

---

ここで、状態推定値 \(\hat{\mathbf{x}}_t\) が従う確率密度分布も定義しておこう。

時刻0における状態推定値 \(\hat{\mathbf{x}}_0\) が平均 \(\mathbf{0}\) で共分散行列が \(\mathbf{P}_0\) の多変量正規分布に従う「不確定性」を持つと考える。

同様に、\(\hat{\mathbf{x}}_{t-1}\) が共分散行列を \(\mathbf{P}_{t-1}\) とする不確定性を持つとしよう。すると、(7.11) に従って状態が更新されたあとの \(\hat{\mathbf{x}}_t\) が持つ不確定性は行列 \(\mathbf{F}\) の効果と新たに加わるノイズ \(\boldsymbol\eta_t\) の影響を考慮して

(7.12)\[ \mathbf{P}_t^{-} = \mathbf{F} \mathbf{P}_{t-1} \mathbf{F}^T + \mathbf{Q} \]

を共分散行列とする不確定性を持つことが分かる。ここでは、不定性の更新に観測情報を用いていないので、左辺の \(\hat{\mathbf{x}}_t^{-}\) は観測情報を用いない仮の予測状態を表す。

(7.12) は、言い換えれば、状態推定値 \(\hat{\mathbf{x}}_t\) が平均を \(\mathbf{x}_t^{-}\), 共分散行列を \(\mathbf{P}_t^{-}\) とする多変量正規分布に従うことを意味する。

重要なことは、多変量正規分布の定義から、状態推定値 \(\hat{\mathbf{x}}_t\) と真の状態 \(\mathbf{x}_t^{-}\) の関係を逆に捉えることも可能だということで、真の状態 \(\mathbf{x}_t\) が、

(7.13)\[ \mathbf{x}_t \sim \mathcal{N}(\hat{\mathbf{x}}_t^{-}, \mathbf{P}_t^{-}) \]

という形で、平均を \(\hat{\mathbf{x}}_t\), 共分散行列を \(\mathbf{P}_t\) とする多変量正規分布に従うと考えることもできる。

状態の予測と更新

ここまでに示した (7.10) と (7.13) の2つの分布は、それぞれ \(\mathbf{x}_t\) が従う事前分布と \(\mathbf{z}_t\) の \(\mathbf{x}_t\) に対する事後分布と捉えることができる。

ここから、Bayesの定理を用いて、観測状態 \(\mathbf{z}_t\) が与えられたときの状態 \(\mathbf{x}_t\) の事後分布を求めよう。

まず、Bayesの定理から

\[ P(\mathbf{x}_t | \mathbf{z}_t) = \frac{P(\mathbf{z}_t | \mathbf{x}_t) P(\mathbf{x}_t)}{P(\mathbf{z}_t)} \]

であり、この部分は \(\mathbf{x}_t\) に依らないので定数とみなして良い。すると、 (7.10) と (7.13) から、

\[\begin{split} \begin{align*} P(\mathbf{x}_t | \mathbf{z}_t) &\propto P(\mathbf{z}_t | \mathbf{x}_t) P(\mathbf{x}_t) \\ &= \exp\left( -\frac{1}{2} \left[ \left( \mathbf{z}_t - \mathbf{H} \mathbf{x}_t \right)^\top \mathbf{R}^{-1} \left( \mathbf{z}_t - \mathbf{H} \mathbf{x}_t \right) + \left( \mathbf{x}_t - \hat{\mathbf{x}}_t^{-} \right)^\top \mathbf{P}_t^{-1} \left( \mathbf{x}_t - \hat{\mathbf{x}}_t^{-} \right) \right] \right) \\ \end{align*} \end{split}\]

と書けるので、指数部分の二次式を平方完成して整理すると、\(P(\mathbf{x}_t | \mathbf{z}_t)\) に対応する多変量正規分布の平均 \(\boldsymbol\mu\) と共分散行列 \(\boldsymbol\Sigma\) は次のように書ける。

\[\begin{split} \begin{align*} \boldsymbol\mu &= \hat{\mathbf{x}}_t + \mathbf{K}_t \left( \mathbf{z}_t - \mathbf{H} \hat{\mathbf{x}}_t \right) \\ \boldsymbol\Sigma &= \mathbf{P}_t^{-} - \mathbf{K}_t \mathbf{H} \mathbf{P}_t^{-} \end{align*} \end{split}\]

この式中の \(\mathbf{K}_t\) は Kalmanゲイン と呼ばれる行列で、次のように定義される。

\[ \mathbf{K} = \mathbf{P}_t^{-} \mathbf{H}^\top \left( \mathbf{H} \mathbf{P}_t^{-} \mathbf{H}^\top + \mathbf{R} \right)^{-1} \]

以上をまとめると、Kalmanフィルタによる状態の予測と更新は次のように表せる。

以下は、Mean-ShiftトラッキングとKalmanフィルタを組み合わせた物体追跡の結果である。

いかがだろうか。先ほどのMean-Shiftトラックングだけを用いた結果と比べると、関心領域の矩形の揺れが低減され、物体の移動に対してより頑健なトラッキングが実現できていることが分かるだろう。