2. 演習: 画像フィルタと幾何変換#
2.1. はじめに#
レポートは テンプレートファイル を使用して作成してください。また、ファイル名は 「(7桁の学籍番号)_第x回_画像処理レポート.docx」 (xの部分は何回目の課題なのかを記入)に変更してください。
課題作成上の注意
課題を作成する際には、プログラムは別に .py ファイルで作成して、本レポートと一緒に圧縮したうえで提出してください。また、Jupyter Notebook形式のファイル (拡張子が.ipynb)のものは受け付けません。
加えて、プログラムを添付したのみで内容に関する説明や結果に関する考察のないもの、単なる結果の羅列になっているもの(またはそのように見えるもの)は採点しませんのでご注意ください。
2.1.1. OpenCVによる線形フィルタ#
線形フィルタをOpenCVを用いて実装する際には、カーネル関数を何らかの離散的な二次元テーブルとして用意したうえで cv2.filter2D を用いる。以下に3×3のGaussianフィルタの実装例を示す。なお、以下のコードで cv2.filter2D の第2引数に与えている -1 は出力画像の型を表す変数で、入力画像を同じ型で出力する場合には -1 を指定すれば良い。
import cv2
import numpy as np
import skimage.data
import matplotlib.pyplot as plt
import japanize_matplotlib
japanize_matplotlib.japanize()
# 画像の読み込み
img = skimage.data.astronaut()
# フィルタカーネルの用意
K = np.array([[1, 2, 1], [2, 4, 2], [1, 2, 1]], dtype=np.float32) / 16.0
# フィルタの適用
res = cv2.filter2D(img, -1, K)
# 画像の表示
fig = plt.figure()
ax = fig.add_subplot(121)
ax.imshow(img)
ax.set_title("入力画像")
ax.axis("off")
ax = fig.add_subplot(122)
ax.imshow(res)
ax.set_title("フィルタ結果")
ax.axis("off")
plt.tight_layout()
plt.show()

2.1.2. NumPyによるFourier変換#
NumPyを用いて二次元Fourier変換を行うには np.fft.fft2 を用いれば良い。この関数は axes=... に指定された2つの軸に沿ってFourier変換を行う。画像の場合には、第0軸が画像の行、第1軸が画像の列に対応するので、axes=(0, 1) と指定すれば良い。
なお、逆Fourier変換は np.fft.ifft2 を用いる。以下に、NumPyを用いたFourier変換の実装例を示す。
import numpy as np
import skimage.data
img = skimage.data.astronaut() # 入力画像
img = (img / 255.0).astype(np.float32) # float32に変換
freq = np.fft.fft2(img, axes=(0, 1)) # 2次元FFT
なお、Fourier変換の結果は複素数であるため、そのままでは表示ができない。そこで、各周波数成分の大きさをノルムとして求めて、その強度を表示してみる。このような各周波数における信号強度をパワースペクトルと呼ぶ。
パワースペクトルを画像として表示する際には、その対数をとって表示することが多い。パワースペクトルの表示例を以下に示す。
import matplotlib.pyplot as plt
import japanize_matplotlib
japanize_matplotlib.japanize()
# パワースペクトルの計算 (振幅の二乗)
ps = np.sum(np.abs(freq) ** 2, axis=2)
# パワースペクトル画像の描画
fig, ax = plt.subplots()
ax.imshow(np.log(ps + 1.0e-12), cmap="gray") # 対数を取って表示
ax.set_title("パワースペクトル画像 (コーナーが原点)")
plt.show()
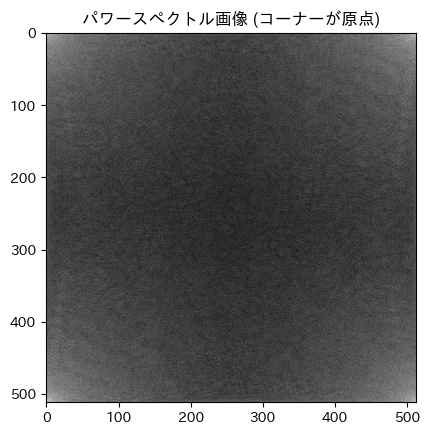
この図から分かるように、np.fft.fft2 の結果は画像のコーナーが原点になるような座標系を使っている。この座標系を画像の中心が原点になるような座標系に直すには np.fft.fftshift を用いる。
# 原点を中心にする
freq = np.fft.fftshift(freq, axes=(0, 1))
# パワースペクトルの計算 (振幅の二乗)
ps = np.sum(np.abs(freq) ** 2, axis=2)
# パワースペクトル画像の描画
fig, ax = plt.subplots()
ax.imshow(np.log(ps + 1.0e-12), cmap="gray") # 対数を取って表示
ax.set_title("パワースペクトル画像 (中心が原点)")
plt.show()
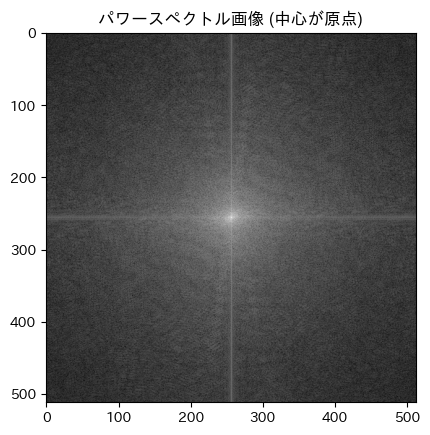
ここから逆Fourier変換で元の画像を復元する際には、まず np.fft.ifftshift を用いて画像のコーナーが原点の座標系に戻してから、np.fft.ifft2 を用いて信号を画像空間に戻す。以下にその実装例を示す。
freq = np.fft.ifftshift(freq, axes=(0, 1)) # 原点を画像のコーナーに戻す
repro = np.fft.ifft2(freq, axes=(0, 1)) # 逆FFT
repro = np.real(repro) # 実部だけを取り出す (虚部はほとんどゼロ)
repro = np.clip(repro, 0.0, 1.0) # 0-1にクリッピング
# 元画像と復元画像の表示
fig = plt.figure()
ax = fig.add_subplot(121)
ax.imshow(img, vmin=0.0, vmax=1.0)
ax.set_title("元画像")
ax.axis("off")
ax = fig.add_subplot(122)
ax.imshow(repro, vmin=0.0, vmax=1.0)
ax.set_title("Fourier変換・逆変換で復元")
ax.axis("off")
plt.tight_layout()
plt.show()

2.1.3. 周波数空間でのフィルタ処理#
GaussianフィルタやSobelフィルタなど、画像空間でカーネル関数が定義されるフィルタを周波数空間で適用する場合、画像とカーネル関数の両方をFourier変換してから、周波数空間で要素積を取り、その後で逆Fourier変換を行えば良いと述べた。
しかし、Fourier変換の結果得られる周波数空間の画像サイズは元の画像サイズと同じであるため、周波数空間でカーネル関数のFourier変換と要素積を取るためには、カーネル関数を元の画像と同じ座標系の上で事前計算しておく必要がある。
このようなカーネル関数の事前計算においては、画像の中心が原点となるような座標系を用い、その結果をコーナーが原点になるような座標系に修正してから、Fourier変換で周波数領域に変換する。
この方法の実装例を以下に示す。
import numpy as np
import skimage.data
img = skimage.data.astronaut() # 入力画像
img = (img / 255.0).astype(np.float32) # 0-1の範囲の実数に変換
H, W, _ = img.shape
# (H, W) の二次元グリッドを作成
ys, xs = np.mgrid[0:H, 0:W]
# 原点が中心に成るようにシフト
ys = ys - H // 2
xs = xs - W // 2
# Gaussianカーネルの計算
sigma = 2.0
kern = np.exp(-(xs**2 + ys**2) / (2 * sigma**2))
kern = kern / np.sum(kern) # 正規化
# Fourier変換
K = np.fft.ifftshift(kern, axes=(0, 1)) # 原点を画像のコーナーに移動
K = np.fft.fft2(K, axes=(0, 1)) # FFT
# 画像もFourier変換
freq = np.fft.fft2(img, axes=(0, 1)) # FFT
# 周波数空間で要素積を取る
freq = freq * K[..., None]
# 逆FFT
res = np.fft.ifft2(freq, axes=(0, 1)) # 逆FFT
res = np.real(res) # 実部だけを取り出す
res = np.clip(res, 0.0, 1.0) # 0-1にクリッピング
# 元画像とフィルタ結果の表示
fig = plt.figure()
ax = fig.add_subplot(121)
ax.imshow(img, vmin=0.0, vmax=1.0)
ax.set_title("元画像")
ax.axis("off")
ax = fig.add_subplot(122)
ax.imshow(res, vmin=0.0, vmax=1.0)
ax.set_title("Gaussianフィルタ結果")
ax.axis("off")
plt.tight_layout()
plt.show()

以上のように、周波数領域でフィルタ処理を行う場合には画像のFourier変換と、カーネル関数のFourier変換の結果において、どこを原点とした座標系を用いているかに留意する必要があるので注意してほしい。
2.2. 演習問題#
Sobelフィルタの実装
cv2.filter2D を用いて3×3のSobelフィルタを適用するプログラムを作成し、x方向とy方向のエッジを検出せよ。
Fourier変換の計算量
NumPyに実装されている二次元Fourier変換 np.fft.fft2 を \(N \times N\) の画像に適用した場合に、画像サイズ \(N\) に対して計算量がどのように増えていくかを実際にプログラムを書いて確かめよ。Fourier変換する画像は np.random.rand(N, N) で生成したランダムな画像を用いれば良い。
周波数領域でのGaussianフィルタ
Gaussianフィルタのカーネル関数は平滑化の強度を調整するパラメータとして \(\sigma\) を持つ。このカーネル関数のFourier変換を求め、周波数領域での \(\sigma\) の意味を考察せよ。
ホモグラフィ変換による画像の正規化
OpenCVの関数 cv2.getPerspectiveTransform を用いると、変換前後の4点を指定することで射影変換を表す4×4の行列を得ることができる。また、その射影変換行列を用いてホモグラフィ変換を行うには cv2.warpPerspective を用いる。次の画像に対してホモグラフィ変換を施すことで、画像に映り込んだ数独の問題が画像全体に映るように正規化せよ。
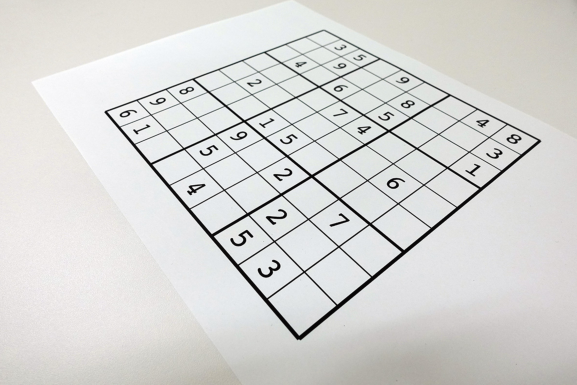
なお、変換前の画像において、数独の問題の角の4点は以下の座標を持つものとし、正規化後は画像サイズが256×256になるように変換すること。
左上: (x, y) = (324, 30)
右上: (x, y) = (540, 141)
右下: (x, y) = (298, 339)
左下: (x, y) = (105, 111)
2.3. 補足: Pythonでの画像フィルタの実装#
Pythonで2次元のフィルタを実装する場合、素直にfor文を二重にしてしまうと、計算に時間がかかりすぎてしまう。これを避けるには、C++で実装すれば良い NumPyの機能を上手く使って実装する必要がある。
特に非線形フィルタを実装する場合には、単なる畳み込み演算にはならず、OpenCVに実装されている二次元畳み込みの関数 (cv2.filter2D) が利用できないので、何らかの工夫が必要になる。
2.3.1. カーネルとの重み付き和の計算をNumPyで行う#
カーネル関数との畳み込みは各画素に対する二重ループ (x, yの各座標に対して1次元のループ)が必要で、さらに二次元のカーネル関数との画素の重み付き和の計算に二重ループが必要になる。しがって、全体としては四重のループが必要になり、for文の繰り返し計算に特に時間を要するPythonでは、比較的小さな画像であっても、かなりの時間を要する。
そこで、まず考えられる工夫はバイラテラル・フィルタのフィルタカーネルをNumPyの二次元配列に対する操作によって効率的に計算する、という方法である。
バイラテラル・フィルタのカーネル関数は色の差に関するGauss関数と空間的な距離に関するGauss関数の積であったので、次のような形で画像の一部を切り出すことでNumPyの配列操作により求めることが可能である。
# フィルタ範囲の取り出し
region = img_pad[y : y + ksize, x : x + ksize, :]
center = img_pad[y + pad, x + pad, :]
# 色カーネルの計算
d = region - center
d2 = np.sum(d * d, axis=-1)
L = np.exp(-0.5 * d2 / (sigma_r * sigma_r))
# カーネルの合成
W = K * L
W /= np.sum(W)
# 出力画素値の計算
res[y, x] = np.sum(region * W[..., None], axis=(0, 1))
少々、長文のコードになるが、以下に、この考え方を用いたバイラテラル・フィルタの実装例を示す。
import time
import numpy as np
import skimage.data
import matplotlib.pyplot as plt
import japanize_matplotlib
# 画像の用意 (単精度浮動小数に変換しておく)
img = skimage.data.chelsea()
img = (img / 255.0).astype(np.float32)
height, width, _ = img.shape
# 時間計測開始
start_time = time.perf_counter()
# フィルタのパラメータ
ksize = 9
sigma_s = 5.0
sigma_r = 0.1
# 位置カーネルの事前計算
kx = np.arange(ksize) - ksize // 2
ky = np.arange(ksize) - ksize // 2
ky, kx = np.meshgrid(ky, kx, indexing="ij")
K = np.exp(-0.5 * (kx * kx + ky * ky) / (sigma_s * sigma_s))
# 画像をあらかじめパディング
pad = ksize // 2
img_pad = np.pad(img, ((pad, pad), (pad, pad), (0, 0)), mode="edge")
# フィルタ処理
res = np.zeros_like(img)
for y in range(height):
for x in range(width):
# フィルタ範囲の取り出し
region = img_pad[y : y + ksize, x : x + ksize, :]
center = img_pad[y + pad, x + pad, :]
# 色カーネルの計算
d = region - center
d2 = np.sum(d * d, axis=-1)
L = np.exp(-0.5 * d2 / (sigma_r * sigma_r))
# カーネルの合成
W = K * L
W /= np.sum(W)
# 出力画素値の計算
res[y, x] = np.sum(region * W[..., None], axis=(0, 1))
# 時間計測終了
end_time = time.perf_counter()
elapsed_time = end_time - start_time
# 画像の表示
fig = plt.figure()
gs = fig.add_gridspec(1, 2)
ax = plt.subplot(gs[0])
ax.imshow(img)
ax.set_title("元画像")
ax.set(xticks=[], yticks=[])
ax = plt.subplot(gs[1])
ax.imshow(res)
ax.set_title(f"バイラテラル・フィルタ ({elapsed_time:.2f}秒)")
ax.set(xticks=[], yticks=[])
fig.tight_layout()
plt.show()

2.3.2. スライドウィンドウ分割の利用#
上記の方法でも、四重ループのfor文を用いるよりはかなり計算が早くなるが、それでも450×300の画像に対して1秒程度要しており、決して高速とは言えない。
ここまでのコードでは画像の各画素の周囲の領域を取り出すためにNumPyのスライス (img_pad[y:y+ksize, x:x+ksize]のような書き方) を用いたが、この画像の一部の切り出しもfor文を用いる代わりにNumPyの関数 (C,C++等の言語で実装されており早い) を用いれば、より高速に計算できる可能性がある。
実際、NumPyには、numpy.lib.stride_tricks というモジュール内に slinding_window_view という関数が用意されていて、\((H, W, 3)\) という形の画像 img_pad に対して、 sliding_window_view(img_pad, (ksize, ksize, 3)) のように呼び出すと、画像が (H, W, ksize, ksize, 3) という形の5次元の配列に変換される。
この結果を用いれば、前述のカーネル関数の計算をすべての画素に対してNumPyの配列処理によって計算できるようになるので、さらなる高層化が期待できる。
再び、長文のコードになるが、以下に sliding_window_view を用いたバイラテラル・フィルタの実装例を示す。
import time
import numpy as np
import skimage.data
import matplotlib.pyplot as plt
import japanize_matplotlib
from numpy.lib.stride_tricks import sliding_window_view
# 画像の用意 (単精度浮動小数に変換しておく)
img = skimage.data.chelsea()
img = (img / 255.0).astype(np.float32)
height, width, _ = img.shape
# 時間計測開始
start_time = time.perf_counter()
# フィルタのパラメータ
ksize = 9
sigma_s = 5.0
sigma_r = 0.1
# 位置カーネルの事前計算
kx = np.arange(ksize) - ksize // 2
ky = np.arange(ksize) - ksize // 2
ky, kx = np.meshgrid(ky, kx, indexing="ij")
K = np.exp(-0.5 * (kx * kx + ky * ky) / (sigma_s * sigma_s))
# 画像をあらかじめパディング
pad = ksize // 2
img_pad = np.pad(img, ((pad, pad), (pad, pad), (0, 0)), mode="edge")
# 画素ごとのフィルタに必要な画像範囲をパッチとして取り出す
img_view = sliding_window_view(img_pad, (ksize, ksize, 3))
img_view = img_view.reshape(img.shape[0], img.shape[1], ksize, ksize, 3)
center = img_view[:, :, pad : pad + 1, pad : pad + 1, :]
# 色カーネルの計算
diff = img_view - center
d2 = np.sum(diff * diff, axis=-1)
L = np.exp(-0.5 * d2 / (sigma_r * sigma_r))
# カーネルの合成
W = K * L
W = W / np.sum(W, axis=(-1, -2), keepdims=True)
W = W.reshape(img.shape[0], img.shape[1], ksize, ksize, 1)
# 各パッチを一気に畳み込む
res = np.sum(img_view * W, axis=(-2, -3))
# 時間計測終了
end_time = time.perf_counter()
elapsed_time = end_time - start_time
# 画像の表示
fig = plt.figure()
gs = fig.add_gridspec(1, 2)
ax = plt.subplot(gs[0])
ax.imshow(img)
ax.set_title("元画像")
ax.set(xticks=[], yticks=[])
ax = plt.subplot(gs[1])
ax.imshow(res)
ax.set_title(f"バイラテラル・フィルタ ({elapsed_time:.2f}秒)")
ax.set(xticks=[], yticks=[])
fig.tight_layout()
plt.show()

こちらの実装は、この前に示した実装と比べて2-3倍程度早くなっており、450×300の画像に対して0.5秒と、まだまだ満足行く測度ではないもののPythonに閉じた実装としては、かなり高速に計算できるようになっている。
なお、実際にバイラテラル・フィルタが使えれば良いだけであれば、OpenCVに実装されている cv2.bilateralFilter を用いるのが高速かつ簡単だろう。
