1. デジタル画像の表現#
現在、写真といえばデジタル画像のことであり、多くは画素の色情報がデジタル、つまり二進数によって表される数字として記録している。しかし、従来、写真とは現実世界の光の強さの情報をデジタルデータやフィルム上に記録したものである。
本節では、写真とカメラの簡単な歴史を紹介した後に、代表的なデジタル画像の表現方法であるラスタ形式とベクタ形式について紹介する。
参考資料
『ディジタル画像処理 改訂第二版』 P.15 第2章 ディジタル画像の撮影
1.1. 写真とカメラの略史#
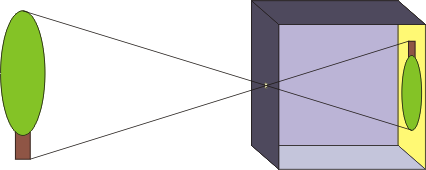
写真はカメラを用いることで撮影できるが、この「カメラ」という言葉の語源はラテン語で「暗い部屋」を意味する「カメラ・オブスクラ」である。カメラ・オブスクラは、箱に小さな穴 (ピンホール)を空けることで、箱の外の様子を箱の中に設置された板に投影する機材であった。
1.1.1. フィルムカメラ#
現在の写真のように、現実世界を写しとって保存できるようになったのは19世紀になってからのことで、初めて写真を撮ることに成功したのは、Joseph Nicéphore Niépceとされる。彼の写真は、光を当てると硬化する性質のある一種のアスファルト (bitumen of Judea)を使っており、それを塗布した樹脂板にピンホールから光を当てて、硬化していない部分を取り除くことで写真を得るというものであった。
昔のフィルムカメラのように「銀塩」(= ハロゲン化銀)を使って写真の撮影を試みたのは、Henry Talbotであり、彼のカメラは現在流通しているフィルムカメラのように、いわゆる「ネガ画像」を現像によって取得できた。そのためTalbotの方式は、Niépceの写真と違い、何枚も同じ写真を焼き増しすることができた。
20世紀のはじめになると商用のフィルムカメラがコダック社により発売された。この頃になると、フィルムがセルロイドで作られるようになり、それまでの紙のフィルムよりも写真の品質が安定するようになった。
銀塩を感光剤として用いる写真は、フィルムに銀塩、すなわちハロゲン化銀を塗布したものを用いる。銀塩に光が当たると、ハロゲン化銀の一部が銀結晶に変化する。
この銀結晶は微量であるため目視では確認はできないが、これを現像液に浸すと、銀結晶の周囲のハロゲン化銀だけが銀に変化し、光があたった部分が暗くなる。これにより、いわゆる「ネガ画像」が写ったフィルムである「ネガ」が得られる。
このネガを通した光を印画紙に当てて、再び現像と同様の工程を経ると、ネガのネガとして元の画像である「ポジ」が得られる、というのが銀塩を用いた写真の基本的な仕組みである。
1.1.2. デジタルカメラ#
デジタルカメラ の基盤技術であるCCD (Charged-Coupled Device)は、金属酸化膜半導体 (MOS, metal-oxide semiconductor)を用いて1970年に開発された [1]。開発に携わったWillard BoyleとGeorge E. Smithは2009年にノーベル物理学賞を受賞している。
CCDを用いた二次元イメージセンサにはいくつかの構造があるが、その一つであるインターライン方式のCCDイメージセンサ(図 1.2)は、各列 (あるいは各行)ごとにCCDが直列に繋がっており、各画素に光があたって電荷が生じると、その電荷をバケツリレーのように隣の画素に渡していく。各列の末端にあるCCDは横方向 (あるいは縦方向)に隣の列と繋がっており、各列の電荷は隣の列へと渡される。
最後に、集められた電荷がアナログ-デジタル変換されて離散的な画素値の情報として記録される。

CCDをイメージセンサに用いたデジタルカメラは1975年にコダック社で開発された。製造されたデジタルカメラは100×100画素の解像度を持つカメラであった。
一般向けに「開発」されたデジタルカメラは富士写真フイルム (現在の富士フイルム)が1988年に発表したFUJIX DS-1Pであった。ただし、実際には一般向けに販売されることはなく、実際には1989年にFUJIX DS-Xが一般向けに「販売」された。
ただし、FUJIX DS-Xは非常に高価であったため、一般向けに広く受け入れられたデジタルカメラとしてはDycam Model 1が広く知られている。
なお、現在、多くのデジタルカメラのイメージセンサにはCCDではなく CMOS (相補型金属酸化膜半導体)が広く用いられている。
CMOSは1画素のCCDが二次元に並べられたような構造となっており、1画素ごとに光電効果により生じる電荷を読み出すことができる。当初、CMOSは画素ごとの個体差により生じるノイズが問題視されていたが、CMOSはCCDに比べて安価に作成でき、読み出し速度が早いという優位性があり、徐々に性能改善が進んだことで、今日のデジタルカメラの標準となった。
CMOSイメージセンサがデジタルカメラに初めて搭載されたのは1996年に発売された東芝のアレグレット PDR-2であるとされている。
なお、現在、市販のデジタルカメラのほとんどがCMOSイメージセンサを採用しているが、産業用カメラやレントゲン写真器のような画質や感度が重要となる用途では、CCDイメージセンサが用いられることも多い。
写真とカメラの歴史
今日の「カメラ」という名前は「カメラ・オブスクラ」という室外の様子を室内に投影する仕組みに由来する。
CCDイメージセンサは初期のデジタルカメラに広く用いられていた。現在でも産業用や医療用の一部の応用では広く用いられている。
CMOSイメージセンサは、安価に作成でき、CCDよりも読み出しの速度が速い。当初、画質に課題を抱えていたが、現在は性能改善によりイメージセンサの主流となっている。
1.2. ラスタ画像#
ここまでは、写真をデジタルに撮影するための技術について紹介してきたが、いわゆるパーソナルコンピュータが普及するに従って、デジタルデータとしての写真を編集したり、コンピュータの中でイラストなどの画像を作成するという需要が生じてきた。
現在、デジタル画像の表現には大きく分けて、ラスタ形式 (raster format)とベクタ形式 (vector format)がある。
写真など、特に意図せずデジタル画像という言葉が使われているときには、ラスタ形式の画像を指すことが多い。ラスタ形式は、画素を格子状に並べ、各画素に色を割り振ることで画像が表現される。
注意
ラスタ形式で表現されたデジタル画像ををビットマップ画像と呼ぶこともあるが、画像のファイル形式の.bmpとは微妙に異なるので注意。
例えば、次の猫の画像は、縦300画素、横450画素の13万5000画素で表現されている。

また、各画素には色情報として (104, 120, 143) のような3つ組の値が記録されている。この三つの値は通常0から255の間の整数、すなわち 8ビット符号なし整数 によって表されることが多い。
色の表現については次節「 カラー画像と色空間 」で詳しく述べるが、世の中で広く用いられているJPEGやPNGなどの画像形式では、三つの整数は、赤、緑、青の三成分に対応している。
1.2.1. 画素による標本化#
現在、画素の集合で表されるデジタル画像は深く日常生活に浸透しているため、ここまでの説明において、「画像 = 画素の集まり」という説明に違和感を覚える読者は少ないのではないかと思う。
しかし、よく考えてみると、我々の生活している世界は 画素のような離散化された世界ではない 。ここで「画素」と読んでいるものは小さな矩形領域で、その内部が特定の色で塗りつぶされている。しかし、画素がどんなに小さな領域を覆う矩形であったとしても、現実世界では、その矩形領域内部は「一色」だけでは表現できない。
今日、市販のスマートフォンやデジタルカメラで撮影できる画像は縦横に数千の画素が並んでいるが、もし画像の解像度が低く数百あるいは数十程度しか画素がなければ、この事実は容易に理解できるだろう。

以上を踏まえると、ラスタ画像は 現実世界にある連続的な信号を格子状に並んだ点でサンプリングしたもの であると見なせる。このように連続的な対象を離散的な点の集合によって表現することを 標本化 (sampling) と呼ぶ。
1.2.2. 色情報の量子化#
現実世界の色、というのは 波長の異なる光が人間の脳内で処理された結果 であると考えることができる。人間の持つ視細胞は主に赤、緑、青に対応する波長に強く反応するため、多くのデジタル画像表現では、色の表現に赤、緑、青の3成分を表す数値の組を用いる。
では、人間の脳で、赤色に対応する波長の光が処理される時に、その反応の強さは0-255のような離散的な値なのか、といえば、当然ながらそうではない。
従って、デジタル画像において、赤、緑、青の各成分が0-255の8ビット符号なし整数で表されているというのは、あくまで形式的なものに過ぎず、色に対応する光の強さは、「光の強さレベル」で離散化されている。
このように、アナログ信号として得られる光強度の実数値を、解像度が有限なデジタル値に置き換える処理を 量子化 と呼ぶ。
色を表す光の強度は物理的には放射照度 \(E\) (単位: \(\mathrm{[W/m^2]}\))に対応しており、この強度は正の実数全体で値を取りうる。
ただし、現実的には、光の強度は特定の範囲に \(E_{\text{min}}\) から \(E_{\text{max}}\) に収まっていると考えられるため、
のように、値が0から1の範囲に収まるように正規化する。量子化に用いるビット数を \(B\) とすると、この \(E'\) に \(2^B\) を乗じて整数に直すことで、最終的な画素値が得られる。
この際、とある画素に101のような値が保存されているとして、これが101から102の間の実数値でどれに対応するのかを知ることはできず、0から1の範囲で考えたときに、最大 \(2^{-B}\) の誤差が生じる。この誤差を 量子化誤差 と呼ぶ。より多くのビットを用いると量子化誤差は小さくなるため、元の信号をより忠実に表せるようになる。
通常、1画素あたりのデータ量は赤、緑、青の各成分に8ビットずつの合計24ビットである。1画素を表すのに用いられるビット数のことを特にビット深度と呼び、一般的なカラー画像は24ビット深度を持つ。
PNG形式などの一部のラスタ画像形式はさらに8ビットで画素の透明度を表すような32ビット深度の形式も表せる他、デジタル一眼レフのような高価なカメラではRAW画像と呼ばれるビット深度の大きな画像を得ることもできる。
ラスタ画像
ラスタ画像は画素の集合で表現されるデジタル画像であり、カラー画像の場合、通常、各画素には赤、緑、青の三成分を表す整数が記録されている。
「画素」は連続的な実世界を離散的な点の集合でサンプリングしたものであり、このような離散点による表現への変換を標本化と呼ぶ。
画素に記録された色情報はアナログな光強度をデジタル値である整数値で表現し直したもので、この操作を量子化と呼ぶ。
1.2.3. ラスタ画像の圧縮#
ここまで、多くのラスタ画像形式は赤、緑、青の3色を各8ビットで表現していることを述べた。従って、1画素あたりのデータ量は24ビット、すなわち3バイトである。これを300×450画素の画像に当てはめると、405000バイト、すなわち約405キロバイトのデータ量が必要となる。
では、前述の猫の画像を実際に各自のコンピュータにダウンロードして、そのデータサイズを確認してみてほしい。一体、どのくらいのデータ量になっているだろうか?
画像をダウンロードすると、ファイルはPNG (portable network graphics)形式で保存されている。おそらく画像のサイズは223キロバイト程度になっているはずで、これは実際に画像を表すのに必要な405キロバイトよりもかなり小さくなっている。
また、画像を別のファイル形式であるJPEG (Joint Photographic Experts Group)形式で保存すると、さらに画像が小さくなるはずだ。ウェブ上にはPNG形式の画像をJPEG形式の画像に変換するためのツールがあるので、それらを使ってファイルサイズを確かめてみよう。
練習問題
検索エンジンで「PNG to JPEG converter」などと検索して表示されるウェブサイトを使って、PNG形式の画像をJPEG形式の画像に変換せよ。その際、変換後の画像のデータサイズが何キロバイトになるかを確かめよ。
JPEG形式の画像がどの程度のデータサイズになるかは、圧縮の度合いによって異なるが、概ね数十キロバイト程度までデータサイズを圧縮できているのではないだろうか。
画像のデータは一般にサイズが大きく、多数の画像を限られたストレージに保存するには、データ圧縮されることが望ましい。画像の圧縮方式には 不可逆圧縮 (lossy compression) と 可逆圧縮 (lossless compression) の2種類がある。
例えば、前述のJPEG形式は不可逆圧縮であり、一度圧縮してしまうと、圧縮前の元画像を復元することはできない。一方、PNG形式は可逆圧縮であり、データサイズを削減しながら、元の画像を完全に復元することができる。一般に、可逆圧縮よりも不可逆圧縮の方が高い圧縮率を得ることができ、写真のような自然画像を圧縮する場合には、その品質を損なうことも少ない。
JPEG形式#
JPEG形式の画像圧縮には、離散コサイン変換が用いられる。離散コサイン変換は、特定の信号を余弦関数の重ね合わせによって表現する手法であり、画像にどの程度の周波数の信号が含まれているかを調べることができる。
人間の視覚は、特定の周波数の成分が大きくなったり小さくなったりしたとしても、画像の変化に気づきづらいという特性がある。そこで、JPEG形式の画像圧縮では、画像を8×8のブロックに分割した後、各ブロックごとに離散コサイン変換を行って、画像を周波数成分の情報に変換する。
その後、周波数成分の情報をハフマン符号とランレングス符号化によって更に圧縮する。この際、特定の周波数成分の情報が量子化によって部分的に失われるため、JPEG形式は不可逆圧縮である。
実際、JPEG形式で画像を圧縮すると、圧縮率に応じて、 ブロックノイズ や モスキートノイズ と呼ばれる画像の劣化 (専門的にはアーティファクト (artifact)と呼ぶ)が生じる。
詳細なJPEG圧縮のアルゴリズムについて本項で述べることはしないが、興味のある読者は拙書の講義資料 JPEG圧縮の概要 や [2] を参照されたい。
PNG形式#
PNG形式の画像圧縮にはLZ77符号化と呼ばれるアルゴリズムとハフマン符号を組み合わせた Deflate と呼ばれる手法が用いられている。Deflateは一般的なファイル圧縮方法であるZIP形式にも用いられている。ZIP形式は圧縮されたデータを損なってしまってはいけないため、Deflateが可逆圧縮であることは容易に想像できる。
Deflateで用いられるLZ77符号化には、スライド辞書と呼ばれる動的な辞書が用いられる。このスライド辞書は先頭から順にデータを見ていく際に、一定範囲の直近の内容を辞書として用いる。データを走査中に、辞書内に含まれるデータ列が見つかった場合には、辞書上の位置と一致するデータ長を記録することでデータを圧縮する。
PNG形式の画像圧縮は画素を縦方向、あるいは横方向の走査線ごとに圧縮する。ただし、走査線上に並ぶ画素値は必ずしもLZ77符号化で上手く圧縮できるような繰り返しを含むものばかりではないので、各走査線に対して、隣接する画素との平均や差分を取るなどの前処理 (フィルタリング)を施し、より高い圧縮率が得られるように工夫している。
練習問題
画像圧縮には、文中で紹介したJPEG形式やPNG形式の他にも、GIF形式やWebP形式などの多数の圧縮アルゴリズムが用いられる。これらの圧縮アルゴルズムを以下の観点で比較し、各アルゴリズムがどのような応用に適しているかを考察せよ。
可逆圧縮か不可逆圧縮か
圧縮率
圧縮と展開の速度
透明度の扱い
扱えるビット深度
1.3. ベクタ画像#
ベクタ画像は、イラストのような線や特定の色で塗りつぶされた図形の組み合わせで画像を表現する。この際、図形は数式のような形で表現されているため、画像を拡大・縮小したとしても、その拡大率に応じた画像を数式から計算し直すことで、常にボケのない鮮明な画像を得ることができる。ここで「数式」と読んでいるものは、2点を通る直線の式や、とある点を中心とする円の他、曲線を表す多項式などが含まれる。
ベクタ画像を実際の通常のディスプレイ (より厳密にはラスタスキャン型のディスプレイ)に描画するためには、この数式を画素によって標本化されたラスタ画像に変換する必要がある。このように数式で表された図形をラスタ画像のような視覚情報に変換する処理を レンダリング と呼ぶ。
1.3.1. 直線の描画#
とある平面に \((x_0, y_0)\) と \((x_1, y_1)\) を結ぶ線分を描く場合を考えてみよう。もっとも単純には、 \(x_0\)から\(x_1\)までの整数に対して、その点に対応するy座標を計算し、そのy座標を四捨五入等により整数に直して得られる格子点を黒く塗りつぶせば良い。
これをPythonのプログラムとして実装し、\((50, 100)\)と\((200, 150)\)を結ぶ線分を描画するとすると、ソースコードは次のようになる。
import numpy as np
import matplotlib.pyplot as plt
SIZE = 256 # 画像のサイズ
BG_COLOR = np.array([255, 255, 255], dtype=np.uint8) # 背景の色
FG_COLOR = np.array([0, 0, 255], dtype=np.uint8) # 線の色
x0, y0 = 50, 100 # 始点の座標
x1, y1 = 200, 150 # 終点の座標
decline = (y1 - y0) / (x1 - x0) # 直線の傾き
# 背景が白の画像を作成
image = np.full((SIZE, SIZE, 3), BG_COLOR, dtype=np.uint8)
# 直線を描画
for x in range(x0, x1 + 1):
y = y0 + (x - x0) * decline
y = int(y + 0.5) # 四捨五入
image[y, x] = FG_COLOR
# 画像を表示
# NOTE: interpolation=Noneを指定して、実際の画像をそのまま表示
fig, ax = plt.subplots()
ax.imshow(image, vmin=0, vmax=255, interpolation=None)
ax.grid(False)
plt.show()
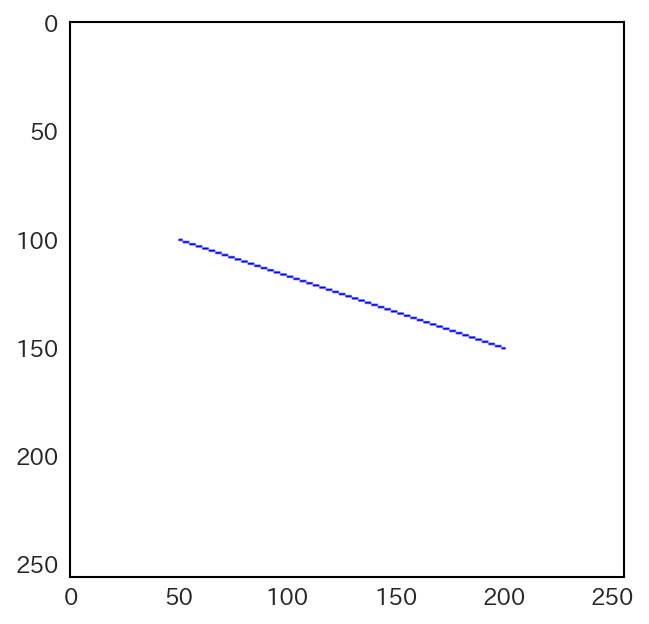
しかし、この方法では、\(| x_1 - x_0| > |y_1 - y_0|\) の場合であれば上手く線分を描画できるが、その反対に \(| x_1 - x_0| < |y_1 - y_0|\) の場合には、線分が途切れ途切れに描画されてしまう。
実際、先ほどの始点と終点の座標においてx座標とy座標を入れ替え、\((100, 50)\)と\((150, 200)\)を結ぶ線分を描画すると、次のような結果になる。
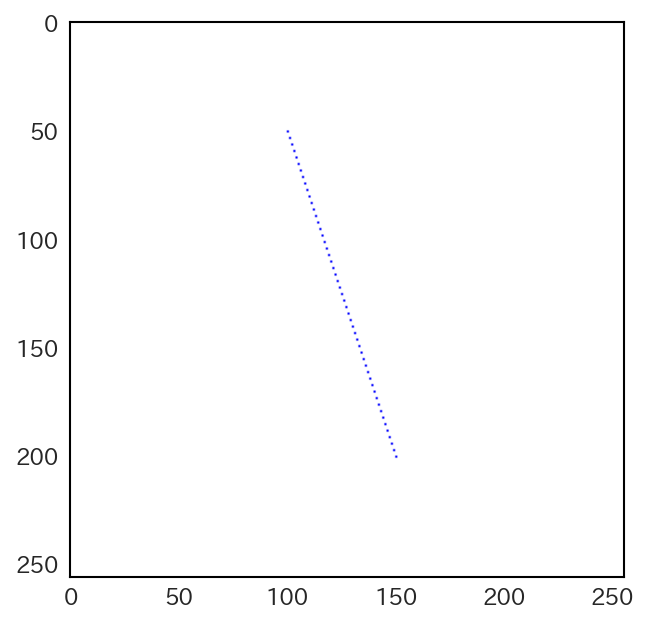
この問題を解決するには、 \(| x_1 - x_0 |\) と \(| y_1 - y_0 |\) を比較して、大きな値を取る方の座標を1ずつ大きくするように工夫すれば良い。
プログラムの効率的な書き方はいろいろと考えられるが、以下のソースコードでは、描画する点の数を nとし、描画する点のx座標とy座標が、それぞれdxとdyだけ増加すると考え、 \(| x_1 - x_0 |\) と \(| y_1 - y_0 |\) の大小に応じて n, dx, dyの値を設定している。
import numpy as np
import matplotlib.pyplot as plt
SIZE = 256 # 画像のサイズ
BG_COLOR = np.array([255, 255, 255], dtype=np.uint8) # 背景の色
FG_COLOR = np.array([0, 0, 255], dtype=np.uint8) # 線の色
x0, y0 = 100, 50 # 始点の座標
x1, y1 = 150, 200 # 終点の座標
# x, yの大小によって場合分け
# n: 描画する点の数
# dx, dy: 1ステップでのx, yの変化量
if abs(x1 - x0) < abs(y1 - y0):
if y0 > y1:
x0, y0 = y0, x0
x1, y1 = y1, x1
n = abs(y1 - y0)
dx = (x1 - x0) / (y1 - y0)
dy = 1.0
else:
if x0 > x1:
x0, y0 = x1, y1
x1, y1 = x0, y0
n = abs(x1 - x0)
dx = 1.0
dy = (y1 - y0) / (x1 - x0)
# 背景が白の画像を作成
image = np.full((256, 256, 3), BG_COLOR, dtype=np.uint8)
# 直線を描画
for i in range(n + 1):
x = int(x0 + i * dx + 0.5)
y = int(y0 + i * dy + 0.5)
image[y, x] = FG_COLOR
# 画像を表示
fig, ax = plt.subplots()
ax.imshow(image, vmin=0, vmax=255, interpolation=None)
ax.grid(False)
plt.show()
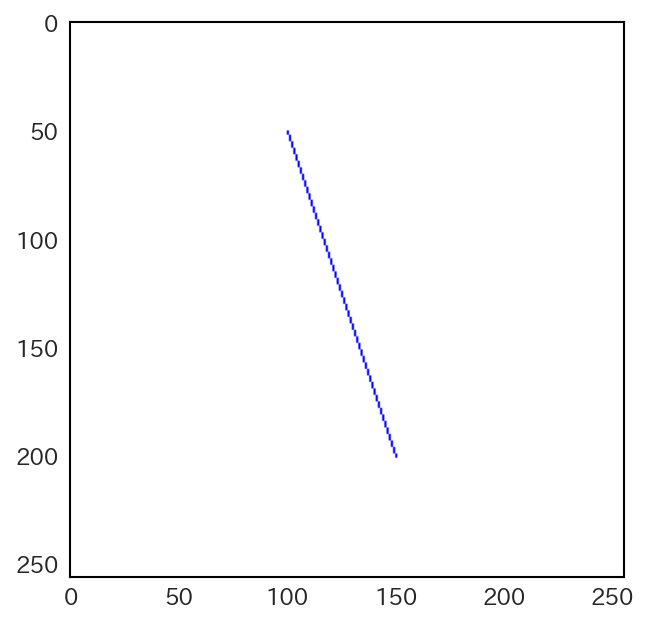
図 1.3 直線の描画結果#
1.3.2. アンチエイリアシング#
前述の図 1.3では、線分が完全に黒の画素 (画素値が0)の集合として描画されている。しかし、このような描画方法では、線分がギザギザしたような見た目になってしまうという問題が起こる。このようなギザギザの見た目をジャギーと呼ぶ。
ジャギーは専門用語では エイリアシング の一種であり、線分の傾きの大きさに対して画素のサンプルが不十分である場合に起こる (簡単には、画像の解像度を上げれば解決する)。エイリアシングを防ぐ描画技術のことを一般に アンチエイリアシング と呼ぶ。アンチエイリアシングは、描画対象の空間解像度をフィルタ処理によって低下させることで、標本化によるエイリアシングの発生を抑制する。
直線の描画にアンチエイリアシングを施す最も単純な手法は、実数値の座標と描画先の格子点とのずれの量に応じて、描画する色の濃さを調整することである。以下では、その代表的なアルゴリズムとして Xiaolin Wuのアルゴリズム [3] を紹介する。
Xiaolin Wuのアルゴリズム#
Xiaolin Wuのアルゴリズムは、線分上でx座標、y座標のいずれかが整数、もう一方が実数で表されていると仮定する。ここでは \(| x_1 - x_0| > | y_1 - y_0 |\) かつ \(x_0 < x_1\) の場合を考えよう。
この場合、前述の直線描画のアルゴリズムにおいてx座標は1ずつ増加し、y座標は直線の傾き分だけ増加するのであった。従って、x座標は整数、y座標は実数というXiaolin Wuのアルゴリズムの仮定が成り立つ。
これまでは塗りつぶす画素の座標をy座標の実数値を四捨五入することで決定していたが、Xiaolin Wuのアルゴリズムでは、y座標の実数値を整数部 \(y_\text{n} = \lfloor y \rfloor\) と小数部 \(y_\text{d} = y - y_\text{n}\) に分ける。この際、小数部は本来塗りつぶすべき位置が、格子点に対してどれだけずれているかを表す。小数部が0であれば、これまで通り点 \((x, y_\text{n})\) に対応する格子点を黒く塗りつぶせば良いし、小数部が限りなく1に近ければ、 \((x, y_\text{n} + 1)\) の格子点を黒く塗りつぶすことになる。
このように考えると、 \(y_d\) の値が0から1に変化していくにつれ \((x, y_\text{n})\) と \((x, y_\text{n} + 1)\) に描画する色の濃さを線形に変化させていけば良さそうだ。より具体的には、背景の色を \(C_{\text{bg}}\), 線の色を \(C_{\text{fg}}\) として、次の式に描画色 \(C\) を決定すれば良い。
この式を用いて、前述の線分の描画プログラムの該当箇所を更新する。
# 直線を描画
for i in range(n + 1):
x = x0 + i * dx
y = y0 + i * dy
if dx == 1.0:
# y方向に線を拡張
x = int(x + 0.5)
yi = int(y)
yd = y - yi
image[yi, x] = (1.0 - yd) * FG_COLOR + yd * BG_COLOR
image[yi + 1, x] = yd * FG_COLOR + (1.0 - yd) * BG_COLOR
else:
# x方向に線を拡張
y = int(y + 0.5)
xi = int(x)
xd = x - xi
image[y, xi] = (1.0 - xd) * FG_COLOR + xd * BG_COLOR
image[y, xi + 1] = xd * FG_COLOR + (1.0 - xd) * BG_COLOR
すると、次のようにジャギーが低減された直線が描画される。
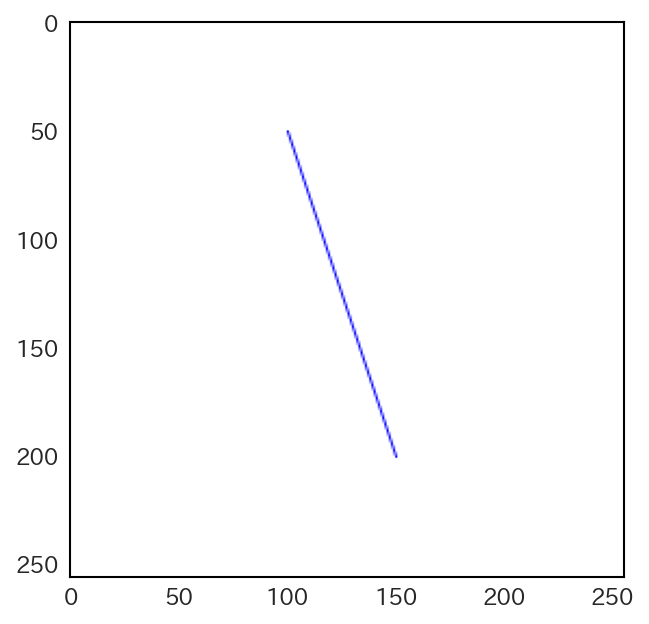
図 1.4 Xiaolin Wuのアルゴリズムによる直線の描画結果#
1.3.3. 円の描画#
円の描画にはいくつかの方法があり、最も単純には、円を正多角形と見なし、前述の線分描画のアルゴリズムをもいて描画すれば良い。
一方で、円の関数を直接的に評価して描画する方法もある。先ほどの線分描画のアルゴリズムでは、描画する線分の傾きが1以下になるようにx座標を1画素ずつ動かすのか、y座標を1画素ずつ動かすのかを切り替えていた。
円にこの考え方を当てはめると、円周を八等分して、各45度分の円弧をx座標、y座標のいずれかを1画素ずつ動かしながら描画する方法が考えられる。
import numpy as np
import matplotlib.pyplot as plt
SIZE = 256 # 画像のサイズ
BG_COLOR = np.array([255, 255, 255], dtype=np.uint8) # 背景の色
FG_COLOR = np.array([0, 0, 255], dtype=np.uint8) # 線の色
# 円の中心座標と半径
CX = 128
CY = 128
RADIUS = 100
# 背景が白の画像を作成
image = np.full((256, 256, 3), BG_COLOR, dtype=np.uint8)
# 円を描画
x = RADIUS
y = 0
while x >= y:
# 第1円弧の点に対応する8点を一度に描画する
image[CY + y, CX + x] = FG_COLOR
image[CY + y, CX - x] = FG_COLOR
image[CY - y, CX + x] = FG_COLOR
image[CY - y, CX - x] = FG_COLOR
image[CY + x, CX + y] = FG_COLOR
image[CY + x, CX - y] = FG_COLOR
image[CY - x, CX + y] = FG_COLOR
image[CY - x, CX - y] = FG_COLOR
# 座標の更新
y += 1
x = np.sqrt(RADIUS * RADIUS - y * y)
x = int(x + 0.5)
# 画像を表示
fig, ax = plt.subplots()
ax.imshow(image, vmin=0, vmax=255, interpolation=None)
ax.grid(False)
plt.show()
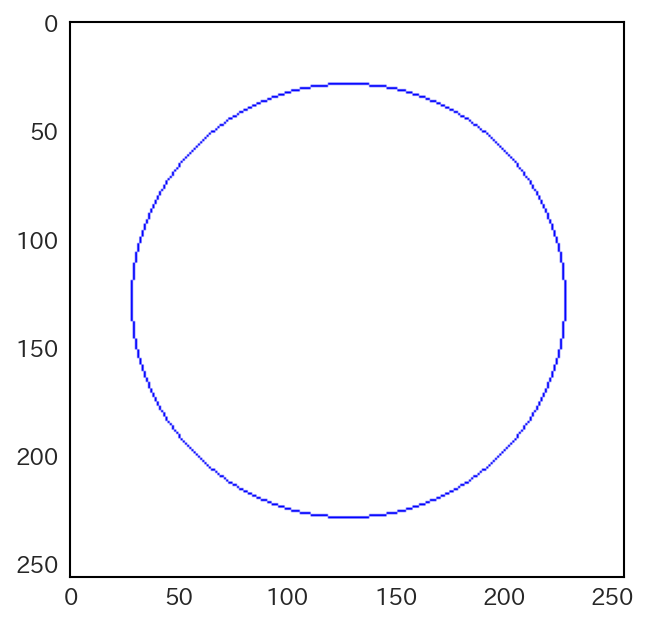
練習問題
前述の円の描画アルゴリズムにXiaomin Wuのアルゴリズムを組み合わせて、アンチエイリアシングされた円を描画するプログラムを作成せよ。
1.3.4. Bézier曲線#
関数を用いて、より自由な曲線を描くには、一定の次元の多項式を用いることが多い。その中で、最も広く用いられているものは三次の多項式を用いる三次 Bézier曲線 である (注意: Bézier曲線自体は任意の次数を用いることができる)。
Bézier曲線を定義するには次数+1個の点を用いる。三次のBézier曲線であれば、4つの点が用いられる。これらの4点は制御点 (control point)と呼ばれ、始点から終点に至る曲線の形状を制御するのに用いられる。
三次Bézier曲線の定義に用いられる4点の座標を\(\mathbf{p}_0, \mathbf{p}_1, \mathbf{p}_2, \mathbf{p}_3\)と表す。これらを用いて、始点 \(\mathbf{p}_0\) と終点 \(\mathbf{p}_3\) を通る曲線を表す時、\(t = 0\)が始点、\(t = 1\)が終点に対応するようなパラメータ \(t\)を用いて曲線上の点を定義する。
この式は、\(\mathbf{p}_0, \ldots, \mathbf{p}_3\) の隣り合う点をパラメータ \(t\)で階層的に線形補間することで得られる。すなわち、
という中間点を生成し、更に、
と線形補間を繰り返すと、 (1.1) が得られる。
従って、Bézier曲線をラスタ化するには、tを0から1の間で少しずつ増やしていき、得られる2点の間に順々に線分を描いていけば良い。このような描画のアルゴリズムを de Casteljauのアルゴリズム と呼ぶ (de Casteljauは「ド・カステリョ」と読む)。
本アルゴリズムを用いてBézier曲線を描くプログラムの「結果」を次に示す。以下の描画結果では制御点を動かして、曲線の形を変更することができるので各自試してみてほしい。
有限次元のBézier曲線を用いて、より複雑な曲線を描くには、安直には曲線の次数を上げれば良いように思われるが、この方法では表せる曲線に限界がある。従って、実用的には、複雑な曲線の一部の区間を三次などの低次のBézier曲線で表し、それらを繋げることで描画される。
また、Bézier曲線には、円弧を正しく表すことができない、という重要な制約がある。Bézier曲線は、あくまで多項式で表せる曲線を描画するが、周知の通り、円弧は有限次元の多項式で表せない曲線である。
別の見方をすると、円は常に曲率が一定の曲線である。Bézier曲線の曲率は曲線のパラメータ \(t\)に関して、点の座標を2階微分することで得られるが、これが \(t\)に依らず定数になるのは、Bézier曲線の次数が1のときだけで、この場合は直線を表すに過ぎない。
ただし、Bézier曲線の定義式において、多項式を分母と分子に持つような拡張である 有理Bézier曲線 (rational Bézier curve) を用いることで、円弧を表すことができる。一例として二次の有理Bézier曲線は、次のような一般式で表すことができる。
ここで、\(w_0\), \(w_1\), \(w_2\)はそれぞれの点に対応する重みである。実際に円をパラメータ表示しようとする場合、 \(t = \tan \frac{\theta}{2}\) を用いると、単位円上のx座標とy座標は次のように表せる。
この式から、有理Bézier曲線を用いれば円弧を正しく表せることが確認できる。
練習問題
三次の有理Bézier曲線を用いて四分円を描画するには、次の4点を制御点として用いれば良い。
実際にプログラムを作成し、この4点を用いた有理Bézier曲線が四分円と一致することを確かめよ。
