物体検出

5. 物体検出#

参考資料

  • 『ディジタル画像処理 改定第二版』 P.233 第11章 パターン・図形・特徴の検出とマッチング

5.1. テンプレート・マッチング#

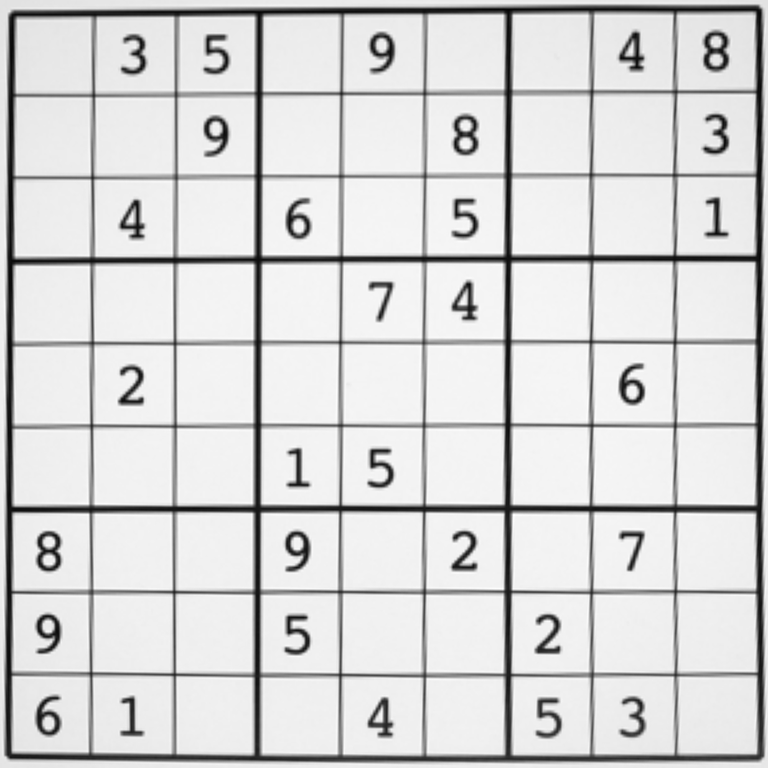
テンプレート・マッチングとは、とある画像の中に、特定のパターンを持つテンプレート画像と似た画像を探す技術である。以下では、次の数独問題の画像から特定の数字がどこに存在するかをテンプレート・マッチングにより探索する問題について考えてみよう。

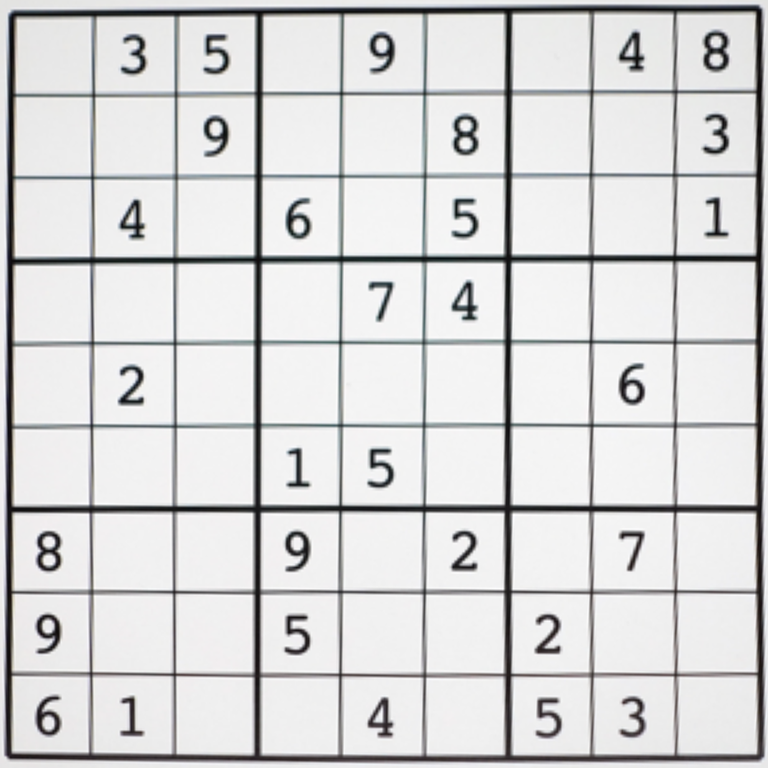
../_images/sudoku_rectified.png

図 5.1 本項で扱う数独問題の画像#

今回はテンプレートとして、以下の「1」, 「2」, 「3」 の数字が書かれた画像を用意した。

表 5.1 本項で用いるテンプレート画像#

1

2

3

以下ではまずテンプレート・マッチングに用いられる画像同士の類似度指標について見ていく。

5.1.1. 画像の類似度#

画像の特定の領域がテンプレート画像と一致するかどうかを調べたい場合、単純には画像と画像の差を考えればよいだろう。このような画像の差や類似度としては二乗誤差和 (SSD, sum of squared differences)や絶対誤差和 (SAD, sum of absolute difference) がある。2つの大きさが等しい画像 \(I\) と \(J\) のSSDならびにSADは次の式で計算できる。

\[\begin{split} \begin{align*} D_\text{SSD}(I, J) &= \sum_{x,y} (I(x,y) - J(x,y))^2 \\ D_\text{SAD}(I, J) &= \sum_{x,y} |I(x,y) - J(x,y)| \end{align*} \end{split}\]

これらの指標は、画像 \(I\) と \(J\) をベクトルとして見なしたときには、それぞれL2ノルムとL1ノルムに対応している。

SSDやSADは値が小さくなるほど画像同士が似ていることを示す距離指標だが、反対に値が大きいほど画像同士が似ていることを表す類似度指標もある。その代表例が 正規化相互相関 (NCC, normalized cross-correlation) である。NCCは次の式で計算できる。

\[ D_{\text{NCC}}(I, J) = \frac{\sum_{x,y} I(x,y) J(x,y) }{\sqrt{\sum_{x,y} I(x,y)^2 \sum_{x,y} J(x,y)^2}} \]

NCCは、画像 \(I\) と \(J\) をベクトルと見なした場合には、二つのベクトルがなす角に対する余弦を表している。

数独問題の画像上から「2」のテンプレートに近い画像領域を検索した結果を以下に示すが、SSD (を0-1の範囲の類似度になるように正規化したもの)は、0-1の範囲で様々な値を取るのに対して、NCCは全体的に1に近い値を取る傾向があることが分かる。ただし、NCCの結果の最小値と最大値が0-1の範囲になるように再度正規化すると、実質的な差はほとんどないことが分かる。

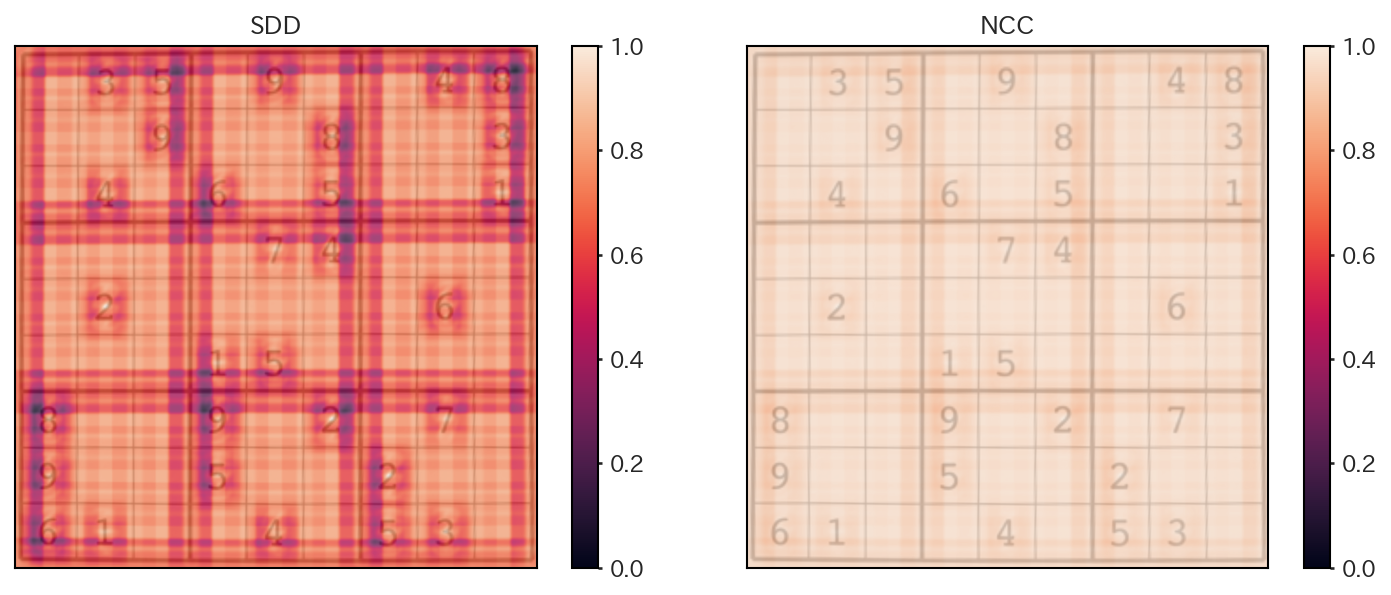
../_images/9ba54b8a3b98e7a1a9232decb6414f630e7f2720597521fbe7bb4f9d025d9636.png

図 5.2 SDD/NCCによるテンプレートと画像の類似度#

また正規化相互相関と類似した手法には画像を表すベクトル \(I\) と \(J\) の間でPearsonの相関係数と同様の値を計算する ゼロ平均正規化相互相関 (ZNCC, zero-mean normalized cross-correlation) がある。ZNCCはPearsonの相関係数と同様に次の式で計算できる。

\[ D_{\text{ZNCC}}(I, J) = \frac{\sum_{x,y} (I(x,y) - \bar{I})(J(x,y) - \bar{J})}{\sqrt{\sum_{x,y} (I(x,y) - \bar{I})^2 \sum_{x,y} (J(x,y) - \bar{J})^2}} \]

ここで \(\bar{I}\) は画像 \(I\) の平均値、\(\bar{J}\) は画像 \(J\) の平均値である。ZNCCは画像の平均値を引き算して輝度を調整するため、画像の明るさの際に関する影響を受けづらい。

NCCとZNCCの比較を以下に示すが、ZNCCの方が、テンプレートがマッチする箇所でより周囲から際立って高い類似度を示すことが確認できる。

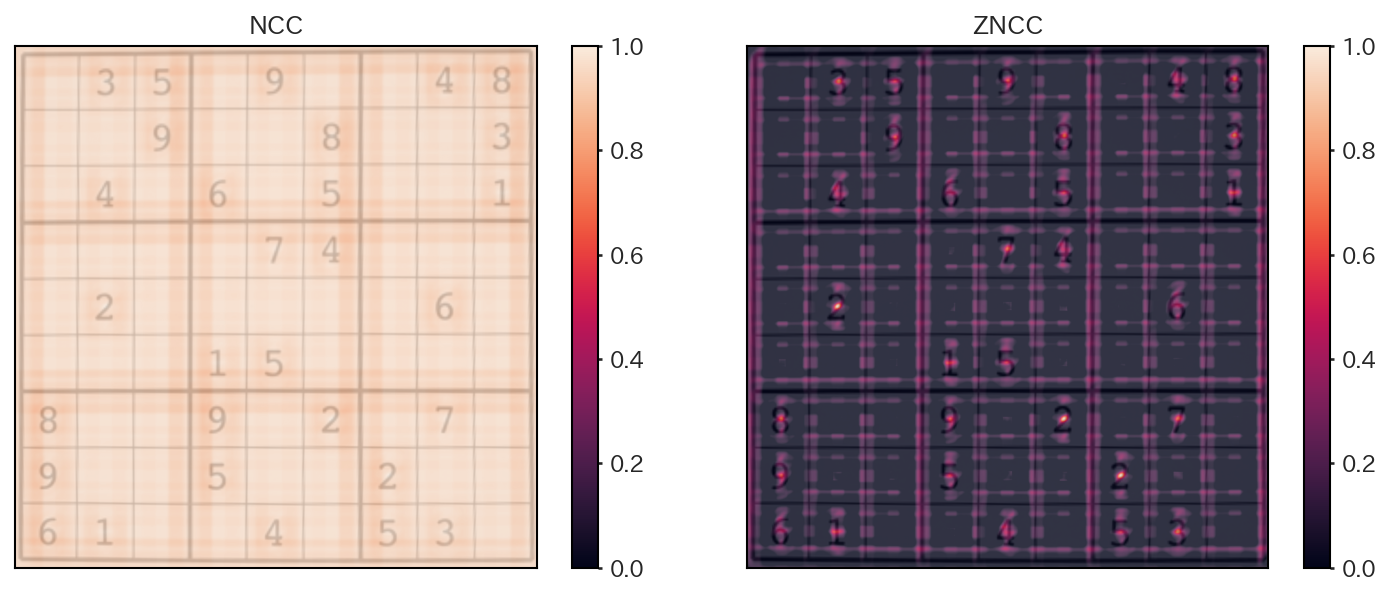
../_images/0ec1083743179e40ef9ab5bf58a026e734292976dcb407404252d0d70c232bb0.png

図 5.3 NCC/ZNCCによるテンプレートと画像の類似度#

ここまで、テンプレート画像との厳密な一致を目的とした類似度指標について紹介してきたが、応用をテンプレート・マッチングに限らなければ、非常に多くの画像類似度手法が存在する。

例えば、画像同士が人間の知覚において類似しているかどうかを表す手法に 構造化類似度 [12] (SSIM, structural similarity) がある。SSIMは、画像の輝度、コントラスト、構造という人間が知覚的に類似度を判断するのに重要視するであろう要素を元にして、次の式で計算される。

\[ D_{\text{SSIM}}(I, J) = \frac{(2 \bar{I} \bar{J} + c_1)(2 \text{Cov}(I, J) + c_2)}{(\bar{I}^2 + \bar{J}^2 + c_1)(\sigma(I)^2 + \sigma(J)^2 + c_2)} \]

本式で、\(\bar{I}\), \(\bar{J}\) は画像 \(I\), \(J\) の平均画素値を、\(\sigma(I)\) ならびに \(\sigma(J)\) は二つの画像それぞれの輝度の標準偏差を、\(\text{Cov}(I, J)\) は二つの画像の輝度値の共分散をそれぞれ表す。この式は、元々は輝度 (luminance)、コントラスト (contrast)、構造 (structure)に対応する次の3つの式の積として定義されている。

(5.1)#\[\begin{split} \begin{align*} l(I, J) &= \frac{2\bar{I} \bar{J} + c_1}{\bar{I}^2 + \bar{J}^2 + c_1} \\ c(I, J) &= \frac{2\sigma(I) \sigma(J) + c_2}{\sigma(I)^2 + \sigma(J)^2 + c_2} \\ s(I, J) &= \frac{\text{Cov}(I, J) + c_3}{\sigma(I) \sigma(J) + c_3} \end{align*} \end{split}\]

なお、\(c_1\), \(c_2\), \(c_3\) はパラメータで、多くの場合 \(k_1 = 0.01\), \(k_2 = 0.03\), \(L\)を一つの画素が表せる画素値の階調数 (8ビットなら255)を用いて、\(c_1 = (k_1 L)^2\), \(c_2 = (k_2 L)^2\), \(c_3 = \frac{c_2}{2}\) のように定義される。

(5.1) で、輝度成分の\(l(I, J)\) は二つの画像の平均値の差を見ている。一目にはこの式が差を表しているようには見えないかもしれないが、この式は相加平均と相乗平均の関係式を変形することで導かれ、平均値が一致するときに1を取るような類似度指標となっている。

コントラストの成分 \(c(I, J)\) も同様の考え方によって定義されており、こちらは、画像の持つ輝度の標準偏差の類似度を見ることで、画像中に存在する輝度のバリエ－ション (≒ コントラスト)がどのくらい似ているかを評価している。最後の構造の成分 \(s(I, J)\) は多少形は異なるものの、おおよそZNCCの定義と同じになっていて、輝度やコントラストの差異を取り除いた上での画像の類似度を評価している。

SSIMはテンプレート・マッチングの文脈で用いられることは、それほど多くはないが、画像の品質の評価が必要な様々な場面で用いられる代表的な手法であるので、覚えておくと良いだろう。

この他、近年ではAlexNetやVGG等の深層ニューラルネットワークの出力する中間層の特徴から計算される LPIPS [13] (learned perceptual image patch similarity) のような指標も、画像の類似度評価に広く使われている。

まとめ: テンプレート・マッチングのための類似度指標

  • テンプレート・マッチングにはSADやSSDなどのように、画像の断片をベクトルと見立てた際の距離指標が使われる

  • Pearsonの相関係数に基づくZCNNは、画像の明るさの影響を受けづらく、より構造的な類似度を図ることができる

  • また、テンプレート・マッチングとは別に、画像の類似度には知覚的な要素を考慮したSSIMや深層学習器を用いるLPIPSのような指標もある

練習問題

2つの画像のSSIMはscikit-imageに実装されている skimage.metrics.structural_similarity を使うと計算できる。画像にノイズを付加する、明るさを変えるといった操作を加えた際に、SSIMがどのように変化するかを確認せよ。

5.1.2. Chamferマッチング#

ここまでに紹介したZNCC等によるテンプレート探索は、入力画像上のすべての位置に対してテンプレート画像との距離を求める必要があった。この処理は、並列計算などにより高速化できる余地があるものの、画像のサイズが大きくなると、それに応じて計算量が膨大になってしまう。

本項で紹介する Chamferマッチング は、入力画像とテンプレート画像のそれぞれを距離画像とエッジ画像として表現し直すことにより、テンプレートをある初期位置からどの方向にどれだけ動かせば、最もマッチする位置に到達するかを逐次計算し、テンプレート位置を最適化する手法である。

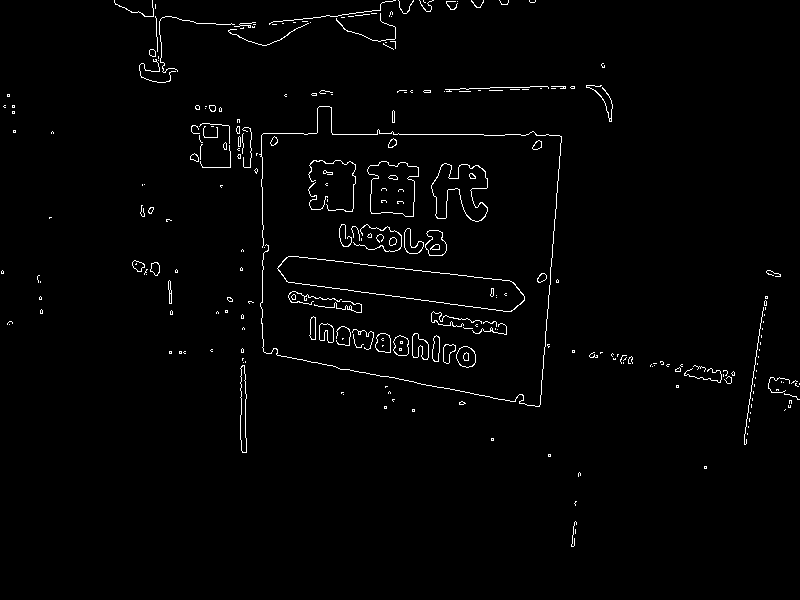
Chamferマッチングを行うためには、いわゆる 距離画像 の事前計算が必要となる。距離画像は以下の表 5.2 に示すように入力画像からCannyエッジ検出により1画素幅のエッジを取得した後、そのエッジからの最短距離を各画素から計算することで得られる。

表 5.2 距離画像の計算#

入力画像

Cannyエッジ検出

距離画像

../_images/374feed78483e8cbe89b03ec4debbd0441e4020c134f43d1f0eafbad21b19b4b.png

../_images/abd1cd9efbe6dce34a8363faee14d8db2fc4d0a247e39beadd830ac5c45c1dfc.png

../_images/b8f2f68c98d56816c7b839e360f8e8d18ad30a569448c516bdc401d676e973ba.png

今、入力画像 \(I\) の距離画像を \(I_{\text{DT}}\) とし、テンプレート画像 \(T\) のエッジ画像を \(T_{\text{E}}\) と表すことにしよう。この表現を用いる場合、テンプレート画像を入力画像上の位置 \((x, y)\) に配置したときの類似度 \(S(x, y)\) は次の式で表せる。

\[ S(x, y) = \sum_{x', y'} T_{\text{E}}(x', y') I_{\text{DT}}(x + x', y + y') \]

ただし、\(x'\), \(y'\) はテンプレート画像の画素の位置全体を動くものとする。この指標はテンプレート画像のエッジが、入力画像の距離画像上で「よりエッジに近い位置」に来るほど値が小さくなる。この関数を最小化する位置 \((x, y)\) を求めるために、Chamferマッチングでは \(S(x, y)\)の \(x\), \(y\) に関する偏微分を考える。

\[\begin{split} \begin{align*} \frac{\partial S}{\partial x} &= \sum_{x', y'} T_{\text{E}}(x', y') \frac{\partial I_{\text{DT}}(x + x', y + y')}{\partial x} \\ \frac{\partial S}{\partial y} &= \sum_{x', y'} T_{\text{E}}(x', y') \frac{\partial I_{\text{DT}}(x + x', y + y')}{\partial y} \end{align*} \end{split}\]

この式に現れる \(I_{\text{DT}}\) の偏微分は距離画像のエッジのようなもので、事前計算可能である。これらの偏微分の値を用いて、最急降下法の要領で \(S(x, y)\) を最小とするようなテンプレートの位置 \((x, y)\) を求めるのである。

Chamferマッチングは、SSDやZNCCなどの類似度手法を用いる場合と異なり、全ての \((x, y)\) に関するマッチングは不要で、適当な初期位置を与えることができれば、そこから勾配法により最適なテンプレート位置を決定できる。

以下に100個の適当な初期点からChamferマッチングを実行した結果を示す。

../_images/0d79a5f58d1d495d7398709a0c0bc573444b99de060363b25fe4f413cd94817d.png

図 5.4 Chamferマッチングの結果#

この結果を見てみると、いくつかの初期点からスタートして正しく「2」のマスの中央に到達している軌跡があることが確認できる。

その一方で、テンプレートの初期位置が適当でない場合には、局所解として不適切な位置でテンプレートが滞留する可能性もある。このような問題を防ぐため、入力画像とテンプレート画像の解像度を落とした画像における全探索等で初期位置のあたりを付けておき、有効と考えられる初期点に対して、元の画像サイズでChamferマッチングを行う、といった処理が一般的である。

まとめ: Chamferマッチング

  • Chamferマッチングは距離画像とエッジ画像を用いて、テンプレート位置を再急降下法の要領で最適化する方法である

  • Chamferマッチングは前述のテンプレート・マッチングと異なり、全画素に対してのマッチングが不要である

  • その一方、Chamferマッチングの結果は初期のテンプレート位置に強く依存するため、良い初期位置を与えるための工夫が必要である

5.2. Hough変換による図形の検出#

5.2.1. Hough変換#

Hough変換とは 1962年にPaul Houghが提案した、画像中の特定の図形を検出するアルゴリズムである。Hough変換は、特に直線や円などの少ないパラメータで記述可能な図形を検出するために広く用いられている。

Hough変換は、画像中のエッジを検出し、それらのエッジがどのような図形を形成しているかを解析することで、図形の位置や形状を特定する。そのエッジ上の各点 \((x_i, y_i)\) について、その点を通る直線の集合を考える。そのような直線は \(y = \hat{a} x + \hat{b}\) のような形で表せる (画像上の座標と、パラメータを区別するため、パラメータには \(\hat{a}\) のようにハット記号をつける)。また、\(\hat{a}\)について、\(\hat{b}\)は \(\hat{b} = y_i - \hat{a}x_i\) という直線の式で表せる・

したがって、直線のパラメータ \((\hat{a}, \hat{b})\) に関する二次元座標系(以後、「パラメータ座標」と呼ぶ) で、 \((x_i, y_i)\) を通る直線の集合は、\(\hat{b} = - \hat{a}x_i + y_i\) という直線として表せる。反対に、\(\hat{a}\)-\(\hat{b}\) 空間における点 \((\hat{a}, \hat{b})\) は画像上では1つの直線に対応している。

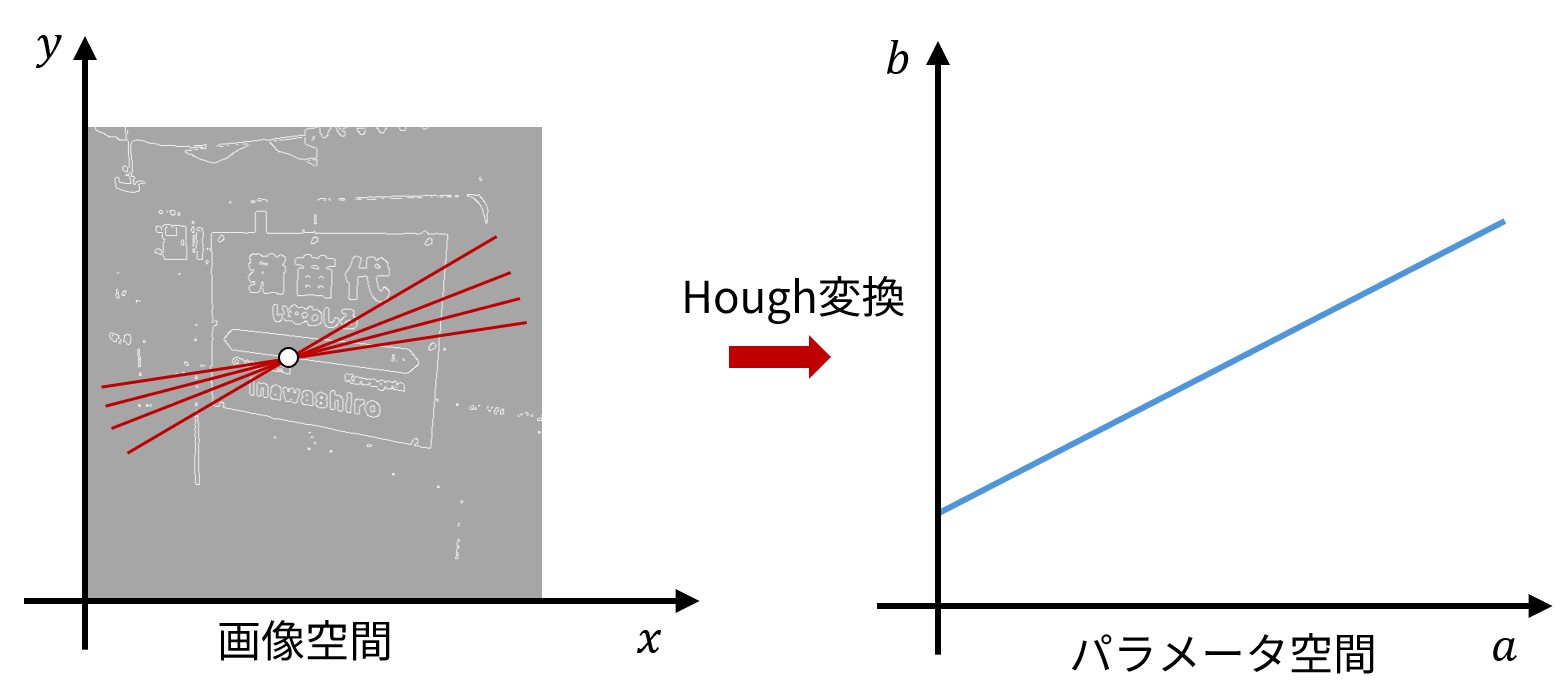
../_images/hough_transform.jpg

図 5.5 Hough変換の概念図#

反対に、画像上のエッジにある各 \((x_i, y_i)\) について \(\hat{a}\)-\(\hat{b}\) 空間直線を引くと、画像上に存在する直線に対応する点 \((a, b)\) で多くの直線が交わる (エッジと直線の言葉遣いの違いに注意すること)。以上のようにHough変換は、

  • 画像上の点をパラメータ空間の直線に写す

  • パラメータ空間上の点を画像上の直線に写す

という効果を持つ。

計算機上でHough変換を実装するためには、一定の区間の \((\hat{a}, \hat{b})\) を有限個のセルに分割しておく。その上で、\(\hat{a}\)-\(\hat{b}\) 空間上で直線が通るセルに投票を行っていき、票数が多いセルに対応する \((\hat{a}, \hat{b})\) が画像上で直線を形成しているとみなす。

実装上の問題#

しかし、直線の検出のために \((\hat{a}, \hat{b})\) というパラメータを用いる場合、理論的には \((\hat{a}, \hat{b})\) が実数全体の値を取りうるにも関わらず、それを有限区間に限定した上で、さらにセルに分割しなければならない、という問題がある。

実際、画像の中に存在する直線が一定の区間の \((\hat{a}, \hat{b})\) に収まっている保証はなく、また、パラメータ空間のより広い範囲を扱おうとする場合には、 セル上の値を保持するために多くのメモリを消費する ことになる。従って、\(\hat{a}\)-\(\hat{b}\) 空間上を有限個のセルに分割するというのは実質的に不可能である。

このような問題を解決するため、直線検出においては、 \((\hat{a}, \hat{b})\) とは異なるパラメータで直線を表現することが多い。例えば、直線の方程式を

(5.2)#\[ \hat{\rho} = x \cos \hat{\theta} + y \sin \hat{\theta} \]

とおいて、Hough変換に用いるパラメータ空間を \((\hat{\rho}, \hat{\theta})\) で表す場合を考えよう。ここで \(\hat{\rho}\) は原点と直線の「符号付き」距離を表し、 \(\hat{\theta}\) は原点から直線に下ろした垂線の傾きを表す (図 5.6 を参照)。

なお、ここで言う「符号付き距離」とは、直線と原点から直線に下ろした垂線の交点 \(H\) が第一象限あるいは第二象限にある場合に正、第三象限あるいは第四象限にある場合に負の値を取るような距離である。

このようなパラメータを用いるHough変換を提案者の名前から Duda-HartのHough変換 と呼ぶ。

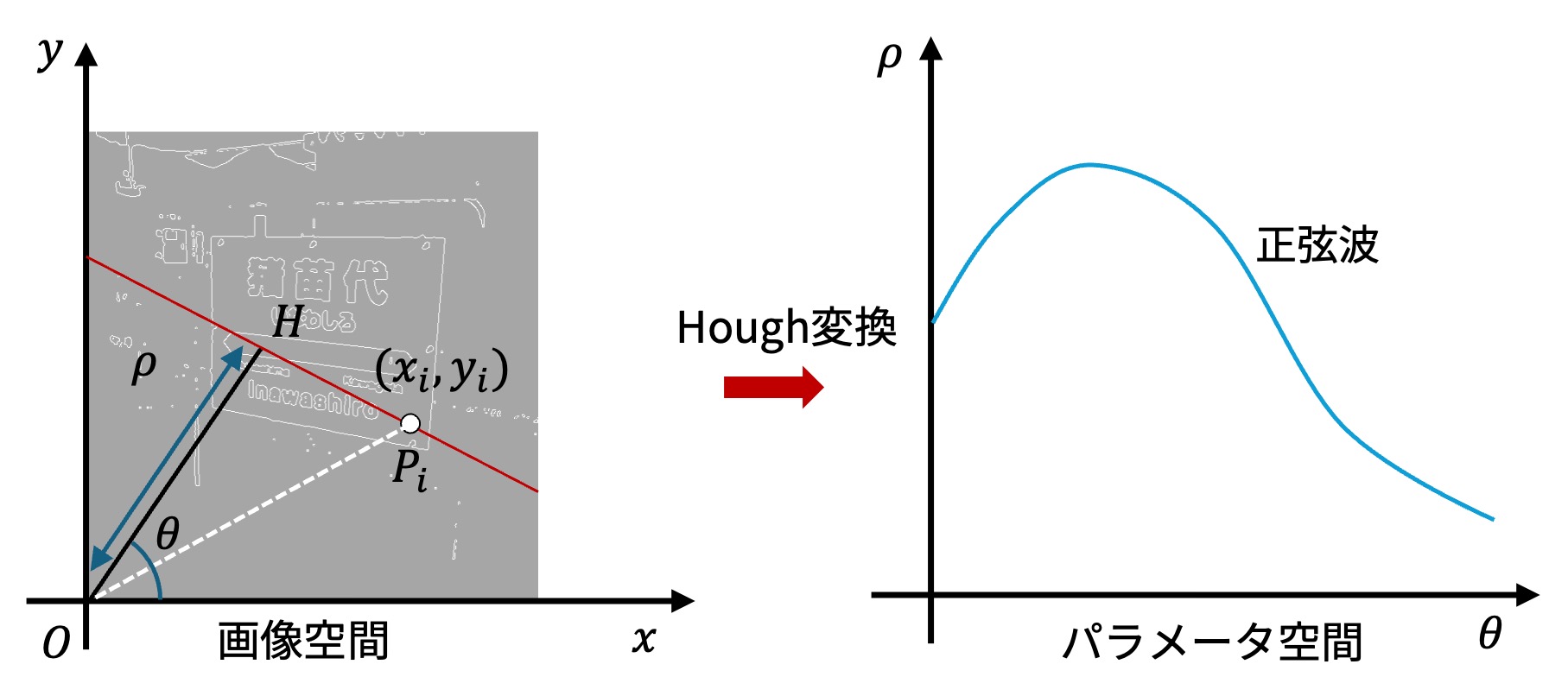
../_images/hough_transform_2.jpg

図 5.6 直線の原点からの距離と傾きを用いたHough変換#

この際、原点との符号付き距離 \(\hat{\rho}\) は画像の対角線の長さを \(L\) として、\([-L, +L]\) という有限の範囲に収まっている。また、直線の傾き \(\hat{\theta}\) も \([0, \pi]\) という有限の範囲に収まる。したがって、この区間を有限のセルで分割すれば、任意の画像上の直線がパラメータ空間の中に収まることが保証される。

結論から言うと、画像上の一点を通る直線の集合は、\((\hat{\rho}, \hat{\theta})\) を用いたパラメータ空間上では正弦波を描く。この事実を確かめてみよう。

図 5.6 において、y軸と直線 \(OP_i\)がなす角度を \(\phi\) と置くと、

\[ \phi = \cos^{-1} \left( \frac{y_i}{\small\sqrt{x_i^2 + y_i^2}} \right) \]

と書ける。すると、\(\angle P_i OH\) は \(\hat{\theta} + \phi - \frac{\pi}{2}\) と書ける。従って、 \(D = \sqrt{x_i^2 + y_i^2}\) として、\(\hat{\rho}\) を表すと、

\[ \hat{\rho} = D \cos(\hat{\theta} + \phi - \frac{\pi}{2}) = D \sin (\hat{\theta} + \phi) \]

と書ける。このことから、パラメータ \((\hat{\rho}, \hat{\theta})\) を用いると、画像上の一点はパラメータ空間上の正弦波に変換されることが分かる。

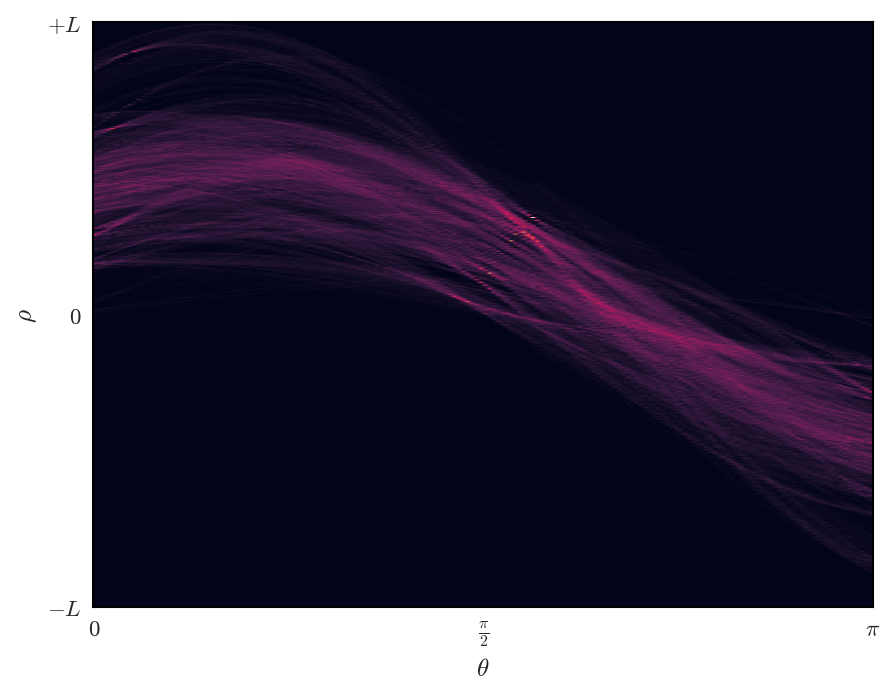
Duda-HartのHough変換を手法を用いて画像上から直線を検出した結果を以下に示す。

表 5.3 Hough変換の結果#

入力画像

Cannyエッジ検出

../_images/a1f219b645f1edc4255c7a580b075680e1e65af6af4b1e199cbf2a47d3cec0c0.png

../_images/b2a8e9d712e7621a5a0234c6d12c855957348f1b607308466fe4ed76dd6c1110.png

パラメータ空間の投票数分布

Hough変換

../_images/3c54bc76d6e8a00fb99cd2807c210c2921ef8e4167d3310bdf583e0806ff68fa.png

../_images/d376f326e24277f2fa21d3ef12b1fae6fbad285654b8820da8144e78e26b0a5a.png

結果から分かる通り、Hough変換により、エッジ上の各点が正弦波を描き、パラメータ空間上で多くの曲線が交わる箇所が点在していることが確認できる。このうち一致以上の投票数を集めたものを画像空間で描画したものが右下の画像で、検出された直線が画像のエッジ上を通っていることが分かる。

5.2.2. ランダム化Hough変換#

ここまでに紹介した通常のHough変換は、エッジ上のすべての点についてパラメータ空間上での直線や正弦波を描画する必要があり、入力画像の大きさや、パラメータ空間の分解能に応じて計算量が増大するという問題がある。しかも、このようなパラメータ空間上に描画される正弦波等の上の点は、ほとんどが画像上に存在しない図形に対応しており、計算的にも無駄が多い。

また、図形のパラメータ数も、直線なら2つで済むが、円ならば3つ、楕円ならば5つとパラメータ空間の次元が増えることも、Hough変換の計算量を増大させる原因である。

このような問題を防ぐために、ランダム化Hough変換では、パラメータを \(n\) 個持つ図形を検出するために、\(n\) 点をランダムに選び、その \(n\) 点から決まる図形のパラメータに対応する パラメータ空間上の1点のみ に投票を行う。

この操作は、エッジ上の点をランダムに \(n\) 個選ぶ操作を繰り返すだけなので、精度とのトレードオフはあるものの、画像のサイズやパラメータ空間の分解能、パラメータ空間の次元等に依存せず、一定の計算量を保つことができる。

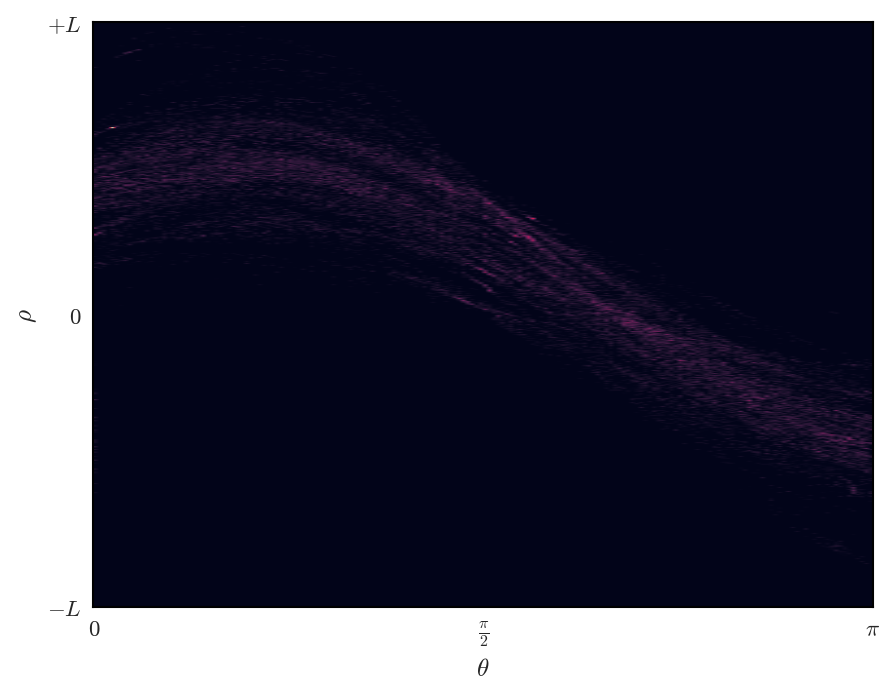
以下に、ランダム化Hough変換によるパラメータ空間上の投票数と、直線の検出結果の例を示す。

表 5.4 確率的Hough変換の結果#

パラメータ空間の投票数分布

Hough変換

../_images/9e1e7fbcd0867620723c6664b1729795e754c4b63d4251e9992ab69c2493e3c0.png

../_images/91b29ed42aeca494a84b2a01cae574c00de21bfa9b371eac8c143acdc8cc04ba.png

なお、上記の例では、従来のHough変換において直線のパラメータを求める操作をランダムに選んだ2点から決めるという変更に留めたが、実際のランダム化Hough変換では、Houghテーブル上に投票数の他、近似される線分のパラメータの保持・更新を行うなど、もう少し複雑な処理を行っている。

このあたりの詳細に興味のある読者は、文献 [14] を参照してほしい。

5.2.3. 一般化Hough変換#

ここまでに紹介したHough変換は、直線や円などのように、一定数のパラメータによって図形が定義されるような図形を検出する方法であった。

しかし、より一般的な図形を表すためには、パラメータ数をさらに増やす必要も生じるほか、そもそもパラメータによって上手く表すことができない図形もあるだろう。

このような場合に用いられるのが一般化Hough変換である。一般化Hough変換では、図形を表すために、図形の姿勢を表すパラメータとして並進ベクトル \((t_x, t_y)\), 回転角度 \(\theta\), スケール \(s\) の4つを用いる。

さらに、図形自体の表現を輪郭線上の点の集合として表す。図形上の点を \(\mathbf{x}_i = (x_i, y_i)\) としたとき、各点で次の2つの値を計算しておく。

  • \(\mathbf{x}_i\) から図形上の基準点 (例えば重心) に向かうベクトル \(\mathbf{v}_i\)

  • \(\mathbf{x}_i\) におけるエッジの傾き \(\psi_i\)

この時、各 \(\mathbf{v}_i\) は、\(\mathbf{v}_i = (r_i \cos \alpha_i, r_i \sin \alpha_i)\) のように2つのパラメータ \((r_i, \alpha_i)\) で表しておく。

このようにして得られた各点のパラメータは \((r_i, \alpha_i, \psi_i)\) の3つのパラメータで表されるが、ここで、エッジの向き \(\psi_i \in [0, \pi]\) を量子化して \(N\) 個のビンに分けておく。すると、\(\psi_1, \ldots, \psi_N\) の各ビンに対して、\((r_i, \alpha_i)\) の値を格納した形状定義表を作ることができる。

この形状定義表を用いると、任意の形状に対してHough変換を行うことができる。具体的には、画像上の点 \((x, y)\) に対して、次のような処理を行う。

投票先の計算は、全ての取りうる \((\theta, s)\) に対して \((t_x, t_y)\) の値を計算することで行われる。今、図形の傾きが \(\theta\) であると考えると、傾ける前のエッジの向きは \(\psi - \theta\) であるので、この値に対応する \((r_j, \alpha_j)\) の値を全て取り出す。

基準点が原点であるとき、変形前の図形上点 \((x_i, y_i)\) は、その定義から

\[\begin{split} \begin{align*} x_i &= -r_j \cos(\alpha_j) \\ y_i &= -r_j \sin(\alpha_j) \end{align*} \end{split}\]

と書けるのだった。この点を、回転、スケール、並進の順で座標変換すると、変形後の図形上の対応点 \((x'_i, y'_i)\) は次のように表せる。

\[\begin{split} \begin{align*} x'_i &= - s r_i \cos(\alpha_j + \theta) + t_x \\ y'_i &= - s r_i \sin(\alpha_j + \theta) + t_y \end{align*} \end{split}\]

したがって、各 \((\theta, s)\) に対して、取りうる並進量 \((t_x, t_y)\) は次のように表せる。

\[\begin{split} \begin{align*} t_x &= x + s r_i \cos(\alpha_j + \theta) \\ t_y &= y + s r_i \sin(\alpha_j + \theta) \end{align*} \end{split}\]

以上のようにして、 \((\theta, s, t_x, t_y)\) に対して投票を行っていくと、通常のHough変換と同様に、任意の図形を検出することができる。

まとめ: Hough変換

  • Hough変換は直線や円など、少数のパラメータで定義される図形を画像中から検出する手法である

  • Hough変換はエッジ上の点を通る全ての図形を、パラメータ空間上の別の図形に移す変換である

  • パラメータ空間上で多くの投票が集まったパラメータが画像上での図形に対応する

  • Hough変換には、計算量を削減するためのランダム化Hough変換や、任意の図形を検出可能な一般化Hough変換などのバリエーションがある

5.3. 動的輪郭法#

物体の輪郭線を閉曲線として検出する古典的な手法には 動的輪郭法 (active contour method) がある。

動的輪郭法の代表的な手法は、いずれも1988年に提案された Snakes法 [15] と レベルセット法 [16] の2つである。ただし、レベルセット法が画像中の輪郭線検出に応用されたのは少し後で、1997年のことである [17] 。

5.3.1. Snakes法#

Snakes法は、初期の輪郭線をエネルギー関数を最小化するように徐々に変形していくことで、画像中の輪郭線にフィッティングする手法である。

Snakes法のエネルギー関数 \(E\) は曲線のパラメータ \(s \in [0, 1]\) に対して連続的に次の式で表される。

\[ E = \int \left[ E_{\text{internal}}(s) + E_{\text{external}}(s) \right] \mathrm{d} s \]

ここで、 \(E_{\text{internal}}\) は曲線そのものの状態から決まるエネルギー関数で、一般的には、曲線の滑らかさを表す関数として次のように定義される。

\[ E_{\text{internal}}(s) = \alpha E_{\text{elas}}(s) + \beta E_{\text{curv}}(s) = \alpha \left| \frac{\mathrm{d} \mathbf{x}(s)}{\mathrm{d} s} \right|^2 + \beta \left| \frac{\mathrm{d}^2 \mathbf{x}(s)}{\mathrm{d} s^2} \right|^2 \]

ここで、第1項は曲線がより短くなる方が低い値を、第2項は曲線がより滑らかな方が低い値を取るようなエネルギーを表す。

また、\(E_{\text{external}}\) は画像のエッジやコントラストなど、画像の状態から決まるエネルギー関数で、一般的には次のように定義される。

\[ E_{\text{external}}(s) = E_{\text{image}}(s) = -\left| \nabla I(\mathbf{x}(s)) \right|^2 \]

この式は、画像のエッジが強いところで曲線が引き寄せられるようなエネルギー関数である。

Snakes法を離散的な曲線に適用するためには、曲線を \(N\) 個の点 \(\mathbf{x}_i\) で近似する。

具体的には、 \(E_{\text{elas}}(s)\), \(E_{\text{curv}}(s)\) ならびに \(E_{\text{image}}(s)\) の式を離散化して、次のように定義する。

\[\begin{split} \begin{align*} E_{\text{elas}}(\mathbf{x}_i) &= \frac{1}{2} \left( \left\| \mathbf{x}_{i+1} - \mathbf{x}_i \right\|^2 + \left\| \mathbf{x}_{i-1} - \mathbf{x}_i \right\|^2 \right) \\ E_{\text{curv}}(\mathbf{x}_i) &= \frac{1}{2} \left( \left\| \mathbf{x}_{i+2} - 2\mathbf{x}_{i+1} + \mathbf{x}_{i} \right\|^2 + \left\| \mathbf{x}_i - 2 \mathbf{x}_{i-1} + \mathbf{x}_{i-2} \right\|^2 \right) \\ E_{\text{image}}(\mathbf{x}_i) &= -\left| \nabla I(\mathbf{x}_i) \right|^2 \end{align*} \end{split}\]

すると、各エネルギーの \(x\) ならびに \(y\) に関する偏微分は次のように表せる。

\[\begin{split} \begin{align*} \frac{\partial E_{\text{elas}}}{\partial \mathbf{x}_i} &= \mathbf{x}_{i+1} - 2\mathbf{x}_i + \mathbf{x}_{i-1} \\ \frac{\partial E_{\text{curv}}}{\partial \mathbf{x}_i} &= \mathbf{x}_{i+2} - 4\mathbf{x}_{i+1} + 6\mathbf{x}_i - 4\mathbf{x}_{i-1} + \mathbf{x}_{i-2} \\ \frac{\partial E_{\text{image}}}{\partial \mathbf{x}_i} &= -2\nabla I(\mathbf{x}_i) \end{align*} \end{split}\]

以下に、この式に従ってSnakes法を実装した結果を示す。

しかし、Snakes法は初期の輪郭線を徐々に変形していくため、2つ以上の図形を一度に検出するなど、輪郭線のトポロジーが途中で変わるような変形を行うことはできない。

5.3.2. レベルセット法#

レベルセット法の元となるアイディアは、初期の曲線 \(C_0\) を徐々に変形させていくことで、別の曲線を表すというものである。

曲線の表現#

ここで曲線 \(C\) が、パラメータを\(p\) とする曲線であって、時刻 \(t\) によって変形するとして \(C(p, t)\) と定義する。ここで、曲線は各時刻 \(t\) において、法線 \(\mathbf{n}(p, t)\) 方向に微小変化するとする。この変化量は曲線の曲率 \(\kappa(p, t)\) の関数 \(F\) で決まるとすると、曲線の関数の時刻 \(t\) における偏微分は

\[ \frac{\partial C(p, t)}{\partial t} = F[\kappa(p, t)] \cdot \mathbf{n}(p, t) \]

この定式化自体はSnakes法のそれと似ているが、この式は曲線が途中で2つに分かれるといったトポロジーの変化を扱うことができない。

そこで、レベルセット法では、曲線 \(C\) を、あるスカラー値関数 \(\phi(x, y, t)\) のゼロ等値面 (zero-level set)として、

\[ C(t) = \{ \mathbf{x} : \phi(x, y, t) = 0 \} \]

のように表すことにする。すると、曲線の変形の式は次のように書き直せる。

\[ \frac{\partial \phi(x, y, t)}{\partial t} = F[\kappa(x, y, t)] \cdot \left| \nabla \phi(x, y, t) \right| \]

レベルセット法を二次元図形の輪郭検出に用いる場合、座標 \(\mathbf{x} = (x, y)\) に加えて、時刻パラメータ \(t \in [0, 1]\) を変数とするスカラー値関数 \(\phi(x, y, t)\) を考える。その上で、 \(\phi(x, y, t) = 0\) となるような点の集合

\[ C(t) = \{ \mathbf{x} : \phi(x, y, t) = 0 \} \]

時刻 \(t = 0\) における輪郭線を \(C_0 = \{ \mathbf{x} : \phi(x, y, 0) = 0 \}\) と定義する。また、\(C_0\) における曲線上の各点での内向きの法線ベクトルを \(\mathcal{N}(\mathbf{x})\) と表すことにする。

ここで、曲線の移動速度を曲線の曲率 \(\kappa(\mathbf{x})\) の関数として \(F[\kappa(\mathbf{x})]\) のように表すとしよう。すると、時刻 \(t\) における曲線の形状は次の式で表せる。

(5.3)#\[ \frac{\partial \phi}{\partial t} = -F[\kappa(\mathbf{x}, t)] \cdot \left| \nabla \phi(\mathbf{x}, t) \right| \]

この定式化を用いると、\(\phi(x, y, t)\) の取り方の如何によって、二次元の輪郭線のトポロジー変化を扱うことができる。

曲線の変形#

レベルセット法では、(5.3) の式を、より具体的に次の式で表す。

\[ \frac{\partial \phi}{\partial t} = g(|\nabla I|) \kappa | \nabla \phi | + \nabla g(|\nabla I|) \cdot \nabla \phi \]

ここで、\(g(|\nabla I|)\) は画像のエッジ強度を表す関数で、エッジストップ関数 (edge stopping function) と呼ばれる。具体的にはエッジからの距離 \(r\) について、\(g(0) = 1\) かつ、 \(\lim_{r \to \infty} g(r) = 0\) となるような関数 (例えばガウス関数) や

\[ g(|\nabla I|) = \frac{1}{1 + (k|\nabla I|)^2} \]

のような関数を用いることが多い (\(k\) はパラメータで最大のエッジ強度の定数倍とすることが多い)。

また、曲線の移動方向 \(\mathbf{n}\) ならびに曲率 \(\kappa\) は、関数 \(\phi\) を用いて次のように表す。

\[\begin{split} \begin{align*} \mathbf{n} &= -\frac{\nabla \phi}{|\nabla \phi|} \\ \kappa &= \mathrm{div} \left( \frac{\nabla \phi}{|\nabla \phi|} \right) \end{align*} \end{split}\]

レベルセット法は \(\phi\) のゼロ等値面を曲線として扱う一方で、関数 \(\phi\) 自体は任意の \((x, y)\) で値を取るので、離散的には初期の\(\phi(x, y, 0)\) を画像のように用意して、各画素 \((x, y)\) における値 \(\phi(x, y, t)\) を徐々に更新していく。

以下に、レベルセット法による輪郭検出の様子と、その際のレベルセット関数の変化の様子を示す。

以上のように、レベルセット法は、仮に初期輪郭が1つの閉曲線であったとしても、2つ以上の図形を検出することができる。ただし、Snakes法と比べると実装が複雑で高速化には多少の工夫が必要になる点は注意が必要である。

まとめ: 動的輪郭法

  • 動的輪郭法は、初期の輪郭線を何らかのエネルギー関数を最小化する形で、画像中の物体の輪郭線にフィッティングする手法である

  • Snakes法は、曲線に関するエネルギー関数を最急降下法の要領で最小化することで物体の輪郭線を検出する

  • レベルセット法は、曲線を高次なスカラー値関数のゼロ等値面として表現することで、複数の図形を同時に検出することができる手法である

目次