8. ステレオビジョン

ステレオビジョンとは、2つの位置が微妙にことなるカメラから撮影された2枚の画像を用いて、画像中の物体の三次元位置を推定する手法である。また、ステレオビジョンのための2枚の画像間の対応点を求めるアルゴリズムをステレオマッチングと呼ぶ。

本設では、ステレオビジョンの理解に不可欠なカメラパラメータとエピポーラ幾何について解説した後に、ステレオマッチングのアルゴリズムとしてのローカル法、グローバル法、セミ・グローバル法について順に紹介する。

参考資料

• 『ディジタル画像処理 改訂第二版』 P.331 第15章 画像からの3次元復元

• 金谷, 菅谷, 金澤, 『3次元コンピュータビジョン計算ハンドブック』 森北出版

8.1. カメラパラメータ

ステレオビジョンを理解する上で「画像」がどのように三次元空間を移しているのかを理解することは重要である。この際、三次元の世界が画像の中にどのように映り込むのかは カメラの持つ性質 に依存することは明らかである。

また、カメラの性質について述べるうえで、各性質が

• カメラというデバイスが持つ性質なのか

• カメラが誰かによって操作されたことによって生じた性質なのか

という違いを理解しておく必要がある。この2つの異なる性質をカメラの 内部パラメータ (intrinsic parameters) と 外部パラメータ (extrinsic parameters) と呼ぶ。

例えば、カメラのレンズはデバイスの一部であるので、カメラの焦点距離といったパラメータは内部パラメータに分類される。一方、カメラの位置や向いている方向といったパラメータは、カメラを操作する人間の意図によって決まるので、外部パラメータに分類される。

さて、三次元の世界がカメラの持つ性質 (内部・外部パラメータ)によって二次元の画像上に映り込むかを決めるわけだが、これをもう少し厳密に定義してみよう。

まず、三次元世界に存在する点が持つ座標を \((X, Y, Z)\) とし、その点が映り込む画像上の位置を \((u, v)\) のように表す。

当然ながら、これらの2点の関係はそれほど単純に書けることばかりではないだろう。しかし、ピンホールカメラという非常に単純化されたカメラモデルを考える場合、これらの2つの点は単純な線形変換によって結びつけられる。

8.1.1. ピンホールカメラ

ピンホールカメラは次の図で表されるような投影機構を持つカメラである。

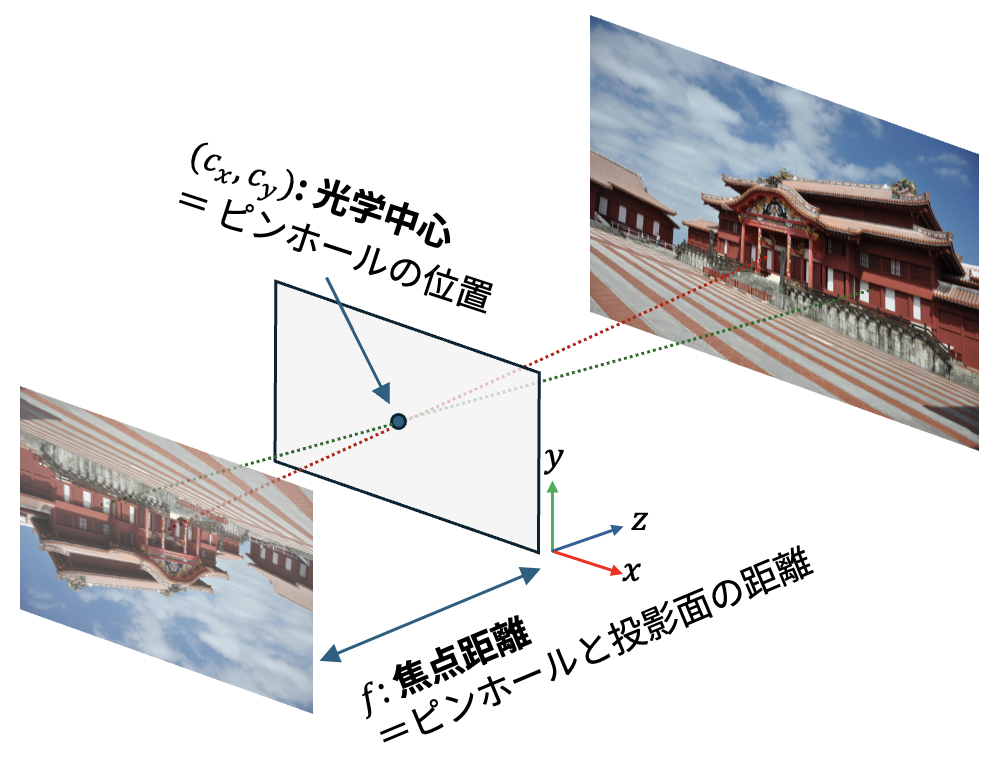
図 8.1 ピンホールカメラの概念図

この概念図では、小さな箱に開けられた穴 (ピンホール)を通して三次元の世界が箱の中に用意された投影面に映り込んでいる。

ピンホールカメラにおいては、ピンホールの位置を 光学中心 と呼び、光学中心から投影面までの距離を 焦点距離 と呼ぶ。以後、光学中心が画像面に映り込む位置を \((c_x, c_y)\) とし、焦点距離を \(f\) と書く。

ここで光学中心を原点とする座標系を考えよう。この座標系では、\(x\) 軸と \(y\) 軸は画像面に平行で、\(z\) 軸は光学中心から画像面に向かい、画像面と垂直に交わるベクトルの方向 (あるいはその逆方向)を指す。

すると、\(X\) と \(u\)、ならびに \(Y\) と \(v\) のそれぞれは

\[\begin{split} \begin{align*} X : (u - c_x) &= Z : f \\ Y : (v - c_x) &= Z : f \end{align*} \end{split}\]

という比例関係を持つことが分かる。従って、以下の関係式が成り立つ。

\[\begin{split} \begin{align*} u &= \frac{f}{Z} X + c_x \\ v &= \frac{f}{Z} Y + c_y \end{align*} \end{split}\]

この式を同次座標系によって行列表現に直すと、次の式が得られる。

\[\begin{split} \begin{pmatrix} u \\ v \\ 1 \end{pmatrix} = \begin{pmatrix} f & 0 & c_x \\ 0 & f & c_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} \end{split}\]

ピンホールカメラモデルでは、この関係式に現れる3×3の行列は 内部行列 (intrinsic matrix) と呼ばれカメラの内部パラメータに対応する。

---

ここまでの議論ではカメラの光学中心を原点とする座標系を考えたが、実際にはカメラの光学中心は三次元世界の原点に存在するとは限らない (座標の定義の仕方による)。また、先ほどの座標系におけるx,y,z 軸の向きも、カメラの向きによって変化する。

そのため内部行列を適用するために、三次元世界の上の点をカメラの光学中心を原点とする座標系に変換する必要がある。この変換を担うのがカメラの外部パラメータである。

通常、カメラの位置を変えることで三次元世界の物体の物理的な大きさが変わったり形が歪んだりすることはないので、外部パラメータは単純な回転行列 \(\mathbf{R}\) と並進ベクトル \(\mathbf{t}\) の組み合わせで表せる。

従って、外部パラメータは3×4の行列として \((\mathbf{R} | \mathbf{t})\) の形で表される。以上をまとめると、カメラの内部・外部パラメータを用いた三次元座標から画像座標への変換は次のように表される。

\[\begin{split} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \mathbf{K} \left( \mathbf{R} | \mathbf{t} \right) \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix} \end{split}\]

この式において行列 \((\mathbf{R} | \mathbf{t})\) はカメラの 外部行列 (extrinsic matrix) と呼ばれ、その内部行列との積 \(\mathbf{K}(\mathbf{R} | \mathbf{t})\) は カメラ行列 (camera matrix) と呼ばれる。

8.1.2. レンズによる画像の歪み

実際のカメラを用いて撮影される画像は、ピンホールカメラのような単純なモデルでは表現できず、最も典型的にはレンズの影響を受けて画像に歪みが生じる。

レンズによる歪みにはレンズの径方向に沿った歪みである 放射歪み (radial distortion) と、レンズの表面に沿った歪みである 接線歪み (tangential distortion) がある。

図 8.2 レンズによる画像歪みの例

放射歪みはレンズの表面が球面であることにより生じる歪みで、画像の中心部が周囲と比較して縮小されたり拡大されたりする (図 8.2 中央)。

具体的には、画素の位置 \((x, y)\) が3つの歪み係数 \(k_1\), \(k_2\), \(k_3\) によって、位置 \((x', y')\) に歪んで投影される。

\[\begin{split} \begin{align*} x' &= x(1 + k_1 r^2 + k_2 r^4 + k_3 r^6) \\ y' &= y(1 + k_1 r^2 + k_2 r^4 + k_3 r^6) \end{align*} \end{split}\]

一方で、接線歪みはレンズが画像平面 (典型的にはイメージセンサ)に対して平行に取り付けられていないことに起因する歪みで、画像が一定の方向に引き伸ばされたような歪みが生じる (図 8.2 右)。

具体的には、画素の位置 \((x, y)\) が2つの歪み係数 \(p_1\), \(p_2\) によって、位置 \((x', y')\) にずれて投影される。

\[\begin{split} \begin{align*} x' &= x + (2p_1xy + p_2(r^2 + 2x^2)) \\ y' &= y + (p_1(r^2 + 2y^2) + 2p_2xy) \\ \end{align*} \end{split}\]

このような歪みは画素の位置を非線形に変化させるので、次に紹介するエピポーラ幾何学において行われる線形変換に基づいたカメラの投影モデルを困難にさせる。

従って、これらの歪みパラメータはカメラごとに キャリブレーション と呼ばれる処理によって校正しておく必要がある。

8.1.3. カメラキャリブレーション

カメラキャリブレーションは、既知の三次元点が投影された際に、画像上にどのように映り込むかを調べることで、カメラのレンズ歪みと内部パラメータを求める処理である。

キャリブレーションには、通常、特徴点の検出が容易なパターン画像を用いることが多く、最も典型的にはチェスボードパターンを用いる。

図 8.3 コーナー点が 5×6 のチェスボードパターン

このようなパターンを平面上に配して、それをキャリブレーションしたいカメラで撮影する。

通常、キャリブレーション用の画像は複数枚撮影される。以下にその一例を示す。

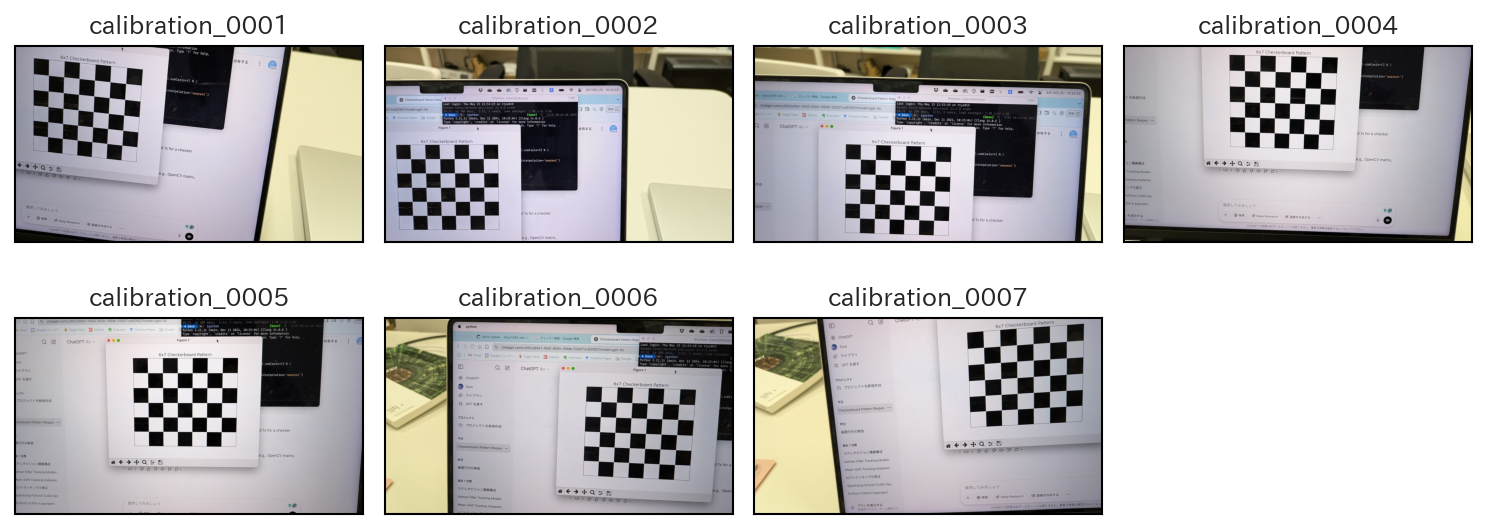
図 8.4 キャリブレーション用画像の撮影例

チェスボード上のコーナー点は、平面上に規則正しく配置されているので、チェスボードのセルの大きさを \(S\) とし、チェスボードがz座標が0のxy平面上に置かれていると考えれば、コーナー点の3次元座標は整数 \(n\), \(m\) を用いて \((nS, mS, 0)\) のように表すことができる。

チェスボードが上手く撮影できていれば、コーナー点の検出は比較的容易で、ある程度の精度でコーナー点の位置を検出することができる。

コーナー点の検出結果を以下に示す。

図 8.5 コーナー点の検出結果

もし使用しているカメラにレンズの歪みがなければ、このパターンは射影変換によって画像上に投影されるので、各コーナー点は画像上でとある直線の上に映ることになる。

しかし、実際のカメラはレンズの歪みを持っているので、コーナー点は画像上で直線上に映るとは限らない。

そこで、実際のコーナー点の位置と、理想的な射影変換によって得られるコーナー点の位置を比較することでレンズの歪みを求める。ここでは詳細を割愛するが、興味のある読者は [31] を参照してほしい。

キャリブレーションが完了すると、カメラの内部行列 \(\mathbf{K}\) と、合計5つの歪み係数 \(\mathbf{d} = (k_1, k_2, p_1, p_2, k_3)\) が得られる。

8.2. エピポーラ幾何学

エピポーラ幾何学 は三次元世界と2つのカメラの関係を記述する幾何学である。

しかし、その説明に入る前に、なぜ2つのカメラを用いることで三次元世界の情報を得ることができるのかを考えてみよう。

ステレオビジョンの基本となる考え方は、三角形の相似関係を用いて距離を測る 三角測量 にある。三角測量を用いると、距離が分かっている点から同じ三次元世界の上の点を見たときの角度を用いてその点までの距離を測ることができる。

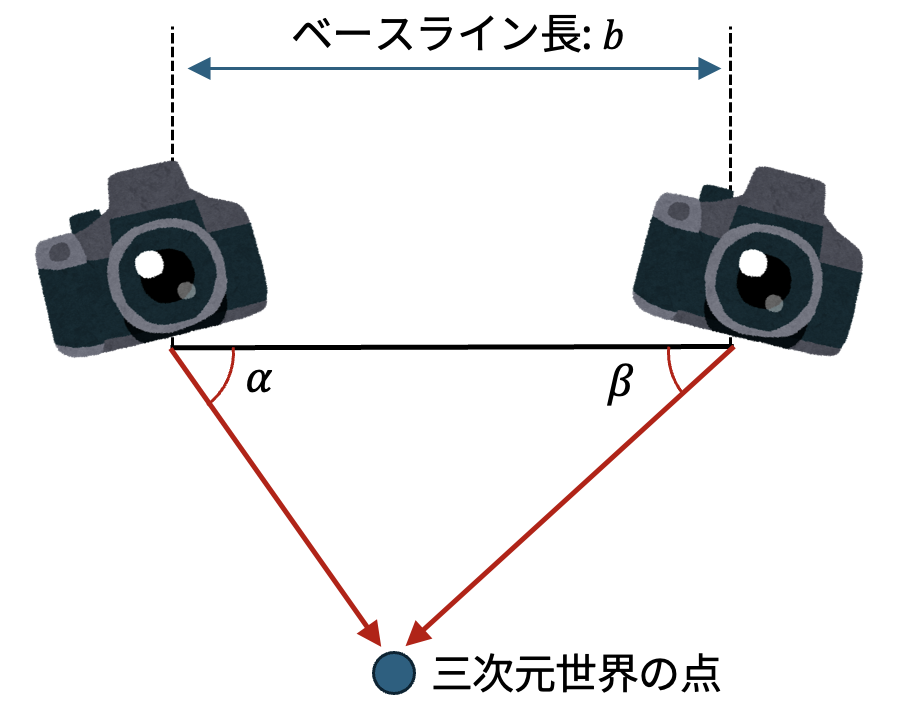
図 8.6 三角測量の概念図

説明は不要かもしれないが、1つの辺の長さと辺の両端の角度が分かると三角形が1つに決まるので、その三角形の底辺から対点までの距離が観測元の二点を結ぶ直線から、観測先の点までの距離と一致する。

ステレオビジョンの条件を三角測量に当てはめると、三角形の既知の1辺の長さは2台のカメラ間の距離である。この距離を ベースライン距離 と呼ぶ。

また、2台のカメラを結ぶ直線に対するカメラの向きが分かっていれば、三次元世界の点が画像上のどの位置に映っているかを調べることで、三角形の既知の2つの角度を求めることができる。

このカメラの向きを決めるのが外部パラメータであり、画像上のどの位置に映るのかを決めるのが内部パラメータである。

従って、2台のカメラのカメラパラメータを用いれば、三角測量の原理から三次元世界の点までの距離を測ることができる。

8.2.1. エピポーラ面とエピポーラ線

ここまでの説明で三角測量を用いれば、2台のカメラを用いて三次元世界の点までの距離を計測できることが分かった。しかし、ここまでの議論はあくまで二次元の三角形の上での話であり、実際には、三次元空間の上で同様の三角形を定義する必要がある。

この三角形の3つの頂点は2台のカメラの光学中心と三次元世界の点である。これらの3点の関係はエピポーラ幾何において以下の図のような関係になっている。この三角形が定義される平面のことを エピポーラ面 (epipolar plane) と呼ぶ。

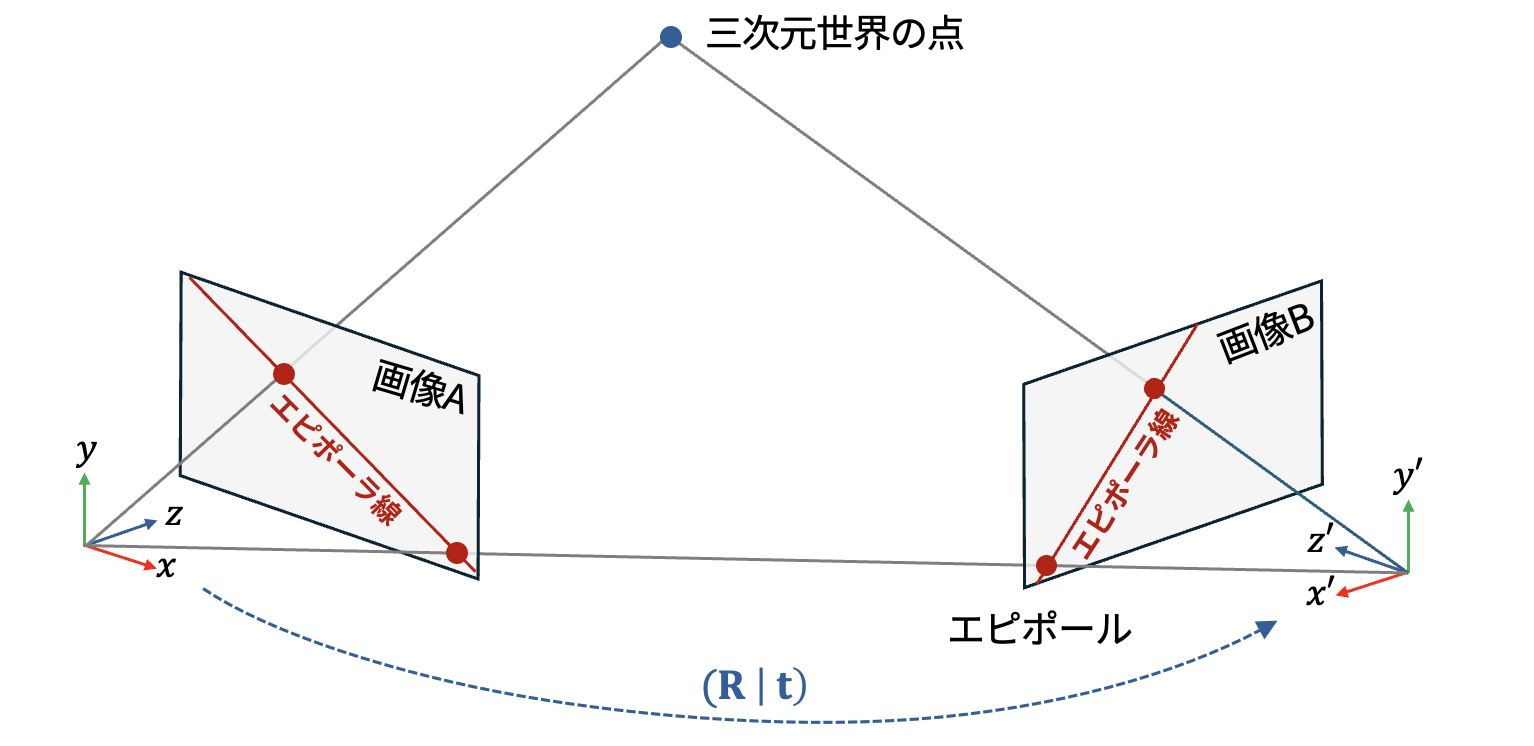
図 8.7 エピポーラ幾何学の概念図

ここでエピポーラ面を別の角度から考えてみると、当然ながら、エピポーラ面上には、2台のカメラの光学中心と距離を求めたい三次元世界の点が存在する。この事実はステレオマッチングにおいて重要な意味を持つ。

ここまで、三次元世界の点が2つのカメラから撮った画像の上で既知であると仮定してきたが、実際には、画像上で三次元世界の同じ点が映っている点を求める必要がある。

今、2枚の画像をA, Bとしたとき、Aの画像上のとある点がBの画像上のどの位置にあるのかを知りたいとしよう。この時、最も単純にはテンプレート・マッチングの要領で、Bの画像上の全ての点についてAの画像上の点との類似度を計算すれば良いのだが、これでは計算量が膨大になってしまう。

しかし、エピポーラ面の性質を考えれば、Aの画像上の点が写している三次元世界の点は、Bの画像平面とエピポーラ面の交差する線上に存在することが分かる。この事実を用いれば、Bの画像上での対応位置の探索を大幅に効率化できる。

このようなエピポーラ面と画像平面との交差領域に現れる直線を エピポーラ線 (epipolar line) と呼ぶ。

ステレオ画像に対していくつかの対応点に対してエピポーラ線を描画してみた結果を以下に示す。

図 8.8 エピポーラ線の描画例

以下では、このようなエピポーラ線がどのような性質の基に定義されるのかを見ていく。

8.2.2. 基礎行列と基本行列

エピポーラ線は、 基礎行列 (fundamental matrix) と呼ばれる行列 \(\mathbf{F}\) を用いて定義される。

2つの画像上での対応点を同次座標を用いて \(\mathbf{u}_a = (u_a, v_a, 1)\) と \(\mathbf{u}_b = (u_b, v_b, 1)\) とする時、以下の関係式が任意の対応点について成り立つ。

(8.1)\[\begin{split} \mathbf{u}_b^\top \mathbf{F} \mathbf{u}_a = \begin{bmatrix} u_b & v_b & 1 \end{bmatrix} \mathbf{F} \begin{bmatrix} u_a \\ v_a \\ 1 \end{bmatrix} = 0 \end{split}\]

この式は エピポーラ拘束式 と呼ばれる。

エピポーラ拘束式において、 \(\mathbf{l} = \mathbf{F} \mathbf{u}_a\) と置くと、\(\mathbf{u}_b^\top \mathbf{l} = 0\) と書き直せ、画像B上での直線に対応する (同様にして画像B上の直線も表せる)。

ここで生じる疑問は このような関係式が任意の対応点に成り立つのはなぜか ということである。

これを理解するには、図 8.7に示した三次元世界における点の位置を表す座標系を考える必要がある。

この図において「画像Aを撮影するカメラの光学中心 \(\mathbf{C}_a\) を原点とする座標系」を「画像Bを撮影するカメラの光学中心 \(\mathbf{C}_b\) を原点とする座標系」に写すには、

• 画像Aの座標系を画像Bの座標系に合うように回転させる

• 画像Aの座標系の原点が画像Bの座標系の原点に一致するように平行移動させる

という2つの変換を行えば良い。

少々分かりづらい部分だが、ここで考えている座標系は画像上の「画素を単位とする座標系」ではなく、カメラの光学中心と向きを基準としつつも三次元世界の物体の大きさを維持した座標系であることに注意してほしい。

このような2つのカメラが持つ座標系の間の変換に用いる回転行列を \(\mathbf{R}\)、平行移動ベクトルを \(\mathbf{t}\) としよう。

ここで、カメラAの座標系における任意の点の座標 \(\mathbf{x}_a = (x_a, y_a, z_a)\) を、カメラBの座標系における座標 \(\mathbf{x}_b = (x_b, y_b, z_b)\) に変換すると次のような関係式が得られる。

\[ \begin{equation} \mathbf{x}_b = \mathbf{R} \mathbf{x}_a + \mathbf{t} \end{equation} \]

警告

\(\mathbf{x}_a\) はカメラAの光学中心 \(\mathbf{C}_a\) を原点とする座標系における三次元世界の点の座標であるのに対し、 \(\mathbf{x}_b\) はカメラBの光学中心 \(\mathbf{C}_b\) を原点とする座標系における三次元世界の点の座標であるという点に注意すること。

ここで、平行移動成分のベクトル \(\mathbf{t} = (t_x, t_y, t_z)\) に対して、外積を取る操作に対応する次のような行列を考える。

\[\begin{split} [\mathbf{t}]_\times = \begin{pmatrix} 0 & -t_z & t_y \\ t_z & 0 & -t_x \\ -t_y & t_x & 0 \end{pmatrix} \end{split}\]

すると、 \(\mathbf{E} = [\mathbf{t}]_\times \mathbf{R}\) と置くことにより、

(8.2)\[ \mathbf{x}_b^\top \mathbf{E} \mathbf{x}_a = 0 \]

が満たされる。実際、\(\mathbf{x}_b\) と \(\mathbf{E}\) に、その定義を代入してみると、

\[\begin{split} \begin{align*} \mathbf{x}_b^\top \mathbf{E} \mathbf{x}_a &= (\mathbf{R} \mathbf{x}_a + \mathbf{t})^\top [\mathbf{t}]_\times \mathbf{R} \mathbf{x}_a \\ &= \left( \mathbf{R} \mathbf{x}_a \right)^\top [\mathbf{t}]_\times \mathbf{R} \mathbf{x}_a + \mathbf{t}^\top [\mathbf{t}]_\times \mathbf{R} \mathbf{x}_a \end{align*} \end{split}\]

と書くことができ、

• \((\mathbf{R} \mathbf{x}_a)^\top\) と \([\mathbf{t}]_\times \mathbf{R} \mathbf{x}_a\) は外積の性質より直交する

• 故にこれらの内積を取ると \((\mathbf{R} \mathbf{x}_a)^\top [\mathbf{t}]_\times \mathbf{R} \mathbf{x}_a = 0\) が成り立つ

• \(\mathbf{t}^\top [\mathbf{t}]_\times\) は \([\mathbf{t}]_\times\) の定義からゼロベクトルに等しい

という性質から、\(\mathbf{x}_b^\top \mathbf{E} \mathbf{x}_a = 0\) が成り立つことが分かる。

(8.2) に現れる行列 \(\mathbf{E}\) を 基本行列 (essential matrix) と呼ぶ。

(8.2) 中の \(\mathbf{x}_a\) と \(\mathbf{x}_b\) に内部行列 \(\mathbf{K}_a\), \(\mathbf{K}_b\) を掛けると \(\mathbf{u}_a = \mathbf{K} \mathbf{x}_a\), \(\mathbf{u}_b = \mathbf{K}_b \mathbf{x}_b\) のように画像上の点のピクセル座標に変換されるのであった。

これらを (8.2) に代入すると、画像A, 画像B上における対応点のピクセル座標 \(\mathbf{u}_a\), \(\mathbf{u}_b\) について以下の関係式が成り立つ。

\[\begin{split} \begin{align*} (\mathbf{K}_{b}^{-1} \mathbf{u}_b)^\top \mathbf{E} (\mathbf{K}_a^{-1} \mathbf{u}_a) \\ \mathbf{u}_b^\top \left( \mathbf{K}_b^{-\top} \mathbf{E} \mathbf{K}_a^{-1} \right) \mathbf{u}_a = 0 \end{align*} \end{split}\]

従って、

\[ \mathbf{F} = \mathbf{K}_b^{-\top} \mathbf{E} \mathbf{K}_a^{-1} \]

のように基礎行列を定義すれば、任意の対応点の間で (8.1) に示したエピポーラ拘束式が成り立つことが分かる。

8.2.3. 基本行列の計算

キャリブレーション済みのカメラによって撮影された2枚の画像から基本行列を求めるには、まず、2枚の画像上の対応する点を求める必要がある。

この目的には 画像特徴量 で紹介したSIFT等の特徴点抽出器を用いることができる。以下にSIFTによる対応点検出の結果を示す。

図 8.9 SIFT特徴量のマッチング結果

このようにして得られた対応点に番号をつけて、 \((\mathbf{u}_{a,i}, \mathbf{u}_{b,i})\) のように表すことにする。

今、カメラはキャリブレーション済みであるので、内部行列 \(\mathbf{K}\) が分かっている。従って、この逆行列を作用させることで、カメラA, Bの光学中心を原点とするカメラ座標系での位置が求められる。

これを \((\mathbf{x}_{a,i}\), \(\mathbf{x}_{b,i})\) のように書くことにすると、

\[\begin{split} \begin{align*} \mathbf{x}_{a,i} &= \mathbf{K}^{-1} \mathbf{u}_{a,i} \\ \mathbf{x}_{b,i} &= \mathbf{K}^{-1} \mathbf{u}_{b,i} \end{align*} \end{split}\]

が成り立つ。

ここで得られるカメラ座標における位置 \(\mathbf{x}_{a,i}\), \(\mathbf{x}_{b,i}\) は スケールに対する不確定性を持つ。

つまり、実際に観測している三次元世界の点 \(\mathbf{x}\) が適当なスケール \(\lambda_a\), \(\lambda_b\) を用いて \(\mathbf{x} = \lambda_a \mathbf{x}_{a,i} = \lambda_b \mathbf{x}_{b,i}\) と表せることまでは分かっているが、肝心のスケール \(\lambda_a, \lambda_b\) までは分からない。

警告

\(\mathbf{K}\) は3x3の行列で、\(\mathbf{u}_{a,i}\) や \(\mathbf{u}_{b,i}\) は同次座標系で表されているため、変換の過程でスケールの成分がキャンセルされてしまうから。

しかしながら、 (8.2) の拘束式は任意のスケール \(\lambda_a, \lambda_b\) に対して成り立つので、スケールの不確定性は基本行列を求めるうえでは問題にならない。

故に、単純な逆投影操作によって得られた任意の座標のペア \((\mathbf{x}_{a,i}, \mathbf{x}_{b,i})\) に対して、

\[ \mathbf{x}_{b,i}^\top \mathbf{E} \mathbf{x}_{a,i} = 0 \]

が成り立つように基本行列 \(\mathbf{E}\) を求めれば良い。

ここで、\(\mathbf{E}\) が回転行列 \(\mathbf{R}\) と平行移動ベクトル \(\mathbf{t}\) を用いて表せることを思い出してほしい。

回転行列 \(\mathbf{R}\) は各軸周りの回転により定義できるので自由度は3, 平行移動ベクトル \(\mathbf{t}\) は、現在、方向のみが重要で長さは任意で良いので、自由度は2である。

以上から、基本行列の自由度は5しかなく、対応点が5組以上あれば、最小二乗法等の手法を用いて基本行列を求めることができる。

ただし、SIFT等を用いた特徴点マッチングの結果、誤った点の対応関係が得られる可能性があるという点には注意が必要である。

このような間違った対応点を含む場合には、 RANSAC (random sample consensus) と呼ばれる手法が用いられることが多い。

RANSACを基本行列の計算に適用する場合、対応点の中からランダムに5つの点を選んで基本行列を求めて、すべての対応点の中から外れ値と思われる点のペアを除外する。

このような基本行列の計算と外れ値の除外を繰り返すことで、最終的にもっともらしい基本行列を求めることができる。

8.2.4. 外部パラメータの復元

ここまでの過程で、基本行列 \(\mathbf{E}\) を求めることができた。

基本行列 \(\mathbf{E}\) は、カメラAとカメラBの間の相対的な位置関係を表す外部パラメータである回転行列 \(\mathbf{R}\) と平行移動ベクトル \(\mathbf{t}\) を用いて表されるのであった。

しかし、基本行列をRANSAC等で求める過程では、回転行列 \(\mathbf{R}\) と平行移動ベクトル \(\mathbf{t}\) を陽に考えてはいないので、基本行列を求めたあとに、これらの外部パラメータを復元する必要がある。

この復元の過程は、

• 基本行列 \(\mathbf{E}\) のランクが2である

• 回転行列は直交行列で表される

という点に注意すると、特異値分解によって復元できる。

ここで、基本行列 \(\mathbf{E}\) の特異値分解を

\[ \mathbf{E} = \mathbf{U} \boldsymbol\Sigma \mathbf{V}^\top \]

と表す。

この時、\(\mathbf{R}\) は直交行列ですべての特異値が1, \([\mathbf{t}]_\times\) は、その定義から、特異値が \((\| \mathbf{t} \|, \| \mathbf{t} \|, 0)\) である。

故に、基本行列がスケールの不定性を持っていることを思い出すと、

\[\begin{split} \boldsymbol\Sigma = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix} \end{split}\]

としても問題ない。また、

\[ \mathbf{U} = [\mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3] \]

のように書くと外積の性質から、

\[ [\mathbf{u}_3]_\times \mathbf{U} = [\mathbf{u}_2, -\mathbf{u}_1, \mathbf{0}] = \mathbf{Z} \mathbf{U} \]

が成り立つ。ただし、

\[\begin{split} \mathbf{Z} = \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \end{split}\]

である。従って、

\[\begin{split} \mathbf{W} = \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{split}\]

のように書くことで、基本行列 \(\mathbf{E}\) を以下のように書き直せる。

\[\begin{split} \begin{align*} \mathbf{E} &= \mathbf{U} \boldsymbol\Sigma \mathbf{V}^\top \\ &= \mathbf{U} \mathbf{Z} \mathbf{W} \mathbf{V}^\top \\ &= [\mathbf{u}_3]_\times \mathbf{U} \mathbf{W} \mathbf{V}^\top \end{align*} \end{split}\]

この式において \(\mathbf{U} \mathbf{W} \mathbf{V}^\top\) の部分は直交行列なので、これを回転行列に対応させると、基本行列 \(\mathbf{E}\) は次の \(\mathbf{R}\) と平行移動ベクトル \(\mathbf{t}\) に分解できる。

\[ \begin{align*} \mathbf{R} &= \mathbf{U} \mathbf{W} \mathbf{V}^\top \mathbf{t} &= \mathbf{u}_3 \end{align*} \]

ただし、実際には、\(\mathbf{t}\) を \(\mathbf{u}_3\) と \(-\mathbf{u}_3\) のどちらに対応させるか、\(\mathbf{W}\) の (3, 3)成分の符号が正か負かという曖昧さがあり、

\[\begin{split} \begin{align*} \mathbf{R}_1 &= \mathbf{U} \mathbf{W} \mathbf{V}^\top \\ \mathbf{R}_2 &= \mathbf{U} \mathbf{W}^\top \mathbf{V}^\top \end{align*} \end{split}\]

とおいて、 \((\mathbf{R}_1, \pm \mathbf{t})\) と \((\mathbf{R}_2, \pm \mathbf{t})\) の4つの選択肢が考えられる。

この4つから、現在、得られている対応点の座標がすべて正のz座標を持つものを選ぶと、適切な外部パラメータ \((\mathbf{R}, \mathbf{t})\) が得られる。

8.3. ステレオマッチング

ステレオマッチング とは、1組のステレオ画像に対して、同じ三次元世界の点の密な対応関係を求める手法を指す。

ここまでの議論でエピポーラ線を求めることができれば、その直線上を探索することで効率的に同じ三次元世界の点を写す対応点を求められることが分かった。

しかし、エピポーラ線は通常、画像の上で斜めに走っており、また処理したい対応点ごとに向きも異なるため計算処理が複雑になりやすい。

そのため、ステレオマッチングのアルゴリズムは、計算量の削減の観点から、入力されるステレオ画像において、同一の三次元世界の点が同じy座標を持つことを前提にして設計されている。

対応点が同じy座標を持つ、ということはエピポーラ線が水平であり、2つの画像上で同じy座標を持つことと同義である。

このようにエピポーラ線が水平になるように画像を変換する処理を ステレオ平行化 (stereo rectification) と呼ぶ。

8.3.1. ステレオ平行化

ステレオ平行化の処理を数学的に記述するには、まず、エピポーラ線の定義について考える必要がある。

エピポーラ面が2つのカメラの光学中心を含む平面であることを考えると、エピポーラ線は、画像Aの光学中心の画像B上での位置を通る。このような他方のカメラの光学中心の位置を エピポール (epipole) と呼ぶ。

エピポーラ線は必ずエピポールを通るので、エピポーラ線が全て平行になる、という状況は、エピポールが画像の右あるいは左の無限遠点にある、ということを意味する。このような状況になるのは2台のカメラの画像平面が同一平面上に存在する場合だけである。

従って、平行化のためには、各画像を撮影するカメラが持つ座標系を回転させて、互いに平行移動の関係にある座標系になるように変換すれば良い。

具体的には、

• x軸がベースライン線と同じ向き

• z軸は任意の視点方向 (通常はカメラAかカメラBの向きのいずれか、あるいはその平均)

• y軸はz軸とx軸の外積

となるように共通の座標系を定義して、その向きに合うように画像A, Bの座標系を回転させれば良い。

ここまでの内容で、2台のカメラの間の相対的な位置関係が回転行列 \(\mathbf{R}\) と平行移動ベクトル \(\mathbf{t}\) によって記述されているので、このような平行化のための回転行列の導出はそれほど難しくないだろう。

このようにして平行化のための各カメラに対する回転行列 \(\mathbf{R}_a\), \(\mathbf{R}_b\) が求まったら、カメラの内部行列 \(\mathbf{K}\) を用いて

\[\begin{split} \begin{align*} \mathbf{u}_{a, \text{new}} = \mathbf{K} \mathbf{R}_a \mathbf{K}^{-1} \mathbf{u}_a \\ \mathbf{u}_{b, \text{new}} = \mathbf{K} \mathbf{R}_b \mathbf{K}^{-1} \mathbf{u}_b \end{align*} \end{split}\]

のような変換を用いて画像をリサンプリングすることで、平行化後の画像を得ることができる。

以下に、平行化後の画像の例を示す。

図 8.10 平行化済みの画像

8.3.2. 視差と深度の復元

画像が平行化できたら、実際のステレオマッチングの処理に入る。

最も単純なステレオマッチングのアルゴリズムには ブロックマッチング法 があり、これは画像Aのある画素に対して、画像Bの同じy座標を持つ画素の周囲の領域を探索して、最も類似度が高い画素を探すという方法である。

すると、画像Aと画像Bの間で、同じ三次元世界の点を写す点が どれだけずれて写っているか が分かる。このずれの量のことを 視差 (disparity) と呼ぶ。

上記の平衡化済み画像に対して視差計算を行った結果を以下に示す (以下は単純なブロックマッチング方ではなく、セミグローバル法という方法で計算されている)。

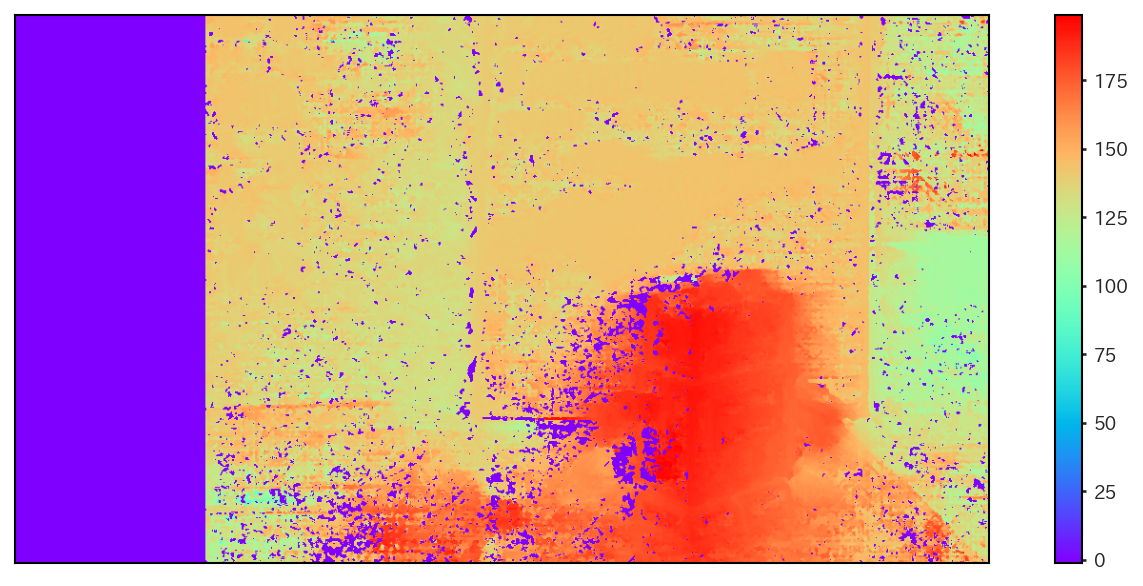
図 8.11 視差画像

ステレオ画像を撮影している2台のカメラの相対位置が既知である場合、視差の情報をカメラからの距離の情報に置き換えることができる。

このカメラからの距離のことを 深度 (depth) と呼び、各画素に深度が記録された画像を特に 深度画像 と呼ぶ。

通常、カメラに対して近くにあるものほど視差が大きく、逆に遠くにあるものほど視差が小さくなる。

この関係は反比例の式で表すことができ、とある画素の視差を \(d\)、カメラからの距離を \(z\) とすると、以下の関係式が成り立つ。

\[ d = \frac{f \cdot b}{z} \]

ここで、\(f\) はカメラの焦点距離、\(b\) は2台のカメラの間のベースライン距離である。

今回のように1台のカメラで2枚の画像を撮影した場合には、画像だけから正確なベースライン距離を知ることはできないので、正確な深度画像は求められない。

それでも、画像内に映るシーンの形状を知るためには十分で、上記の視差画像から深度画像を求め、その結果を基に三次元上に点を描画すると、次のような結果が得られる。

以上のように、カメラをキャリブレーションしておけば、同一のカメラから得られる2枚の画像によって、実世界の三次元情報を復元することができる。

今回は画像を2枚だけ用いたが、3枚以上の画像を用いるとさらなる精度向上が可能で、このような多数の画像からの三次元復元は 多視点ステレオ (multi-view stereo) として広く研究されている。