演習: 物体追跡とステレオビジョン

4. 演習: 物体追跡とステレオビジョン#

4.1. はじめに#

レポートはテンプレートファイルを使用して作成してください。また、ファイル名は 「(7桁の学籍番号)_第x回_画像処理レポート.docx」 (xの部分は何回目の課題なのかを記入)に変更してください。

課題作成上の注意

課題を作成する際には、プログラムは別に .py ファイルで作成して、本レポートと一緒に圧縮したうえで提出してください。また、Jupyter Notebook形式のファイル (拡張子が.ipynb)のものは受け付けません。

加えて、プログラムを添付したのみで内容に関する説明や結果に関する考察のないもの、単なる結果の羅列になっているもの(またはそのように見えるもの)は採点しませんのでご注意ください。

4.1.1. Lucas-Kanade法の実装#

まずは、各自でオプティカル・フローの検出を行う動画を撮影しよう (長くても3秒くらいの動画にすること)。

動画が撮影できたら、適当なウェブサイト等を使って動画を連番画像に変換しておく (video to image sequence などと検索すると良い)。

それを適当なフォルダに画像を格納して、OpenCVから画像を読み込み、簡単のためにグレースケールかつ浮動小数での表現に変換しておく。

import cv2
import numpy as np

img1 = cv2.imread("data/robot/frames_0001.jpg", cv2.IMREAD_COLOR)
img2 = cv2.imread("data/robot/frames_0002.jpg", cv2.IMREAD_COLOR)

gray1 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
gray1 = (gray1 / 255.0).astype(np.float32)
gray2 = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
gray2 = (gray2 / 255.0).astype(np.float32)

画像が読み込めたら、オプティカル・フローの拘束方程式に現れる \(I_x\)、\(I_y\)、\(I_t\) を計算する。これれは単純に\(x\), \(y\), \(t\) の各方向に沿った勾配を計算するだけで良い。

なお、\(x\), \(y\) の勾配については、ノイズの影響を低減するためにSobelフィルタを使用して計算するのが良いだろう。

I_x = cv2.Sobel(gray1, -1, 1, 0, ksize=3)
I_y = cv2.Sobel(gray1, -1, 0, 1, ksize=3)
I_t = gray2 - gray1

ここで、とある点 \((x, y)\) におけるオプティカル・フローを計算しよう。

まずは \((x, y)\) の周囲の画素を取り出す。

w_size = 11 // 2  # 11x11の領域を取り出す
x, y = 100, 100  # オプティカル・フローを求める画素

I_x_w = I_x[y - w_size : y + w_size + 1, x - w_size : x + w_size + 1]
I_y_w = I_y[y - w_size : y + w_size + 1, x - w_size : x + w_size + 1]
I_t_w = I_t[y - w_size : y + w_size + 1, x - w_size : x + w_size + 1]

周辺の画素について \(I_x\), \(I_y\)、\(I_t\) の値が取り出せたら、これらの画素が共通のフロー \((u, v)\) を持つと仮定して、拘束方程式を定義する。

# 方程式を定義
I_x_w = I_x_w.reshape((-1, 1))
I_y_w = I_y_w.reshape((-1, 1))
I_t_w = I_t_w.reshape((-1, 1))

AA = np.concatenate((I_x_w, I_y_w), axis=1)
bb = I_t_w

AA_t_AA = AA.T @ AA
AA_t_bb = AA.T @ bb

あとは得られた連立方程式 \(\mathbf{A}^\top \mathbf{A} \mathbf{x} = -\mathbf{A}^\top \mathbf{b}\) を解けば良いのだが、行列 \(\mathbf{A}^\top \mathbf{A}\) が逆行列を持たないケースも存在するため、小さな値を対角成分に持つ対角行列を足し算して、必ず解がもとまるようにしておく。

この操作は、以下の損失関数を最小化する問題を解くことと同義である。

\[ \min_{u, v} \sum_{i=1}^N \left( I_x u + I_y v + I_t \right)^2 + \lambda \left( u^2 + v^2 \right) \]

ここで、\(\lambda\) は正則化項の重みを表すパラメータである。

# 小さな値を足し算
lmbda = 1.0e-6
AA_t_AA += lmbda * np.eye(2)

# 線形問題を解く
uv = np.linalg.solve(AA_t_AA, -AA_t_bb)

同様の操作を一定の間隔でサンプルされた画素に対して行ったら、得られたフローを可視化してみよう。

フローの可視化には、OpenCVの cv2.arrowedLine を使用すると良いだろう。以下のプログラムでは変数 uvs がフローベクトルを要素に持つ配列として定義されている。

以上の処理を連続する2枚の画像全てに対して行って、結果を可視化してみよう。その上で、Lucas-Kanade法のオプティカル・フロー検出の精度を確認してみると良い。

4.1.2. ステレオマッチングによる三次元復元#

ステレオビジョンで紹介したステレオマッチングによる三次元復元を行うには、

カメラ・キャリブレーション
基本行列の計算とステレオ平行化
ステレオマッチング

の3つのステップを経る必要がある。

カメラ・キャリブレーション#

まずは、ステレオマッチングのための画像を用意しよう。

以下の画像を各自のコンピュータにダウンロードして、画面に表示したうえでキャリブレーション用の写真を数枚撮影する。

../_images/e92d694a134ac57cda7568c10de8fc7277361abb2cf19b7834423b3bcea4283f.png — 図 4.5 キャリブレーションに用いるチェスボード画像#

なお、上記の画像は、内部のコーナー点が5x6個のチェスボードパターンなので注意すること。

撮影が完了したら、適当なフォルダ (以下では stereo) に calibration_0001.jpg 等の名前をつけて保存しておく。

データが用意できたら以下のキャリブレーション用のプログラムを実行して、カメラの内部パラメータとレンズの歪み係数を求めておく。

from pathlib import Path

import cv2
import numpy as np

# キャリブレーションのパラメータ
data_root = Path("data", "stereo")
pattern_size = (5, 6)  # チェスボードのコーナー数 (行, 列)
n_calib_images = 7  # キャリブレーション画像の枚数

# チェスボードのコーナー点の3次元座標
obj_corners = np.zeros((pattern_size[1] * pattern_size[0], 3), np.float32)
obj_corners[:, :2] = np.indices(pattern_size).T.reshape((-1, 2))

# キャリブレーション用画像の読み込み
files = [data_root / f"calibration_{i:04d}.jpg" for i in range(1, n_calib_images + 1)]
images = [cv2.imread(str(f), cv2.IMREAD_COLOR) for f in files]
grays = [cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) for img in images]

# コーナー点の検出
obj_points = []
img_points = []
results = []
for i, img in enumerate(grays):
    # コーナー点を荒く検出
    success, img_corners = cv2.findChessboardCorners(img, pattern_size)

    # 検出に成功したら精度を高める
    if success:
        img_corners2 = cv2.cornerSubPix(
            img,
            img_corners,
            (11, 11),
            (-1, -1),
            (cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_MAX_ITER, 20, 1e-4),
        )

        # 対応する点の座標を保存
        obj_points.append(obj_corners)
        img_points.append(img_corners2)

        # 結果の確認
        res = images[i].copy()
        cv2.drawChessboardCorners(res, pattern_size, img_corners2, success)
        results.append(res)
    else:
        print(f"Chessboard corners not found in image {i + 1}")


# キャリブレーション
### cv2.CALIB_FIX_ASPECT_RATIO を指定して画素のアスペクト比を固定
### cv2.CALIB_ZERO_TANGENT_DIST を指定して接線歪みを無視
height, width = images[0].shape[:2]
rms, K, dist, _, _ = cv2.calibrateCamera(
    obj_points,
    img_points,
    (width, height),
    np.empty(0),
    np.empty(0),
    flags=cv2.CALIB_FIX_ASPECT_RATIO | cv2.CALIB_ZERO_TANGENT_DIST,
)
dist = dist.flatten()

# 結果の確認
print(f"再投影誤差:\n{rms:.6f} [px]")
print("内部行列:\n", K)
print("歪み係数:\n", dist)

再投影誤差:
0.176770 [px]
内部行列:
 [[790.95697144   0.         496.86736813]
 [  0.         790.95697144 298.60417252]
 [  0.           0.           1.        ]]
歪み係数:
 [ 0.08249897 -0.3386506   0.          0.          0.38662893]

正しく計算ができている場合、通常のカメラであれば、再投影誤差は1px以下になる。

また、内部行列中の焦点距離 \(f\) は画像の高さと幅の平均の値、光学中心の位置 \((c_x, c_y)\) は幅と高さの半分程度の値になるはずである。

歪み係数については、どのくらい広角で撮影したかによって大きさが変わるため、一概には言いづらいが、一般的にそれほど大きな値が現れることはない。

基本行列の計算とステレオ平行化#

キャリブレーションによって、内部行列と歪み係数が求まったら、ステレオ画像に対して基本行列を計算する。

まずは、各自でステレオ画像を用意しよう。

各画像は以下で平行化するので、同じシーンを撮影していれば、カメラの姿勢が多少変化しても問題ないが、もし以後の処理で失敗する場合には、背景に何かがが映り込んでいるようなシーンを撮影すると、特徴点のマッチングが上手く行きやすい。

撮影した画像を先ほどと同様に適当なフォルダ (以下では stereo) に xxxx_l.jpg, xxxx_r.jpg 等の名前をつけて保存しておく。

画像が撮影できたら、これら2枚の画像からSIFT特徴を検出して対応点を求める。

各画像から cv2.SIFT.create() で得られる特徴量検出器によって特徴量を検出したら、 cv2.BFMatcher (brute-force matcherの略)を使用して特徴点のマッチングを行う。

以下のプログラムでは knnMatch に k=2 を指定して、1枚目の画像上の特徴点に対して、2枚目の画像上で2番目に近い特徴点までを求めている。

その後、マッチングの精度を上げるために、1番目と2番目の距離の比が0.7以下のものだけを good_matches に残している (特徴点が正確にマッチすれば、1番近い点までの距離はほぼ0であると想定)。

# 画像の読み込み
img1 = cv2.imread(str(data_root / "robot_l.jpg"), cv2.IMREAD_COLOR)
img2 = cv2.imread(str(data_root / "robot_r.jpg"), cv2.IMREAD_COLOR)

# 特徴点の検出
sift = cv2.SIFT.create()
kp1, desc1 = sift.detectAndCompute(img1, np.empty(0))
kp2, desc2 = sift.detectAndCompute(img2, np.empty(0))

# 特徴点のマッチング
matcher = cv2.BFMatcher(cv2.NORM_L2)
matches = matcher.knnMatch(desc1, desc2, k=2)
good_matches = [m for m, n in matches if m.distance < 0.7 * n.distance]

# 信頼度の高いマッチング点を抽出
pts1 = [kp1[m.queryIdx].pt for m in good_matches]
pts2 = [kp2[m.trainIdx].pt for m in good_matches]
pts1 = np.array(pts1, dtype=np.float32)
pts2 = np.array(pts2, dtype=np.float32)

このようにして、ある程度正確な特徴点のペアが求まったら、これらを使って基本行列を計算する。

基本行列の計算には各カメラの光学中心を原点とするカメラ座標系における点の座標を求める必要があるのだった。

撮影に用いているカメラにはレンズの歪みが含まれるはずなので、そのようなケースに対してもカメラ座標系への変換が可能な cv2.undistortPoints を使用する。この関数は、カメラの内部行列と歪み係数を引数にとり、画像上の点をカメラ座標系に変換してくれる。

# マッチング点をカメラ座標系に変換
pts1c = cv2.undistortPoints(pts1, K, dist)
pts2c = cv2.undistortPoints(pts2, K, dist)

カメラ座標に変換した対応点の位置を cv2.findFundamentalMat に渡すと、基本行列が計算できる。

以下のコードでは、基本行列を求めるアルゴリズムにRANSACを使用している。

引数にある prob は、出力の基本行列が満たすべき信頼度を表していて、1に近いほど、より多くの点がエピポーラ拘束式を満たす必要がある (故に計算時間が長くなる)。一方、threshold は、エピポーラ拘束式を満たすとみなすための距離の閾値を表している。

cv2.findFundamentalMat の戻り値は、基本行列と、RANSACによって選ばれた正しい対応点のインデックスであり、以後の点では、正しい対応点だけを用いるように対応点の座標をフィルタリングしておく。

# 基本行列の計算
E, mask = cv2.findEssentialMat(
    pts1c,
    pts2c,
    np.eye(3),
    method=cv2.RANSAC,
    prob=0.999,
    threshold=1.0e-4,
)

# 対応点をフィルタリング
pts1c = pts1c[mask.ravel() == 1]
pts2c = pts2c[mask.ravel() == 1]

基本行列が計算できたら次は、外部行列を計算して、画像を平衡化する。

基本行列を外部行列に分解するには cv2.recoverPose を、平行化のための回転行列を求めるには cv2.stereoRectify を使用する。

# 外部行列の復元
_, R, t, _ = cv2.recoverPose(E, pts1c, pts2c)

# 平行化のための行列を求める
R1, R2, P1, P2, Q, _, _ = cv2.stereoRectify(K, dist, K, dist, (width, height), R, t, alpha=0)

cv2.stereoRectify の戻り値は、平行化のための回転行列 (R1, R2) と、1枚目のカメラに対するカメラ座標系で表された点を2台のカメラそれぞれの画像平面に射影するための投影行列 (P1, P2)、そして、視差画像を深度画像に変換する行列 Q である。

これらの戻り値を用いると、平行化前後の画素の対応関係を cv2.initUndistortRectifyMap を使用して求めることができる。この関数は、対応する平行化後の画像上の画素 \((x, y)\) に対する平行化前の画素の位置 \((x'(x, y), y'(x, y))\) を map1x と map1y に格納してくれるので、これを cv2.remap に渡して平行化後の画像を得る。

# 平行化前後の画素の対応関係を求める
map1x, map1y = cv2.initUndistortRectifyMap(K, dist, R1, P1, (width, height), cv2.CV_16SC2)
map2x, map2y = cv2.initUndistortRectifyMap(K, dist, R2, P2, (width, height), cv2.CV_16SC2)

# 平行化
img1_rect = cv2.remap(img1, map1x, map1y, cv2.INTER_LINEAR)
img2_rect = cv2.remap(img2, map2x, map2y, cv2.INTER_LINEAR)

../_images/9f9fbac4d7637ff53abef623532e1e89508fb448ea103229228d8607f24bc7aa.png

以上で、画像の平行化は完了なので、次のステレオマッチングのために得られた画像を保存しておこう。

ステレオマッチング#

画像が平行化できたら、その画像を入力にしてステレオマッチングを行う。

OpenCVには、ステレオマッチングのためのクラスがいくつか用意されていて、単純なブロックマッチングを行う cv2.StereoBM とセミ・グローバル法を用いる cv2.StereoSGBM がある。

これらのクラスはファクトリメソッドである create を用いてインスタンスを得ることができる。

いずれのクラスもファクトリメソッドの引数に minDisparity と numDisparities を指定する必要がある。

ここで minDisparity は、視差画像の最小値を表していて、通常は0を指定すれば良い。また、名前が少々紛らわしいが numDisparities は、視差の最大値を表す。numDisparities は平行化された画像を見て、一番カメラに近い箇所がどの程度の視差を持つかを見て設定するのが良いだろう。

視差画像が得られたら、stereoRectify の戻り値である Q を用いて、視差画像を深度画像に変換する。この変換には、単純に cv2.reprojectImageTo3D を使用すれば良い。

import cv2
import numpy as np

# セミグローバル法による視差画像の計算
stereo = cv2.StereoSGBM.create(
    minDisparity=0,
    numDisparities=224,
    blockSize=1,
    P1=1,
    P2=1000,
)

# 視差画像の正規化
disp = stereo.compute(img1_rect, img2_rect).astype(np.float32)
disp = disp / 16.0  # SGBMの出力は視差が16倍されている
disp[disp <= 0] = 0.0

# 深度画像の計算
depth = cv2.reprojectImageTo3D(disp, Q)
depth[disp <= 0] = 0.0

以上の処理を経て得られた視差画像と深度画像を以下に示す。

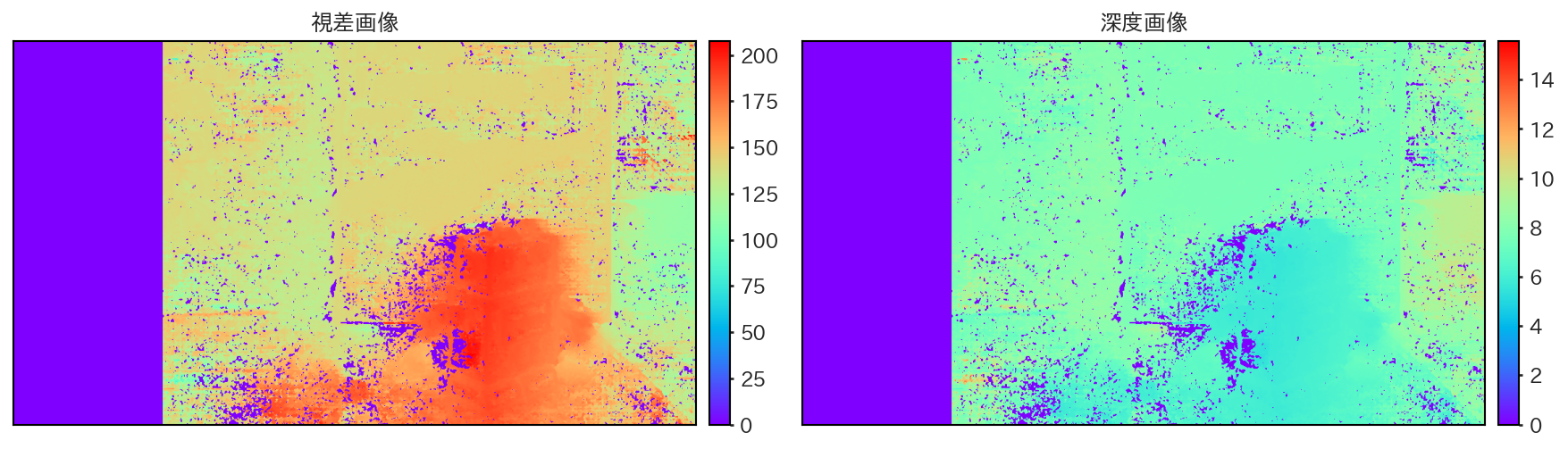
../_images/a14677bf70e8db98334f323cac77f348259231751569fa44fbfa736624118a48.png

深度画像が得られたら、画素の位置 \((x, y)\) と、深度 \(z(x, y)\) を用いて、全ての有効画素 (視差 disp が0より大きい画素) を三次元空間の点 \((x, y, z)\) に変換する。

このような点群データはWavefront OBJ (*.obj) やStanford PLY (*.ply) 形式で保存することで他のプログラムで表示できる。

以下はPLY形式での保存を行うプログラムである。

import numpy as np
from plyfile import PlyData, PlyElement

# 三次元点群の作成
depth = depth.reshape(-1, 3)
depth = depth[disp.ravel() > 0.0]
xs, ys, zs = depth[:, 0], depth[:, 1], depth[:, 2]
xyz = np.stack((xs, ys, zs), axis=1)
rgb = img1_rect.reshape(-1, 3)
rgb = rgb[disp.ravel() > 0.0]
rgb = rgb[:, ::-1]

# PLYファイルとして保存
ply_name = "points.ply"
n_points = xs.shape[0]
vertex = np.empty(
    n_points,
    dtype=[
        ("x", "f4"),
        ("y", "f4"),
        ("z", "f4"),
        ("red", "u1"),
        ("green", "u1"),
        ("blue", "u1"),
    ],
)
vertex["x"] = xyz[:, 0].astype(np.float32)
vertex["y"] = xyz[:, 1].astype(np.float32)
vertex["z"] = xyz[:, 2].astype(np.float32)
vertex["red"] = rgb[:, 0].astype(np.uint8)
vertex["green"] = rgb[:, 1].astype(np.uint8)
vertex["blue"] = rgb[:, 2].astype(np.uint8)

element = PlyElement.describe(vertex, "vertex")
ply = PlyData([element], text=False)
ply.write(ply_name)

作成されたPLYファイルは MeshLab や CloudCompare などの他、 vscode-3d-previewなどの拡張を入れればVSCode上でも表示することができる。

4.2. 演習問題#

問題1

Lucas-Kanade法によるオプティカル・フローの計算

各自で撮影した動画を用いて、Lucas-Kanade法に用いて、オプティカル・フローを計算し、その結果を可視化せよ。また、結果からLucas-Kanade法の性質について考察しなさい。

なお、OpenCVには cv2.calcOpticalFlowPyrLK という関数が用意されているが、これを使用してはならない。

問題2

カメラキャリブレーション

本節で示したプログラムを参考にして、各自でキャリブレーション用画像を撮影し、カメラの内部パラメータとレンズの歪み係数を求めよ。得られた内部行列と歪み係数は *.npy ファイル等に保存しておくこと。

問題3

ステレオ平行化

各自でステレオ画像を撮影し、SIFT特徴量による対応点の検出、基本行列の計算、ならびにステレオ平行化を実行せよ。平行化された画像はステレオマッチングのために別ファイルとして保存しておくこと。

問題4

ステレオマッチング

前問で得られた平行化済みの画像を用いてステレオマッチングを行い、視差画像を計算せよ。その後、平行化時に求めた逆投影行列 Q を用いて深度画像に変換しなさい。

得られた深度画像から、三次元点群を作成し、PLYファイルとして保存後、MeshLab等で正しい結果が得られているかを確認すること。

これらの作業を通して、2枚の画像だけを用いたステレオマッチングの性能について考察しなさい。